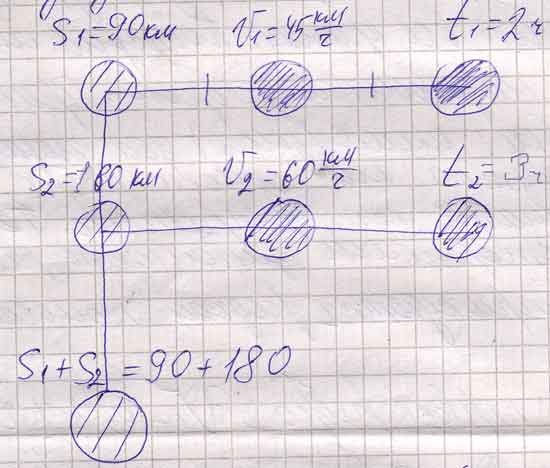Семинар ДООМ. Графы: решение задач на составление уравнений
Команды
Тема «Решение задач с помощью графов» рассчитана на 8 часов.
Цель:
- овладеть новым эффективным способом решения текстовых задач на «движение», «стоимость», «совместную работу», «заполнение резервуара водой» и т. д – способом решения текстовых задач – сетевым графом;
- научить составлять уравнение по условию задачи, описывать выбор переменных уравнения; составлять и обосновывать выбор ответа.
Задачи:
- Приобщить учеников к работе с математической литературой;
- Научить составлять математическую модель текстовой задачи, переходить от этой модели к ответам задачи, анализируя жизненную ситуацию текста задачи.
Урок 1.Тема «Решение задач на составление уравнений»
Любая задача представляет собой вопрос, на который надо найти ответ, опираясь на те условия, которые указаны в задаче. Поэтому, приступая к решению задачи, ее надо внимательно изучить, установить, в чем состоят ее вопросы, каковы условия, исходя из которых надо решать задачу. Результаты такого предварительного анализа надо как-то зафиксировать. Схематичная запись задачи должна быть удобна и наглядна.
Чтобы каждому ученику обеспечить возможность решать задачу с необходимыми объяснениями и в определенной последовательности, ему дается список указаний.
- О каком процессе идет речь в задаче?
- Какие величины характеризуют этот процесс?
- Каким соотношением связаны эти величины?
- Сколько различных процессов описывается в задаче?
- Есть ли связь между элементами?
Отвечая на эти вопросы (эти указания у каждого ученика есть на обложке тетради), ученики анализируют условие задачи, записывают его схематично. Эта схема – сетевой граф. Таким способом можно решать текстовую задачу, величины которой связаны соотношением A=BxC.
Задача 1.
Расстояние между деревнями Емелино и Петровка равно 30 км. Изобразите дорогу между этими деревнями в виде школы, деления которой обозначают 3 км. Покажите на этой школе, где окажется через 1 час, через 2 часа пешеход, идущий из Емелино в Петровку со скоростью 6 км/ч. Покажите, где он окажется через 3 часа после выхода, через 4 часа, через 5 часов?
При ответе на поставленные вопросы получается удобным повторение следующих моментов:
Расстояние между двумя пунктами удобнее всего изображать в виде отрезка, само же расстояние, как число, есть длина этого отрезка;
Что такое скорость?
Скорость движения – это расстояние, которое проходит человек за единицу времени (1 ч, 1 мин. и т. п.). Есть общепринятое обозначение терминов – расстояние (пройденный путь), скорость движения, время: S, v, t.
Нарисовали шкалу, обозначили начало отсчета E и С – точку, соответствующую числу 30, разбили отрезок EC делениями (штрихами) ценой 3 км. Говоря о движении, мы имеем в виду, что три величины характеризуют этот процесс: путь S, скорость v, время t.
Где был пешеход через 1 час после выхода? Это расстояние, которое прошел пешеход за 1 час, или скорость движения пешехода. Последний вопрос: где оказался пешеход через 5 ч?
Вывод: чтобы найти путь S, надо скорость движения умножить на время нахождения в пути. Записываем формулу S=vxt, повторяем, как найти v, зная расстояние и время движения, как найти время, зная расстояние и скорость движения. Теперь можно приступать к решению текстовых задач.
Задача 2.
Автобус шел 2 часа со скоростью 45 км/ч. Потом он шел 3 часа со скоростью 60 км/ч. Какой путь прошел автобус за эти 5 часов?
Все записи на сетевом графе делаем простым карандашом от руки. Сетевой граф вычерчивается на доске и в тетради.
Действия учителя и учеников.
1. О каком процессе идет речь?
- О движении.
2. Какие величины характеризуют этот процесс?
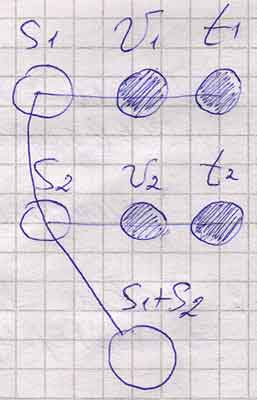
- Путь, скорость, время (на доске и в тетради рисуются три кружка, подписываются буквы).
3. Каким соотношением связаны величины?
- S=vxt
4. Сколько различных процессов описывается в задаче?
- Два: одно движение со скоростью 45 км/ч, второе – 60 км/ч (у букв S, v, t ставим внизу 1 и рисуем еще три кружка, соединяя их линией, обозначаем их S2,v2,t2).
5.Есть ли связь между одноименными элементами? (элементами являются S1 и S2, v1 и v2, t1 и t2. Отыскиваем связь, читая условие; заштриховываем сплошным кружок величины, которая известна, и подписываем).
- Два часа со скоростью 45 км/ч.
- Три часа со скоростью 60 км/ч.
- Какое расстояние прошел автобус за 5 ч? (Надо найти весь путь, который прошел автобус, поэтому через S1 и S2 проводим линию и завершаем ее кружком S1+S2).
На доске и в тетради получается граф к задаче. Чтобы решить задачу, надо заштриховать все кружки. Каждая линия, а их три, называется ребром. Принцип штриховки: имея два заштрихованных кружка на одном ребре, найти (заштриховать) третий. Те кружки, которые заполняем, решая задачу, штрихуются редкой полоской (от руки).
Поясним: первое ребро v1=45 км/ч, t1=2ч. Можно найти S1? S1=45x2=90(км), можно заштриховать кружок S1, перечеркиваем использованное ребро. Аналогично, второе ребро, величина S2. Остается третье, в котором уже заштрихованы два кружка S1и S2. Рассуждая, параллельно ведется запись решения задачи с обязательным пояснением к каждому действию.
Итак.
45х2=90(км) – прошел автобус за 2 ч
60х3=180(км) – прошел автобус за 3 ч
90+180=270 (км) – прошел автобус за 5 ч.
Ответ: 270 км.
Задача на дом.
Лыжник за 5 часов прошел 75 км. Сколько времени ему потребуется, чтобы с той же скоростью пройти 60 км?