Фибоначчиева система счисления

Фибоначчиева система счисления — смешанная система счисления для целых чисел на основе чисел Фибоначчи F2=1, F3=2, F4=3, F5=5, F6=8 и т.д. Последовательность Фибоначчи определяется следующим образом: F0 = 0 F1 = 1, Fn = Fn-1 + Fn-2. Несколько первых её членов : 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...

История

Эти числа ввёл в 1202 г. Леонардо Фибоначчи (Leonardo Fibonacci) (также известный как Леонардо Пизанский (Leonardo Pisano)). Однако именно благодаря математику 19 века Люка (Lucas) название "числа Фибоначчи" стало общеупотребительным. Впрочем, индийские математики упоминали числа этой последовательности ещё раньше: Гопала (Gopala) до 1135 г., Хемачандра (Hemachandra) — в 1150 г.

Свойства

Числа Фибоначчи обладают множеством интересных математических свойств.

Вот лишь некоторые из них:

   * Соотношение Кассини: 
     

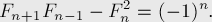
   * Правило "сложения": 
     

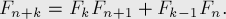
   * Из предыдущего равенства при k = n вытекает: 
     

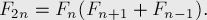
   * НОД-равенство: 
     

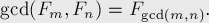
Фибоначчиева система счисления

Теорема Цекендорфа утверждает, что любое натуральное число n можно представить единственным образом в виде суммы чисел Фибоначчи:

где k1 \ge k_2+2, k_2 \ge k_3+2, \ldots, k_r \ge 2 (т.е. в записи нельзя использовать два соседних числа Фибоначчи).

Отсюда следует, что любое число можно однозначно записать в фибоначчиевой системе счисления, например: