Копилка знаменитых задач продолжение 6

Материал из ТолВИКИ

Версия от 15:16, 13 ноября 2008; Bookworm ID 213 (обсуждение | вклад)

(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)

Перейти к: навигация, поиск

Посмотреть страницу Копилка знаменитых задач.

Содержание

1 Задачи участников ДООМ
2 МаГмА ID _205
3 Совокупность "жареных семечек"ID-224
4 Участник: Максимум ID_251
5 Совокупность "жареных семечек"

Задачи участников ДООМ

--Bookworm ID 213 13:03, 4 ноября 2008 (UZT)

Задача № 39. Старинная задача: Один пастух говорит другому: «Дай мне одну из твоих овец и у меня буде вдвое более овец чем у тебя». Второй пастух отвечает: Нет, лучше ты дай мне одну из твоих овец, тогда у нас будет овец поровну». Сколько овец было у каждого пастуха? Решение: Обозначим кол-во овец первого пастуха за х, а кол-во овец у второго – у. Тогда получим систему из двух уравнений: х+1=(у-1)2 и х-1=у+1. Решая систему получим, что х=7, а у=5. Ответ: у первого пастуха было 7 овец, а у второго 5.

Задача № 40. Задача Льюиса Кэррола. Несколько человек сидят по кругу так, что у каждого из них имеется по одному соседу справа и слева. Каждый из сидящих располагает определенным количеством шиллингов. У первого на 1 шиллинг больше, чем у второго, у второго на 1 шиллинг больше, чем у третьего, и т. д. Первый из сидящих отдает 1 шиллинг второму, второй 2 шиллинга третьему и т. д. Каждый отдает следующему на 1 шиллинг больше, чем получил сам, до тех пор, пока, это возможно. В результате у одного из сидящих шиллингов оказывается в 4раза больше, чем у его соседа. Сколько всего было людей и сколько шиллингов было сначала у самого бедного из них? Решение: Пусть m–число людей, k–число шиллингов у последнего (самого бедного) из них. После первого тура каждый из участников игры станет на 1 шиллинг беднее, а сумма, передаваемая последним из игроков первому, составит m шиллингов. Следовательно, после некоторого числа k туров каждый участник станет беднее на k шиллингов, у последнего участника не останется ни одного шиллинга, а сумма передаваемая им первому участнику, составит mk шиллингов. Игра прекратится на следующем туре, когда очередь пополнять «передвижную кассу» дойдет до последнего игрока. В это момент в «кассе» будет mk+m–1 шиллингов, у предпоследнего игрока не останется ничего, а у первого m–2 шиллингов. Ясно, что единственными участниками, «состояния» которых относятся как 4:1, могут быть лишь первый и последний игроки. Следовательно, mk+m–1=4(m–2), либо 4(mk+m–1)=m–2. Первое уравнение преобразуем к виду mk=3m–7, или k=3–7/m. Ясно, что оно не имеет иных решений в целых числах, кроме m=7, k=2. Второе уравнение преобразуется к виду 4mk=2–3m. Оно не имеет решений в целых положительных числах. Ответ: 7 человек, 2 шиллинга.

Задача №41. Задача Льюиса Кэррола. 1 июля, когда на моих карманных часах было 8 часов утра, стенные часы показывали 8часов 4 минуты. Взяв с собой карманные часы, я отправился в Гринвич и обнаружил, что, когда они показывают полдень, точное время в действительности равно 12часам 5 минутам. Вечером того же дня, когда на моих часах было ровно 6 часов, стенные часы показывали 5часов 59 минут. 30 июля в 9 часов утра по моим карманным часам стенные часы показывали 8часов 59 минут. В Гринвиче, когда мои карманные часы показывали 12 часов 10 минут, точное время было 12часов 5 минут. Вечером того же дня карманные часы уже показывали 7 часов, когда на стенных ещё было 6 часов 58 минут. Карманные часы я завожу лишь при поездке в Гринвич. В течении суток они идут равномерно. Настенные часы идут всегда, причем идут равномерно. Каким образом мне узнать, когда наступает полдень (по точному времени) 31 июля? Решение: 1 июля мои карманные часы за 10 ч ушли вперед по сравнению со стенными часами на 5 мин, то есть спешили на ½ мин в час, или на 2 мин в 4 часа. Следовательно, когда карманные часы показывали полдень, на стенных часах было 12ч 2 мин. Иначе говоря, в тот момент, когда точное время было 12ч 5мин, стенные часы отставали на 3мин (от точного времени). 30 июля карманные часы отстали от стенных на 1мин за 10ч, то есть отставали на 6с в час, или на 19с за 3ч 10мин. Таким образом, когда карманные часы показывали 12ч 10мин, на стенных было 12ч 7мин 19с. иначе говоря, в момент, когда точное время было 12ч 5мин, стенные часы спешили на 2мин 19с (по сравнению с точным временем). Итак, стенные часы уходят вперед по сравнению с точным временем на 5мин 19с за 29дней, что составляет 319с за 29дней, или 11с в день, или 11/24*12с за 5мин. Следовательно, 5 мин точного времени соответствует 5мин 11/288с, отсчитанным по карманным часам. 31 июля, когда точное время равнялось 12ч 5мин, стенные часы ушли вперед на 2мин 19с+11с, то есть показывали 12ч 7½мин. Следовательно, если вернуться на 5мин назад по точному времени, то стрелки стенных часов следует отвести на 5мин 11/288с назад, то есть поставить так, чтобы они показывали12ч 2мин 29 277/288с. Ответ: в момент, когда 31 июля стенные часы показывают это время, по точному времени наступает полдень.

Задача №42. Задача Льюиса Кэррола. Два пешехода А и В пускаются в путь ровно в 6 часов утра в один и тот же день. Оба идут по одной дороге и в одном направлении. Пешеход В сначала опережает пешехода А на 14 миль. Оба идут с 6 утра до 6 вечера. В первый день пешеход А, двигаясь с постоянной в течении дня скоростью, проходит 10 миль, во второй - 9, в третий – 8 миль и т. д. Пешеход В, двигаясь также с постоянной в течении дня скоростью, проходит в первый день 2 мили, во второй – 4, в третий 6 и т. д. Где и когда пешеход А нагонит Пешехода В? Решение: Пусть х - число дней, прошедших с того момента, как пешеходы пустились в путь, до встречи. Тогда: [2*10–([х–1)]*х/2=14+[2*2+( х–1)*2]*х/2 То есть: 21х/2 – х2/х=14+х+х2 3х2–19х+28=0 х1=4, х2=7/3. Ответ 7/3 указывает на то, что встреча происходит на 3-й день. Ведем у – число часов, которое пешеходы находятся в пути. Отсчитывается с 6-ти часов утра каждого дня. К концу второго дня пути А пройдет 19 миль, а В будет находиться от пункта отправления А на расстоянии 14+6=20 миль. Следовательно, 19 + у*8/12=20+у*6/12 у*2/3=1+у*1/2 откуда у= 6. Таким образом, пешеходы встречаются по происшествии двух с половиной дней (2 дня 6 ч) и четырех дней пути на расстояниях в 23 и 34 мили от отправного пункта пешехода А.

Задача №43. Задача Льюиса Кэррола. Пятеро друзей решили на паях организовать компанию по торговле вином. Каждый из них внес в фонд компании одинаковое количество бутылок, купленного по одной цене. Один из друзей на общем собрании «акционеров» был избран казначеем, другой - продавцом. В обязанность продавцу вменялось продавать вино с 10%-ной надбавкой (по сравнению с покупной ценой). В первый день продавец распил одну бутылку вина, несколько бутылок продал, а всю выручку передал казначею. На второй день продавец не стал пить вина, но прикарманил деньги, полученные от продажи одной бутылки, а всю остальную выручку передал казначею. Вечером того же дня казначей наведался в погреба фирмы и пересчитал оставшиеся бутылки. «вина ровно на 11 фунтов стерлингов», - заметил он себе под нос, покидая погреб. На третий день продавец выпил одну бутылку вина, присвоил себе деньги, полученные от продажи другой бутылки, а всю остальную выручку передал казначею. Поскольку все вино было продано, друзья созвали общее собрание «акционеров» и к своему огорчению обнаружили, что их доходы (то есть разность между суммами, переданными продавцом казначею , и первоначальной стоимостью вина) составили лишь 6 пенсов за бутылку. Доходы эти поступали в течении трех дней равномерно (то есть разность между выручкой, переданной продавцом казначею в конце каждого дня, и первоначальной стоимостью проданного за день вина была одной и той же в течение всех трех дней), но об этом, разумеется, знал лишь продавец. 1. Сколько бутылок вина было куплено в фонд компании? 2. По какой цене друзья покупали вино? Решение: Обозначим число бутылок вина, проданных в первый, второй и третий день, через х, у, z. Предположим, что каждая бутылка была куплена за 10v пенсов и, следовательно, продана за 11v пенсов. В первый день казначей получил от продавца (х–1 )*11v, во второй у*11v –v и в третий день (z –1) *11v–v пенсов. Следовательно, прибыль (разность между выручкой и затратами на покупку вина) составила: в первый день хv–11 , во второй день уv–v и в третий zv-12v пенсов. По условию задачи все три величины равны, откуда у=х–10, z=х+1. Таким образом, полное число бутылок (х+у+z), хранившихся в начале в винном погребе «фирмы», равно 3х – 9. Прибыль от продажи всех бутылок составила (х+у+z)v–24v=(3х–33)v, а прибыль от продажи одной бутылки равна [(3х–33)v]/3х–9.(По условию задачи эта величина равна 6 пенсам.) (х–11)v=(х–3)6 Кроме того, z*11v=11*240, то есть (х+1)*11v=11*240. Комбинируя эти два уравнения, получаем: (х–11)/х+1=6(х–3)/240 (х+1)(х–3)=40(х–11) х2–2х–3=40х–440 х2–42х+437=0 х1,2=(42±4)/2, х1=23, х2=19. Итак, число бутылок равно либо60, либо 48, но поскольку оно должно быть кратно 5, остается лишь одно решение: 60 бутылок. Поскольку(х+1)*11v=11*240, или 24v= 240, то v=10. таким образом, вино было куплено по цене 8 шиллингов 4 пенса за бутылку и продано по цене 9 шиллингов 2 пенса за бутылку. Ответ: Было куплено 60 бутылок, по цене 8 шиллингов 4 пенса за бутылку. --Bookworm ID 213 13:03, 4 ноября 2008 (UZT)

Задачи команды ЛАДА-ВЕКТОР ID_279

Задача №15

Задача из папируса Ахмеса, Египет, ок. 2000г. до н.э.

Приходит пастух с 70 быками. Его спрашивают : «Сколько приводишь ты из своего многочисленного стада?» Пастух отвечает «Я привожу две трети от трети скота. Сочти. Сколько быков в стаде?

Решение: 70быков – 2/3 от трети скота

70:2/3=105(быков) – треть скота

105:1/3=315(быков)

Ответ: В стаде 315 быков.

Задача №16

Задача Евклида, Греция

Ослица и мул шли вместе, нагруженные мешками равного веса. Ослица жаловалась на тяжесть ноши.«Чего ты жалуешься? -сказал мул. Если ты дашь мне один свой мешок моя ноша станет вдвое больше твоей, а если я дам тебе один мешок наши грузы сравняются». Сколько мешков было у каждого?

Решение:

Обозначим за Х число мешков у каждого после передачи одного мешка от мула к ослице. Тогда первоначально у мула было (Х+1) мешков , а у ослицы (Х-2) в два раза меньше, чем у мула.

Составим и решим уравнение:

х+2=2(х-2)

х+2=2х-4

х=6

6+1=7(мешков)- у мула

6-1=5(мешков)- у ослицы

Ответ: 5мешков у ослицы и 7мешков у мула.

Задача №17

Старинная задача

На вопрос о возрасте одна дама ответила: «Мой возраст таков ,что если его возвести в квадрат или умножить на 53 и из результата вычесть 696 ,то получится одно и тоже».

Решая квадратное уравнение, автор замечает: «Так как вопрос касается возраста дамы, то из вежливости нужно перед радикалом поставить нижний знак».

Решим эту задачу с этим дополнительным условием.

Пусть даме x лет. Составим уравнение:

x = 53x – 696,и решим его беря (из вежливости) перед радикалом нижний знак.

x – 53x + 696 = 0

Д = 53 – 4 × 696 = 2809 - 2784 =25, квдратный корень из 25 = 5.

Получим x = (53- 5)/2=24. Итак, даме было 24 года.

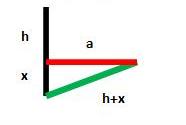
Задача № 18

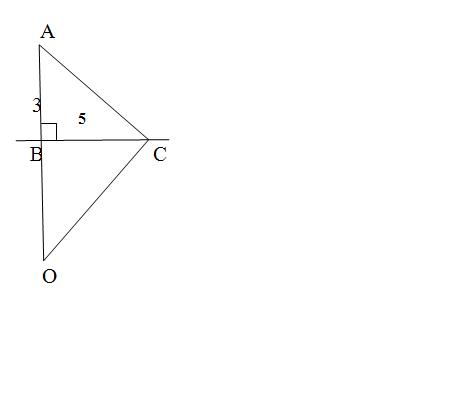
Задача Ал – Каши

Копьё стояло в воде отвесно и высовывалось наружу на 3 локтя. Порыв ветра наклонил его , причём нижний конец копья не изменил положение ,а верхний оказался на поверхности воды на расстоянии 5 локтей от того места где раньше копьё высовывалось из воды. Мы хотим узнать длину копья.

Решение:

Сделаем рисунок.

Введём обозначения.

АО перпендикулярно ВС,

АВ = 3 локтя,ВС = 5локтей

Найдём АО.

АО = АВ + ВО

Найдём ВО.

Рассмотрим прямоугольные подобные треугольники АВС и ВСО.

Из подобия треугольника АВС и треугольники ВСО:

АВ/ВС= ВО

3/5=5/ВО

Во = 25/3=8 1/3

АО=АВ=ВО=3+8 1/3=11 1/3 (локтя)

Ответ: Длина копья 11 1/3 локтя.

Задача №19

Задача древнего Китая

Город имеет форму квадрата, в середине каждой стороны которого имеются ворота. Вне города, на расстоянии 20 бу север от северных ворот, стоит столб. Если пройти от южных ворот 14 бу на юг, а затем повернуть на запад и пройти ещё 1775 бу, то как раз в этот момент из-за стен города покажется столб. Какова ширина города?

Задача № 20

Задача (Из арифметики Л.Ф. Магницкого.)

У некоторого человека были для продажи вина двух сортов. Первое ценною 10 гривен ведро, второе же – по 6 гривен. Захотелось ему сделать из тех двух вин, взяв по части, третье вино, чтобы ему цена была по 7 гривен. Какие части надлежат из тех двух вин взять к наполнению ведра третьего вина ценою 6 гривен.

Современное решение:

Пусть для составления одного ведра требуемой смеси нужно взять х ведер первого сорта (х 1) и (1-х) ведер второго сорта. первая часть вина стоит 10х гривен, а вторая 6(1-х) гривен.

Составим уравнение:

10х+6(1-х) = 7, откуда х =1/4 , 1 – х = 3/4 .

Итак, нужно взять 1/4 ведра вина по 10 гривен и 3/4 ведра вина по 6 гривен за ведро.

Старинный способ решения:

Запишем цены вин каждого сорта и цену смеси так:

Вычислить прибыль 7-6=1 и убыток 10-7=3 на каждом ведре и запишем результат по линиям:

Таким образом, 3 части из четырёх приходятся на более дешевое вино и 1 часть – на более дорогое.

--Лада-Вектор ID 279 22:30, 4 ноября 2008 (UZT)

Задача № 21

Задачи из «Арифметики» Л.Ф.Магницкого.

Собака и заяц. Собака усмотрела зайца в 150 саженей от себя. Заяц пробегает за 2 минуты 500 саженей, а собака- за 5 минут 1300 саженей. За какое время собака догонит зайца? Решение: За одну минуту заяц пробегает 250 саженей, а собака 260 саженей. Следовательно, за одну минуту расстояние между собакой и зайцем уменьшиться на 10 саженей. Поскольку между собакой и зайцем, когда собака увидала зайца, было 150 саженей, то собака догонит зайца через 150 х 10= 15 минут.

Задача №22

Задачи из «Арифметики» Л.Ф.Магницкого.

Два воина.

Один воин вышел из города и проходил по 12 верст в день, а другой вышел одновременно и шел так: в первый день прошел 1 версту, во второй день 2 версты, в третий день 3 версты, в четвертый день 4 версты, в пятый 5 верст и так прибавлял каждый день по одной версте, пока не настиг первого. Через сколько дней в второй воин настигнет первого? Решение: В первый день второй воин отстанет на 12 – 2 = 11 верст, во второй еще на 12 – 2 = 10 верст, в третий еще на 12- 3 =9 верст и так далее. На 12 ый день отставание составит (11 +10+9+…+2+1+0) верст. А затем расстояние между ними начнет сокращаться. В 13- й день на 13 – 12 = 1 версту, в 14 день еще на 14 – 12 = 2 версты, в 15 –й день еще на 15 – 12 =3 версты, и , наконец , в 23-й день на 23 – 12= 11 верст. На 23-й день расстояние между ними уменьшиться на ( 1+2+3+…+10+11) верст. Это значит, что второй воин по прошествии 23 дней догонит первого.

Задача №23

Задача XVIII века.

«С чем иностранка к россам привезена?»

Нововыезжей в Россию иностанной мадаме

Вздумалось оценить свое богатство в чемодане:

Новой выдумки нарядное фуро

И праздничный чепец а ля фигаро.

Оценщик был русак,

Сказал мадаме так:

«Богатство твоего первая вещь фуро

Вполчетверта дороже чепца фигаро;

Вообще же не с половиной четыре алтына,

Но настоящая им цена только сего половина»

Спрашивается каждой вещи цена,

С чем иностранка к россам привезена?

(« Вполчетверта»- в 3 1/2 раза).

Решение:

Все имущество мадам было оценено в 1/2 х (4 +1/2) алтынов, что составляет 27/4 копеек. « Чепец фигаро» по условию в 3 1/2 раза дешевле «фуро», и, следовательно , в 4 1/2=9/2 раза дешевле всего имущества. Поэтому чепец стоит 27/4 : 9/2 = 3/2 копейки, а стоимость «фуро» равна 3/2х 31/2=21/4 копейки

Задача №24

Задача XVIII века.

Три бочки.

Хозяин имеет три бочки А,В и С. Бочка А наполнена квасом, бочки В и С- пустые. Если квасом из бочки А наполнить бочку В, то в бочке А останется 2/5 ее содержимого .Если же квасом из бочки А наполнить бочку С, то в бочке А останется 5/9 ее содержимого. Чтобы наполнить обе бочки В и С, надо взять содержимое бочки А и еще добавить 4 ведра кваса. Сколько ведер кваса вмещает каждая бочка?

Решение

Так как после наполнения бочки В в бочке А остается 2/5 ее содержимого, то вместимость бочки В равна3/5 вместимости А. Так как после наполнения бочки С в бочке А остается 5/9ее содержимого, то вместимость бочки С равна 4/9 вместимости бочки А.Значит , вместимость бочек. В и С равна – 3/5+4/9= 47/45=1+ 2/45 вместимости бочки А. Из условия задачи тогда следует, что 2/45 Вместимости бочки А составляют 4 ведра , откуда получаем , что вместимость бочки В равна 90 х 4/9= 40 ведер.

--Лада-Вектор ID 279 23:30, 5 ноября 2008 (UZT)

--Bookworm ID 213 14:15, 5 ноября 2008 (UZT) Задача № 44:Задача из акмимского папируса. Некто взял из сокровищницы 1/13. Из того, что осталось, другой взял 1/17, оставив же он в сокровищнице 150. Сколько было в сокровищнице первоначально? Решение: В рукописи дробная часть ответа 17221/32 дается в виде суммы дробей, числители которых равны 1, а именно: 1/2 + 1/8 + 1/48 + 1/96. Ответ: В сокровищнице было 17221/32.

Задача № 45:Задача Диофанта (из трактата «Арифметика»). Требуется число 100 разделить два раза так, чтобы большая его часть от первого деления была вдвое более меньшей части от второго деления и чтобы большая часть от второго деления Решение: Обозначим меньшую часть от второго деления через х, тогда большая часть от первого деления будет 2х. Найдем теперь меньшую часть от первого деления. Она будет равна 100 – 2х. Следовательно, большая часть второго деления равняется 300 – 6х. Ясно, что обе части от второго деления должны составить 100, т. е. х+(300 – 6х) = 100, откуда х = 40. Следовательно, результат первого деления: меньшая часть равна 20, большая – 80. Результат второго деления: меньшая часть равна 40, большая часть – 60. Ответ: Результат первого деления: меньшая часть равна 20, большая – 80; результат второго деления: меньшая часть равна 40, большая часть – 60.

Задача № 46: Задача из греческой антологии. Видя, что плачет Эрот, Киприда его вопрошает: «Что так тебя горчило, ответствуй немедля!» «Яблок я нес с Геликона немало, - Эрот отвечает, - Музы, отколь ни возьмись, напали на сладкую ношу Частью двенадцатой вмиг овладела Евтерпа, а Клио Пятою долю взяла. Талия – долю восьмую. С частью двадцатой ушла Мельпомена. Четверть взяла Терпсихора, С частью седьмой Эрато от меня убежала. Тридцать плодов утащила Полимния. Сотня и двадцать Взяты Уранией; триста плодов унесла Каллиопа. Я возвращаюсь домой почти что с пустыми руками, Только полсотни плодов мне оставили музы на долю». Решение: Пусть «Яблоки Эрота» - х, тогда осталось у него х – (1/12 х + 1/5 х + 1/8 х + 1/20 х + 1/4 х + 1/7 х) = 30 + 120 + 50. Решая уравнение получаем 25/168 х = 200, из этого х = 1344 яблока. Ответ: У Эрота было 1344 яблока.

Задача №47: Задача из греческой антологии. Вот Полифема циклопа из меди статуя отлита. Руку, уста и единое око ваятель сделал на диво, Скрывши в них трубы: водой великан истекает как будто. Хитрое в трубах устройство: ведущая в руку способна Весь водоем до краёв через три дня наполнить. Оку – достаточно дня, а устам и всего лишь две пятых, Вместе все три водоём скоро ли могут наполнить? Решение: Пусть водоем – 1, тогда скорости: руки – 3, ока – 1, уст – 2/5 . Получаем уравнение: 1: (3 + 1 + 2/5) = 4 2/5 дня. Ответ: За 4 2/5 дня рука, око и уста заполнят водоем.

Задача №48: Задача из греческой антологии.- Хроноса (бог времени) вестник, скажи, какая часть дня миновала? - Дважды две трети того, что прошло, остаётся. (У древних греков день длился 12 часов.) Решение: Задача сводится к решению уравнения 4/3 х + х = 12, откуда х = 5 1/7 дня. Ответ: 5 1/7 дня миновала. --Bookworm ID 213 14:15, 5 ноября 2008 (UZT)

Участник:ПОБЕДА ID_235

1. Четверо братьев

ЗАДАЧА

У четырех братьев 45 рублей. Если деньги первого увеличить на 2 рубля, деньги второго уменьшить на 2 рубля, деньги третьего увеличить вдвое, а деньги четвертого уменьшить вдвое, то у всех окажется поровну. Сколько было у каждого?

РЕШЕНИЕ

Пусть x руб. - у первого брата, y руб. - у второго брата, z руб. - у третьего брата, t руб. - у четвертого брата.

Составим уравнение:

x + 2 = y - 2 = 2z = t/2

Расчленяем уравнение на три отделоных и решаем.

x + 2 = y - 2

x + 2 = 2z

x + 2 = t/2. Получаем следующие ответы: x = 8, y = 12, z = 5, t = 20.

У первого брата 8 руб., у второго - 12 руб., у третьего - 5 руб., у четвертого - 20 руб.

2. Задача Д.И.Менделеева

Великий русский ученый Д.И.Менделеев, будучи директором Главной палаты мер и весов, интересовался задачей на взвешивание при помощи одного набора гирь. Задача заключаласб в следующем: "Если иметь набор гирь по одной каждого вида, например a, b, c, d г., то по скольку граммов должны быть эти гири, чтобы при помощи их можно было взвесить любой груз, не превышающий a + b + c + d граммов.

ЗАДАЧА

Пусть имеется любой груз в 86 г. Какие нужно выбрать гири, чтобы, имея только один набор их, уравновесить это груз, если положить гири только на правую чашку весов?

РЕШЕНИЕ

Так как всякое натуральное число можно выразить в двоичной чистеме счисления, где в каждом разряде может быть не более одной единицы, то получается, что всякое натуральное число может быть представлено в виде суммы степеней 2 и 1. На этом свойстве и основывается возможность на весах всякий груз, содержащий целое число граммов, гирями "двоичной системы счисления". Число 86 в двоичной будет 1010110 = 2⁶ + 2⁴ + 2² + 2 = 64 + 16 + 4 + 2. Имея набор гирь, груз 86 г может быть уравновешен гирями 64 г, 16 г, 4 г, 2 г.

3. Вечеринка

ЗАДАЧА

На вечеринке было 20 танцующих. Мария танцевала с семью танцорами, Ольга - с восемью, Вера - с девятью и так далее до Нины,Ю которая танцевала со всеми танцорами. Сколько танцоров (мужчин) было на вечеринке?

РЕШЕНИЕ

Будем искать число не танцоров, о танцорок, которое обозначим за x:

1-я, Мария, танцевала с 6 + 1 танцорами

2-я, Ольга,танцевала с 6 + 2 танцорами

3-я, Вера, танцевала с 6 + 3 танцорами

........................................

x-я, Нина, танцевала с 6 + x танцорами

Имеем уравнение

x + (6 + x) = 20

Откуда

x = 7,

Найдем количество танцоров:

20 - 7 = 13

7 танцоров было на вечеринке.

4. Мнимая нелепость

ЗАДАЧА

Чему равно 84, если 8*8=54?

РЕШЕНИЕ

Пусть основание неизвестной чистемы счисления - x. Число "84" означает тогда 8 единиц второго разряда и 4 единицы первого, т.е. "84" = 8x + 4.

Число "54" означает 5x + 4. Имеем уравнение 8*8=5x + 4, т.е. в десятичной системе 64 = 5x + 4, откуда x = 12. Числа написаны по двенадцатеричной системе, и "84" = 8*12 + 4 = 100. Значаит, если 8*8="54", то "84" =100.ъ

5. Утопить или повесть

ЗАДАЧА

Некто совершил преступление, караемая смертной казнью. На суде ему предоставляется последнее слово. Он должен произнести одно утверждение. Если оно окажется истинным - преступника утопят, если же оно окажется ложным, то преступника повесят. Какое утверждение он должен высказать, чтобы привести палачей в полное замешательство?

ОТВЕТ: Я буду повешен.

6. Парадокс цирюльника

ЗАДАЧА

В небольшом городке цирюльник бреет всех, кто не бреется сам и не бреет никого из тех, кто бреется сам. Бреет ли цирюльник самого себя? Если он бреет самого себя, то тем самым он нарушает правила, так как бреет одного из тех, кто бреется сам. Если же цирюльник не бреет самого себя, то он опять-таки нарушает правила, так как не бреет одного из тех, кто не бреется сам. Что делать цирюльнику?

ОТВЕТ: существование такого цирюльника логически невозможно.

7. Математический ребус

ЗАДАЧА

ЧАЙ : АЙ = 5.

РЕШЕНИЕ

Из условия следует, что ЧАЙ = АЙ * 5, т.е. Ч*100+АЙ=АЙ*5, откуда Ч*100=АЙ*4 и Ч*25=АЙ. Так как число АЙ двузначное, то Ч может быть равно только 1,2 или3. Каждому значению Ч соответствует определенное решение: если Ч=1, то АЙ=25, разные буквы расшифровываются разными цифрами., А=2, Й=4, если Ч=2, то АЙ =50; если Ч=3, то АЙ=75. Значит, расшифровать запись можно тремя способами: ЧАЙ=125, 250 или 375.

--Bookworm ID 213 15:30, 6 ноября 2008 (UZT) Задача 49. Магницкого Л.Ф. Путешественники.Путешественник идет из одного города в другой 10 дней, а второй путешественник тот же путь проходит за 15 дней. Через сколько дней путешественники встретятся, если выйдут одновременно навстречу друг другу из этих городов? Решение. За тридцать дней путешественники проходят 30: 10 + 30: 15 = 5 расстояний между городами. Значит, они сойдутся через 30:5 = 6 дней.

Задача 50. Магницкого Л.Ф. Вокруг города. Два человека пошли одновременно друг за другом из одного места вокруг города. Один из них идет по 4 версты в час, а второй по 3 целых 1/3 версты в час. Путь вокруг того же города составляет 15 верст. Через сколько часов они сошлись и сколько раз каждый из них обошел город? Решение. За первый час второй путник отстанет от первого на 4 – 10/3 = 2/3 версты. За второй час еще на 2/3 версты, за третий час еще на 2/3 версты и т.д. Путники сойдутся вместе опять, когда отставание сравняется с длиной пути вокруг города , то есть станет равным 15 верстам. На это понадобится 15: 2/3 = 22 ½ час. Первый путник за это же время пройдет 4 * 22 ½ = 90 верст и обойдет 90: 15=6 раз вокруг города. Второй путник пройдет на 15 верст меньше и сделает на один обход меньше. Таким образом, путники сойдутся опять через 22 ½ часа. Первый из них обойдет вокруг города 6 раз, второй 5 раз.

Задача 51. Магницкого Л.Ф. Деревня. Прохожий, догнавший другого, спросил: «Как далеко до деревни, которая у нас впереди?». Отвечал другой прохожий: « Расстояние от той деревни, от которой ты идешь, равно третьей части всего расстояния между деревнями, а если еще пройдешь 2 версты, тогда будешь ровно посередине между деревнями». Сколько верст осталось еще идти первому прохожему? Решение. До середины расстояния между деревнями первому прохожему нужно идти 2 версты, и это составляет 1/2 - 1/3 = 1/6 часть всего расстояния между деревнями. Поэтому расстояние между деревнями равно 12 верстам, к моменту встречи первый прохожий прошел 1/3 · 12 =4 версты и осталось ему идти еще 8 верст.

Задача 52. Магницкого Л.Ф. Один путник идет от города до дома 17 дней, другой то же расстояние от дома до города за 20 дней. Оба вышли в один и тот же час и из своих мест. Через сколько дней они встретятся? Решение. Обозначим весь путь за 1, тогда 1:( 1/17 + 1/20 ) = 1 : 37/340 = 340 / 37 = 9 + 7 / 37 Ответ: 9 +7/37 дней --Bookworm ID 213 15:30, 6 ноября 2008 (UZT)

Шоу "модель" ID_278

Задача из Вьетнама.Для кормления 100 буйволов заготовили 100 охапок сена. Стоящий молодой буйвол съедает 5 охапок сена. Лежащий молодой буйвол - 3 охапки сена. Старые буйволы втроём съедают 1 охапку сена. Сколько молодых буйволов стоят, сколько лежат и сколько буйволов старых?

Решение: Пусть x - число стоящих, y - число лежащих молодых буйволов и z - число старых буйволов. Тогда x+y+z=100, 5x+3y+z/3=100,y=25-7x/4. Так как x и y натуральные числа, то последнее равенство выполняется только при x=4,8,12. Задача допускает следующие решения x=4,y=18,z=78; 8, y=11, z=81; x=12, y=4, z=84.

Задача Шен Кана. Три снопа хорошего урожая, 2 снопа среднего урожая и 1 сноп плохого дают 39 доу (китайская мера) зерна. Два снопа хорошего урожая, 3 снопа среднего и 1 сноп плохого дают 34 доу. Один сноп хорошего, 2 снопа среднего и 3 снопа плохого урожая дают 36 доу зерна. Сколько доу зерна даёт 1 сноп хорошего, 1 сноп среднего и 1 сноп плохого урожая?

Решение:Пусть сноп хорошего урожая даёт x - доу зерна, среднего - y доу, плохого - z доу. Тогда 3x+2y+z=36, 2x+3y+z=34, x+2y+3z=36, откуда x=9,25 y=4,25 z=2,75.

Задача греческого математика Митродора.Царская корона имеет массу 60 мин (1 мина=100 драхм=1/60 таланта) и отлита из сплава золота, меди, свинца и железа. На золото и медь приходится 3/4, на золото и свинец - 2/3, на золото и железо - 3/5 массы короны. Сколько мин золота, меди, свинца и железа в царской короне?

Решение:Предположим, что на отливку короны пошло x мин золота, y мин меди, z мин свинца и f мин железа. Тогда x+y+z+f=60,(1). x+y=2/3*60=40,(2). x+z=3/4*60=45,(3). x+f=3/5*60=36,(4). Складывая уравнения (2),(3),(4), получаем 3x+y+z+f=121, вычитая из последнего уравнения уравнение (1), находим 2x=61,x=30,5. Значит y=9,5 z=14,5 f=5,5.Итак, 30,5 мин золота, 9,5 мин меди, 14,5 мин свинца и 5,5 мин железа.

Участник:Шоу "модель" ID_278--Шоу "модель" 16:44, 6 ноября 2008 (UZT)

--Bookworm ID 213 16:53, 7 ноября 2008 (UZT)

Задача №53. Задача французского автора Ж. Озанама (XVII в.)

Трое хотят купить дом за 24000 ливров. они условились, что первый даст половину, второй одну треть, а третий оставшуюся часть. Сколько денег даст каждый?

Решение:

1) Найдем, сколько денег даст первый человек: 24000*0,5=12000 (ливров) 2) Найдем количество денег, которое даст второй человек: 24000*1/3=8000 (ливров) 3) Найдем последнюю сумму денег: 24000–12000–8000=4000 (ливров) Ответ: I – 12000 ливров, II – 8000 ливров, III – 4000 ливров.

Задача№54. Задача из тракта «Математика в девяти книгах».

Сообща покупают вещь. Если каждый человек внесет по 8, то избыток (равен) 3. Если каждый человек внесет по 7, то недостаток (равен) 4. Спрашивается количество людей и стоимость вещи.

Решение:

пусть х – количество людей, тогда получим уравнение: 8х – 3=7х+4 Решая уравнение получим, что х=7. тогда стоимость вещи равна 8·7 – 3=53

Ответ: 7 человек, стоимость вещи 53.

Задача №55. Задача из тракта «Математика в девяти книгах».Имеется 5 воробьев и 6 ласточек, их взвесили на весах. вес всех воробьев тяжелее веса всех ласточек. если переместить 1 ласточку и 1 воробья, то вес будет как раз одинаковым. общий вес ласточек и воробьев 1 цзинь. Спрашивается, сколько весят ласточка и воробей.

Решение:

Обозначим за х вес одного воробья и за у вес одной ласточки. Получим систему из двух уравнений: 4х + у = 5у + х и 5х + 6 у = 1 . Знаем, что 5х > 6 у . Решая данные уравнения, имеем х = 2 /19 , у = 3/38 Ответ: вес воробья 2/ 19 цзинь , вес ласточки 3/ 38 цзиня.

Задача 56. Задача Алькуина.

Разделить сто мер пшеницы между сто лицами так , чтобы каждый мужчина получил три , каждая женщина два , а каждое дитя ½ меры. Сколько мужчин , женщин и детей?

Решение.

Составим систему неопределенных уравнений: х+у+с= 100 и 3х+2у+1/2с =100 , где х,у,с- натуральные числа ( мужчины , женщины, дети). Решая данную систему , получим уравнение 2у + 5с= 400. То есть , х= 11, у = 15, с = 74.

--Bookworm ID 213 16:53, 7 ноября 2008 (UZT)

Задачи команды ЛАДА-ВЕКТОР ID_279

Задача № 25

(Анания из Ширака, армянский математик VII века.)

В городе Афинах был водоём, в который проведены 3 трубы. Одна из труб может наполнить водоём в один час, другая, более тонкая, в два часа, третья, ещё более тонкая ,в три часа. Итак, узнай, в какую часть часа все три трубы вместе наполняют бассейн.

Решение:

В 6/11 часа. За 6 ч первая труба наполнит 6 таких водоёмов, вторая -3, а третья-2, всего 11 водоёмов. Значит, 3 трубы вместе наполнят один водоём за 6/11 часа.

Ответ: 6/11 часа.

Задача №26

Задача Адама Ризе ( XVI в.)

26 персон издержали вместе 88 марок, причём мужчина издерживал по 6 марок, женщина - по 4, девушка – по 2. Сколько было мужчин , женщин и девушек?

Решение:

Пусть было m мужчин, g женщин, тогда девушек было 26 - m-g. По условию задачи составим уравнение и упростим его:

6m+4g+2(26-m-g)=88 (6),

2m +g=18 (7).

Так как g делится на 2, подставим g = 2 g₁ (g₁ – натуральное число) в уравнении (7) и упростим его: m + g₁ =9 (8).

Уравнение (8) имеет 8 решений (m;g 1) в натуральных числах(1;8), (2;7), (3;6), (4;5), (5;4), (6;3), (7;2), (8;1). Уравнение (6) тоже имеет 8 решений (m;g) : (1;16), (2;14), (3;12), (4;10), (5;8), (6;6), (7;4), (8;2). Следовательно, задача имеет 8 решений: мужчин, женщин и девушек было 1, 16, 9, или 2, 14, 10, или 3, 12, 11, или 4,10,12, или 5, 8, 13, или 6,6, 14, или 7,4,15, или 8,2, 16.

Задача № 27

Задача Д.Пойа

Торговец продает орехи двух сортов: одни по 90 центов, и другие по 60 центов за килограмм. Он хочет получить 50 кг смеси по 72 цента за килограмм. Сколько для этого потребуется орехов каждого сорта?

Решение:

Пусть было x кг орехов первого сорта и y кг орехов второго сорта, тогда выполняются два равенства:

x+y=50,

90x+60y=3600.

Имеем:

(система)

х + у = 50,

3х + 2у = 120

Для решения систем двух уравнений с двумя переменными применяют один из двух основных способов решения.

1)Способ подстановки.

Выразим y через x из первого уравнения:y=50-x Подставим выражение 50-x во второе уравнение вместо y: 3x +2(50-x)=120, x=20 Теперь найдем y: y=50-20=30.

2)Способ сложения.

Умножим правую и левую части первого уравнения системы (1) на-2 и сложим почленно полученные уравнения:

(система)

- 2х – 2у = - 100,

3х+2у=120.

(система)

х=20,

у=30.

Ответ:20кг первого и 30кг второго сорта.

--Лада-Вектор ID 279 00:12, 9 ноября 2008 (UZT)

Омега ID 276

Занимательные задачи конца 18 века:

1. Во время шторма Во время шторма капитан корабля приказал выбросить за борт половину из 30 тюков с товарами, которые везли два купца. Купцы были в нерешительности: каждому было жаль выбрасывать свой груз. Видя это, капитан сказал: «Сделаем так, матросы расставят 30 тюков по кругу, а мы будем ходить по кругу и выбрасывать каждый 9 тюк, пока не выбросим половину тюков». Один из купцов подкупил матросов, и они сумели расставить тюки так, что 15 оставшихся на палубе тюков оказались с товарами этого купца. Как были расставлены тюки? Решение: Начертим круг и, отметив на нем 30 палочек, поставим у каждой из них номер от 1 до 30. Теперь, начиная счет с цифры 1, перечеркиваем 9 палочку, затем 18, затем 27 и продолжаем этот процесс, вычеркивая каждую девятую из незачеркнутых ранее палочек. Таким образом, будут перечеркнуты палочки с номерами: 5,6,7,8,9,12,16,18,19,22,23,24,26,27,30 Значит, купец попросил расставить тюки следующим образом: 4 своих, 5 чужих, 2 своих, 1 чужой, 3 своих, 1 чужой, 1 свой, 2 чужих, 2 своих, 3 чужих, 1 свой, 2 чужих, 2 своих, 1 чужой. Существует старинный способ запоминания этой последовательности. Необходимо помнить следующие 6 мужских имен: Полуект, Аника, Павел, Елизар, Евтех, Влас. Если под каждой буквой а, встречающейся в этих именах, поставить цифру 1, под каждой буквой е – цифру 2, под каждой буквой и – цифру 3, под каждой буквой о – цифру 4 и под буквой у – цифру 5, то получим: Полуект, Аника, Павел, Елизар, Евтех, Влас. 4 5 2 1 3 1 1 2 2 3 1 2 1 Первая цифра 4 означает число своих тюков, а затем в этой последовательности цифр чередуются количества чужих и своих тюков.

2. Девичья хитрость Золотошвея, взяв 20 девушек в учение, разместила их в 8 комнатах своего дома так, как показано на рисунке.

2 3 2 3 3 2 3 2 По вечерам Золотошвея обходила дом и проверяла, чтобы в комнатах на каждой стороне его было по 7 девушек. Однажды к девушкам в гости приехали 4 подружки и, заговорившись, остались у них ночевать, причем все 24 девушки разместились в комнатах так, что вечером Золотошвея насчитала в комнатах на каждой стороне дома опять по 7 девушек. На следующий день 4 девушки пошли провожать своих четырех подруг и дома не ночевали. Оставшиеся 16 девушек разместились так, что опять вечером Золотошвея насчитала в комнатах с каждой стороны дома по 7 девушек. Как размешались девушки по комнатам в двух последних случаях? Решение: Двадцать четыре девушки можно разместить так, как показано на рисунке 1, а шестнадцать девушек, как показано на рисунке 2.

1 5 1 5 5 1 5 1

        Рисунок 1

3 1 3 1 1 3 1 3

        Рисунок 2

3. Разделить на 8 частей Разделись 46 рублей на 8 частей так, чтобы каждая часть была больше предыдущей на полтинник. Решение: Вторая часть больше первой на один полтинник, третья больше первой на два полтинника, четвертая – на три полтинника и т.д., восьмая часть больше первой на семь полтинников. Сложив числа 1,2,3,…,7, получим 28. Это число полтинников равняется 14 рублям. Значит, если бы все части равнялись первой, то сумма их составила бы 46-14=32 рубля. Поэтому первая часть равна 32:8=4 рубля, вторая часть составляет 4,5 рубля, третья – 5 рублей и т.д., восьмая часть составляет 7,5 рублей.

Участник:ПОБЕДА ID_235

8.Любое число – тремя двойками

ЗАДАЧА

Любое данное число, целое и положительное, изобразить с помощью трех двоек и математических символов.

РЕШЕНИЕ

Покажем, как задача решается, сначала на частном примере. Пусть данное число 3. Тогда задача решается так: Легко удостовериться в правильности этого равенства. Действительности,

Если бы дано было 5, мы разрешили бы задачу тем же приемом:

Как видим, мы используем здесь то, что при квадратном радикале показатель корня не пишется. Общее решение задачи таково. Если данное число N, то Причем число радикалов равно числу единиц в заданном числе.

9.Алгебраические комедии

2*2=5

РЕШЕНИЕ 16 – 36 = 25 – 45 Прибавляются равные числа: 16 – 36 + 20 ¼ = 25 – 45 + 20 ¼ И делаются следующие преобразования:

Затем с помощью незаконного заключения переходят к финалу: 4 – 9/2 = 5 – 9/2, 4 = 5, 2*2=5

МаГмА ID _205

1. Задачи из "Греческой Анталогии":

Ослица и мул шли бок о бок с тяжелой поклажей на спине.Ослица жаловалась на свою непомерно тяжелую ношу."Чего ты жалуешься?-ответил ей мул.-Ведб если я возьму у тебя один мешок, ноша моя станет вдвое тяжелее твоей.А вот если бы ты сняла с моей спины один мешок, твоя поклажа стала бы одинаково с моей".Скоько мешков несла ослица и сколько нес мул?

Решение:

Обозначив через х поклажу ослицы, а через у — поклажу мула, сводим задачу к системе уравнений с двумя неизвестными у + 1 = 2 (х - 1); у — 1 = х + 1 или 2х — у — 3; у — х = 2. Решая эту систему, получаем х = 5, у = 7.

2. Задачи Бхаскары:

Посреди сражения яростный сын Притхи схватил некоторое число стрел,чтобы убить Карну;половину их он употребил на собственную защиту, a учетверенное количество квадратного корня -протв лошадей;6стрел пронзили возницу Салью, 3 других прорвали зонтик Карны,разбили его лук и знамя и только одна последняя пронзила ему голову.Сколько было стрел у Арджуны(сына Притхи)?

Решение:

Уравнение, удовлетворяющее условию задачи, следующее: 0,5х+4 х+6+3+1=х После упрощения получаем х—104х+400 = 0, откуда х = 52± 52 —400 . Следовательно, х = 52 ± 48. Таким образом, имеется два корня: х = 100 и х = 4, причем непосредственной проверкой можно убедиться, что условию задачи удовлетворяет только первый корень.

3. Задачи из "Арифметики" Л.Ф. Магницкого:

Некий человек нанял работника на год, обещав ему дать 12 рублей и кафтан. Но тот по случаю, проработав 7 месяцев, восхотел уйти и просил достойную плату с кафтаном. Ему дали по достоинству 5 рублей и кафтан. Какой цены был оный кафтан?

Решение:

За год работник должен был получить 12 рублен и кафтан, т. е. за каждый проработанный месяц ему должны начислять 1 рубль и 1/12,a стоимости кафтана. За проработанные 7 месяцев работник должен был бы получить 7 рублен и 7/12 стоимости кафтана, а получил 5 рублей и кафтан. Следовательно, 5/12 стоимости кафтана соответствуют 2 рублям. Таким образом, цена кафтана была 2:5/12=2*12/5=24/5=4,8(рубля)

4. Задачи Л.Н.Толстого: Артели косцов надо было скосить два луга, один вдвое больше другого. Половину дня артель косила большой луг. После этого артель разделилась пополам: первая половина осталась на большом лугу и докосила его к вечеру до конца; вторая же половина косила малый луг, на котором к вечеру еще остался участок, скошенный на другой день одним косцом за один день работы. Сколько косцов было в артели?

Решение:

Сам Л. Н. Толстой, по свидетельству проф. А. В. Цингера, решал задачу при помощи следующих рассуждений: «Если большой луг полдня косила вся артель и полдня пол-артели, то ясно, что в полдня полартели скашивает 1/3луга. Следовательно, на малом лугу остался нескошенным участок в1/2-1/3=1/6. Если один косец в день скашивает 1/6 луга, а скошено было6/6+2/6=8/6, то косцов было 8». «Толстой,— вспоминал А. В. Цингер, — всю жизнь любивший фокусные, не слишком хитрые задачи, эту задачу знал от моего отца еще с молодых лет. Когда об этой задаче пришлось беседовать мне с Толстым — уже стариком, его собственно восхитило то, что задача делается гораздо яснее и прозрачнее, если при решении пользоваться самым примитивным чертежом (рис. 48)». Приводим алгебраическое решение задачи. Пусть х— число косцов артели, у — размер участка, скашиваемого одним косцом за 1 день.Заметим, что у — вспомогательное переменное — вводится исключительно для облегчения решения задачи, от него потом освобождаются. Далее, выразим через х и у площади большого и малого луга.Площадь большого луга равняется ху/2+ху/4=3ху/4ху .Площадь малого луга ху/4+у=ху/4+4у/4 Большой луг по условию больше малого в два раза, поэтому (3ху/4):(ху/4)+(4у/4)=2 3ху/ху +4у=2, После сокращения на у получим 3х/(х+4)=2, Откуда х=8.

5. Задачи из "курса Алгебры" А.Н. Страннолюбского:

Два работника прожили у хозяина равное время; один из них получал по 15, а другой по 10 руб. в неделю. При окончательном расчете оказалось, что первый работник должен получить более второго именно на ту сумму, которую он забрал в течение работы, а забрал он сперва 4,5руб., потом 3,5руб. и наконец 7 руб. Сколько недель продолжалась работа?

Решение:

Пусть х — число недель, в течение которых продолжалась работа, тогда (15-10)х=4,5+3,5+7; х=3(недели) --Магма ID 205 18:19, 12 ноября 2008 (UZT)

Совокупность "жареных семечек"ID-224

Из «Введения в анализ бесконечных», т.1, Л. Эйлер

Задача №40

Доказать, что логарифмы двух чисел в любой системе сохраняют одно и то же отношение.

Решение.

(a +blgx)lgx = lgc, пусть lgx = y, тогда by^2 + by – lgc = 0. Найдя y, находим х.

Задача №41

Пусть к концу каждого века число людей удваивается; требуется найти годовой прирост.

Решение.

Если предположим, что число людей возрастает ежегодно на 1/х свою часть, и, притом вначале число людей было равно n, то по истечении 100 лет, это число будет равно [((1+х)/х)^100]*n.

Это должно быть равно 2nи тогда (1+x)/x = 2^1/100, логарифмируем: lg(1+x)/x = 1/100, lg2 = 0,0030103, отсюда (1+х)/х = 10069555/10000000, поэтому х ≈144.

Итак, достаточно ежегодного прироста людей на 1/144 часть.

Задача №42

Пусть число людей увеличивается ежегодно на 1/100 свою часть; спрашивается, через сколько лет число людей удесятериться.

Решение.

Положим, что это наступит через х лет, причем число людей вначале было равно n;

стало быть по истечении х лет оно будет равно [(101/100)^x]*n, а так как оно должно равняться 10n, то

(101/100)^x = 10, xlg(101/100) = lg10, x = lg10/(lg101-lg100) = 1/(lg101-2), x≈231.

Итак, через 231 год число людей, если ежегодное приращение составляет только 1/100 часть, станет больше в 10 раз, отсюда

через 462 года оно станет в 100 раз, а через 693 года в 1000 раз больше.

Задача №43. Задача Ж. Озанама.

Семеро друзей собрались к обеду, но между ними возник спор, кому с кем садиться. Чтобы прекратить пререкания, кто-то из присутствующих предложил всем сесть за стол как придется, но с условием, чтобы в следующие дни обедать вместе, причем каждый раз садиться по разному, до тех пор, пока не будут испробованы все комбинации.

Спрашивается, сколько раз придется им обедать вместе для этой цели?

Решение.

Задача №44. Середина 14 века. Задача Нарайана.

Подсчитать стадо коров и телок, происходящее от одной коровы за 20 лет, по условию корова в начале каждого года рожает телку, а телки дают такое же потомство, достигнув трех лет.

Решение.

В начале 1-го года стадо состояло из 2-х животных, в начале 2-го –из 3-х, затем из 4 и 6.

Начиная с 4-го года численность стада можно выразить рекуррентным соотношением:

S(k) = S(k-1)+S(k-3).

С помощью соотношения последовательно вычисляем S(20) =2745.

Задача №45 Задача о кроликах или числа Фибоначчи

В 1202 году итальянский купец Леонардо из Пизы (1180—1240), более известный под прозвищем Фибоначчи, один из самых значительных математиков средневековья, сформулировал такую задачу:

"Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения."

Рост численности кроликов можно проследить на схеме, выполненной в виде

Задача №46. Китай. «Математический трактат о чжоу-би»

В центре бассейна со стороной 1 чжан = 10 чи растет камыш, выступающий над водой на 1 чи. Оттянутый камыш достигает берега. Какова глубина воды?

Решение.

Сторона бассейна 2а, камыш выступает на высоту h, глубина х.

По теореме Пифагора (х+h)^2 – x^2 = a^2.

(x+1)^2-x^2 = 5^2, 2x+1=25, x=12 (чи)

«Математика в девяти книгах» («Цзю чжан суань шу»

Авторы неизвестны. Лю Хуэй, комментировавший «Математику» в 3 в. , сообщает, что она была составлена по более ранним источникам видным чиновником финансовой службы Чжан Цанем (умер в 152 г. до н.э.)

Задача №47.

В бочке в 10 доу есть неизвестное количество пшена. Бочка дополнена неочищенным просом, и если последнее очистить, то всего получится 7 доу пшена.

Решение.

Запишем уравнение.

х +3/5(10-х)=7 (3/5 – коэффициент перехода от проса к пшену из книги 2 «Математики»)

х = 2,5.

Задача №48.

Наверху стены в 90 цуней растет тыква, стебель которой за день вырастает на 7, внизу растет кабачок, стебель которого вырастает за день на 10. Когда они встретятся?

Решение.

Запишем уравнение (7+10)х = 90.,

х = 90/17=5+5/17 дней.

Задача №49.

Из 3 снопов хорошего урожая, 2 снопов среднего урожая и 1 снопа плохого урожая получили 39 доу. Из двух снопов хорошего урожая, 3 снопов среднего урожая и 1 снопа плохого урожая получили 34 доу. Из 1 снопа хорошего урожая, 2 снопов среднего урожая и 3 снопов плохого урожая получили 26 доу.

Спрашивается, сколько получили из каждого снопа хорошего, среднего и плохого урожая?

Решение.

Весь урожай	Хороший урожай	Средний урожай	Плохой урожай
	В 1-м снопе х доу	В 1-м снопе y доу	В 1-м снопе z доу
39 доу	3 снопа	2 снопа	1 сноп
34 доу	2 снопа	3 снопа	1сноп
26 доу	1 сноп	2 снопа	3снопа

3x+2y+z=39, 2x+3y+z=34, x+2y+3z=26.

x-y=5, x=5+y.

z=34-2(5+y)-3y, z=24-5y.

5+y+2y+(24-5y)*3=26, -12y=26 -77, y=51/12,

y=4+1/4,

X=9+1/4,

z = 2+3/4

Ответ.

Из одного снопа хорошего урожая получается 9,25 доу, из одного снопа среднего урожая получается 4,25 доу, из одного снопа плохого урожая получается 2,75 доу.

Задача №50.

2 снопам хорошего урожая, 3 снопам среднего урожая, 4 снопам плохого урожая не хватает до 1 доу соответственно по 1 снопу среднего урожая, плохого урожая, хорошего урожая.

Спрашивается, сколько получили из каждого снопа хорошего, среднего и плохого урожая?

Решение.

В 1-м снопе хорошего х доу, в 1-м снопе среднего y доу, в 1-м снопе плохого z доу

2х+у =1, 3у+z=1, 4z+x=1.

Y=1-2x, z=1-3y, 4-12(1-2x)+x=1, 25x=9,

x=0,36, y=0,28, z=0,16.

Ответ.

Из одного снопа хорошего урожая получается 0,36 доу, из одного снопа среднего урожая получается 0,28 доу, из одного снопа плохого урожая получается 0,16 доу.

Задача №51.

М.Е. Салтыков-Щедрин

«Порфирий Владимирович сидит у себя в кабинете, исписывая цифирными выкладками листы бумаги. На этот раз его занимает вопрос: сколько было бы теперь денег, если бы маменька подаренные ему при рождении дедушкой на зубок сто рублей не присвоила себе, а положила в ломбард на имя маленького Порфирия? Выходит, однако, немного – всего 800 рублей!»

Решение.

Предполагая, что Порфирию в момент расчета было 50 лет, и, сделав допущения, что Головлев сделал вычисления правильно, требуется установить, по сколько процентов платил в то время ломбард.

800 = 100(1 +p/100)^50

Задача №52.

Старинная задача из сборника Игнатьева Е.В. В царстве смекалки.

Идет крестьянин и плачется: «Эхма! Жизнь моя горькая! Заела нужда совсем! Вот в кармане только несколько медных грошей болтается, да и те нужно отдать. И как это у других получается, что на всякие свои деньги они еще деньги получают? Хоть бы кто помог». Только сказал, глядь, перед ним черт.

«Что ж, - говорит, - помогу. Видишь мост через реку? Как будешь мост переходить, деньги у тебя в кармане удвоятся. Сколько раз перейдешь по мосту, столько раз и удвоятся».

- Ой ли? – удивился крестьянин.

- Верное слово, - сказал черт, - но, чур, уговор! Ты, каждый раз перейдя мост, отдавай мне по 24 копейки. Иначе не помогу.

Согласился крестьянин.

Перешел мост раз. Точно – удвоились деньги. Отдал черту его 24 копейки.

Пошел обратно, опять удвоились. Отсчитал плату черту и перешел третий раз.

Деньги удвоились и их оказалось ровно 24 копейки, которые пришлось отдать черту.

А) Сколько денег было у крестьянина?

Б) Какое минимальное количество денег должно быть у крестьянина, чтобы после третьего перехода и расплаты с чертом деньги у крестьянина удвоились?

Решение.

А) Х – первоначальное количество денег у крестьянина,

2х – после первого перехода,

(2х-24)*2 – после второго перехода,

[(2x-24)*2-24]*2 =24 –после третьего перехода.

(2х – 24)*2=12+24, 2х-24=18, 2х=42, х = 21.

Б) [(2x-24)*2-24]*2 -24= 2х, (2х-24)*2 – 24 =(2х+24)/2, (2х-24)*2 =х+36, 3х=84, х=28.

Ответ. 21 коп., 28 коп.

Задача №53

А. Эйнштейн придумал эту задачу в прошлом веке и полагал, что 98% жителей Земли не в состоянии ее решить.

5 разных человек в 5 разных домах разного цвета, курят 5 разных марок сигарет, выращивают 5 разных видов животных, пьют 5 разных видов напитков.

Вопрос: кому принадлежит рыба?

Алгоритм решения задачи:

Норвежец живет в первом доме

Норвежец живет около голубого дома (2-й)

Жилец из среднего дома пьет молоко (3-й)

Зеленый дом стоит слева от белого

Жилец зеленого дома пьет кофе

Зелёный дом – 4-й

Белый дом – 5-й

Англичанин живет в красном доме

Первый дом – желтый

Норвежец живет в желтом доме

Жилец из желтого дома курит Dunhill

Лошадь у жильца голубого дома

Датчанин пьет чай в голубом доме

Курильщик Winfield пьет пиво в белом доме

Норвежец пьёт воду

Курильщик Marlboro живет в голубом доме (датчанин)

Кошку держит Норвежец

Швед держит собаку в белом доме

Человек, который курит Pallmall, держит птицу – Англичанин

Значит, Немец курит Rothmans и держит рыбу

Задача №54. Жорж Сименон

«Вернувшись домой, Мегре позвонил на набережную Орфевр.

- Говорит Мегре. Есть новости?

- Да, шеф. Поступили сообщения от инспекторов. Торранс установил, что если Франсуа был пьян, то либо Этьен убийца, либо Франсуа лжет. Жуссье считает, что или Этьен убийца или Франсуа не был пьян и убийство произошло после полуночи. Инспектор Люка просил передать Вам, что если убийство произошло после полуночи, то либо Этьен убийца, либо Франсуа лжет. Затем звонила…

- Все. Спасибо. Этого достаточно. Комиссар положил трубку. Он знал, что трезвый Франсуа никогда не лжет. Теперь он знал все».

Решение.

Запишем простые высказывания:

А = { Франсуа пьян}

B = { Этьен убийца }

C = { Франсуа лжет }

D = { убийство произошло после полуночи }

Торранс: A→(B+C) = ┐A+B+C =1

Жуссье: (B+ ┐A)D = BD+ ┐AD =1

Инспектор Люка: D→(B+C) = ┐D+ B+C =1

(┐A+B+C)( BD+ ┐AD)( ┐D+ B+C) = 1

(BD┐A + BD B + BD C+ ┐AD┐A + ┐AD B + ┐ADC)( ┐D+ B+C)= 1

Применяя закон поглощения: (┐AD+BD) ( ┐D+ B+C)= ┐AD┐D + ┐ADB +┐ADC+ BD┐D + BDD+ BDC= ┐ADB + ┐ADC+BD+ BDC= BD+ ┐ADC

Известно, что трезвый Франсуа никогда не лжет, значит ┐ADC=0

Итак, BD=1

Ответ: Этьен убийца и убийство произошло после полуночи

--"Жареные семечки" 23:31, 9 ноября 2008 (UZT)

'Задача №55.'Задача Пуассона.

Как из полного сосуда ёмкостью в 12 л отлить половину, пользуясь двумя пустыми сосудами ёмкостью в 8 и 5 л?

Ответ:

Сначала наливаете 8 литров в 8л., потом из 8л. наливаете полный 5л., в результате получается, что в 12л. - 4 литра, в 8л - 3литра, а в 5л. - 5 литров.

Переливаете из 5л. в 12л. всю воду (или что там за жидкость), а из 8л. переливаете все 3 литра в 5л. В результате 9 литров в 12л, 0 литров в 8л., и 3 литра в 5л.

Переливаете из 12л. 8 литров в пустой 8л.,и в 12 л. остается 1 литр.

Из 8л. доливаете в 5л., пока 5л. не станет полным, (в 5л. было 3л., след. долили мы еще 2литра из 8л.)

Тогда в 8л. как раз остается 6л.

--"Жареные семечки" 00:45, 13 ноября 2008 (UZT)

Омега ID 276

Занимательные задачи конца 18 века:

1. Во время шторма Во время шторма капитан корабля приказал выбросить за борт половину из 30 тюков с товарами, которые везли два купца. Купцы были в нерешительности: каждому было жаль выбрасывать свой груз. Видя это, капитан сказал: «Сделаем так, матросы расставят 30 тюков по кругу, а мы будем ходить по кругу и выбрасывать каждый 9 тюк, пока не выбросим половину тюков». Один из купцов подкупил матросов, и они сумели расставить тюки так, что 15 оставшихся на палубе тюков оказались с товарами этого купца. Как были расставлены тюки? Решение: Начертим круг и, отметив на нем 30 палочек, поставим у каждой из них номер от 1 до 30. Теперь, начиная счет с цифры 1, перечеркиваем 9 палочку, затем 18, затем 27 и продолжаем этот процесс, вычеркивая каждую девятую из незачеркнутых ранее палочек. Таким образом, будут перечеркнуты палочки с номерами: 5,6,7,8,9,12,16,18,19,22,23,24,26,27,30 Значит, купец попросил расставить тюки следующим образом: 4 своих, 5 чужих, 2 своих, 1 чужой, 3 своих, 1 чужой, 1 свой, 2 чужих, 2 своих, 3 чужих, 1 свой, 2 чужих, 2 своих, 1 чужой. Существует старинный способ запоминания этой последовательности. Необходимо помнить следующие 6 мужских имен: Полуект, Аника, Павел, Елизар, Евтех, Влас. Если под каждой буквой а, встречающейся в этих именах, поставить цифру 1, под каждой буквой е – цифру 2, под каждой буквой и – цифру 3, под каждой буквой о – цифру 4 и под буквой у – цифру 5, то получим: Полуект, Аника, Павел, Елизар, Евтех, Влас. 4 5 2 1 3 1 1 2 2 3 1 2 1 Первая цифра 4 означает число своих тюков, а затем в этой последовательности цифр чередуются количества чужих и своих тюков. 2. Девичья хитрость Золотошвея, взяв 20 девушек в учение, разместила их в 8 комнатах своего дома так, как показано на рисунке.

2 3 2 3 3 2 3 2 По вечерам Золотошвея обходила дом и проверяла, чтобы в комнатах на каждой стороне его было по 7 девушек. Однажды к девушкам в гости приехали 4 подружки и, заговорившись, остались у них ночевать, причем все 24 девушки разместились в комнатах так, что вечером Золотошвея насчитала в комнатах на каждой стороне дома опять по 7 девушек. На следующий день 4 девушки пошли провожать своих четырех подруг и дома не ночевали. Оставшиеся 16 девушек разместились так, что опять вечером Золотошвея насчитала в комнатах с каждой стороны дома по 7 девушек. Как размешались девушки по комнатам в двух последних случаях? Решение: Двадцать четыре девушки можно разместить так, как показано на рисунке 1, а шестнадцать девушек, как показано на рисунке 2.

1 5 1 5 5 1 5 1

        Рисунок 1

3 1 3 1 1 3 1 3

        Рисунок 2

3. Разделить на 8 частей Разделись 46 рублей на 8 частей так, чтобы каждая часть была больше предыдущей на полтинник. Решение: Вторая часть больше первой на один полтинник, третья больше первой на два полтинника, четвертая – на три полтинника и т.д., восьмая часть больше первой на семь полтинников. Сложив числа 1,2,3,…,7, получим 28. Это число полтинников равняется 14 рублям. Значит, если бы все части равнялись первой, то сумма их составила бы 46-14=32 рубля. Поэтому первая часть равна 32:8=4 рубля, вторая часть составляет 4,5 рубля, третья – 5 рублей и т.д., восьмая часть составляет 7,5 рублей.

--Bookworm ID 213 13:36, 11 ноября 2008 (UZT) Задача№57. Задача Л. Эйлера. Некто продает свою лошадь по числу подкованных гвоздей, которых у неё 32. За первый Гвоздь он просит 1 коп., за второй 2, за третий 4, за четвертый 8 и всегда за следующий вдвое больше, чем за предыдущий. Спрашивается, во сколько он ценит свою лошадь? Решение: Имеем геометрическую прогрессию. Нас просят найти сумму всех гвоздей. Для решения задачи применим формулу для расчетов суммы n членов прогрессии: Sn=b1(1–qn)/1-q, где b1=1, n=32, q=2. Получим: S32=1(1–232)/1-2=4294967295 (копеек) Ответ: 4294967295 копеек, или 42949672 рубля 95 копеек.

Задача №58. Задача из книг новгородских писцов. В книгах новгородских писцов XVв. упоминаются такие меры жидкостей: бочка, насадка и ведро. Из этих же книг стало известно, что 1 бочка и 20 ведер кваса уравниваются с тремя бочками кваса, а 19 бочек, 1 насадка и 15,5 ведра уравниваются с 20 бочками и 8 ведрами. Можно ли на основании этих данных определить, сколько насадок содержится в бочке? Решение: Обозначим емкости бочки, насадки и ведра равны соответственно x,y,z. Тогда получим систему уравнений: x+20z=3x и 19x+ y+15,5z=20х+8z Решая систему, получим х=4у т. е. в одной бочке содержится 4 насадки. Ответ: В одной бочке содержится 4 насадки.

Задача №59. Задача из «Счетной мудрости». Идет корабль по морю, на нем мужеска полу и женска 120 человек. Найму дали 120 гривен, мущины дали по 4 алтына, а женщины дали по 3 алтына с человека. Сколько мужеска полу было женска порознь? (Гривна, гривенник – десять копеек, алтын равнялся 3 копейкам.) Решение: Число мужчин: (1200–120*9)/(12–9)=40 Число женщин 120–40=80 Ответ: мужчин было 40 человек, женщин было 80 человек.

Задача №60. Задача из рукописи XVII в. Четыре плотника у некого гостя нанялись двора ставити. И говорит первый плотник так: «Только б де мне одному тот двор ставити, я бы де его поставил един годом». А другой молвил: «Только б де мне одному тот двор ставити, и я бы де его поставил в два года». Третий молвил: «Только б де мне одному тот двор ставити, и я бы де его поставил в три года». А четвертый так рёк: «Только б де мне одному тот двор ставити, и я бы де его поставил в четыре года». Ино все те четыре плотника учали тот двор ставити вместе. Ино сколь долго они ставили, сочти мне. Решение: За 12 лет первый плотник построит 12 дворов, второй–6; третий–4; четвертый–3. Следовательно, за 12 лет они вместе построят 25 дворов. Таким образом, четыре плотника вместе один двор построят за (365*12)/25=175,2 дня. Ответ: за 175,2 дня.

Задача № 61. Задача Эйлера. Некий чиновник купил лошадей быков за 1770 талеров. За каждую лошадь он уплатил по 31 талеру, а за каждого быка – по 21 талеру. Сколько лошадей и быков купил чиновник? Решение: Если х – число лошадей, у – число быков, то 31х+21у=1770 откуда у=84-х-(10х-6)/21 Из последнего равенства следует, что (5х-3) делится на 21. Обозначив 5х-3=21z, получим у=84-х-2z и х=4z+(z+3)/5. Следовательно, (z+3) делится на 5, т.е. z=5t-3, x=21t-12 и y=102-31t.Так как y>0 и z=5t-3≠0, то t1=1, t2=2, t3=3 соответственно x1=9, y1=71; x2=30, y2=40; x3=51, y3=9.

Задача №62. Задача Кирика Новгородца. Сколько месяцев, недель, дней и часов прожил человек, которому в 1136 г. исполнилось 26 лет? Решение: месяцы – 26 * 12 = 312, недели – 26 * 52 = 1356, дни - 26 * 365 = 9497, часы – 9497 * 24 = 227928. Ответ: человек прожил 26 лет, 312 месяцев, 1356 недель, 9497 дней, 227928 часов.

Задача №63. Французская задача. Трое имеют по некоторой сумме денег каждый. Первый даёт из своих денег двум другим столько, сколько есть у каждого. После него второй даёт двум другим столько, сколько каждый из них имеет. Наконец, третий даёт двум другим столько, сколько есть у каждого. После этого у всех троих оказывается по 8 экю (монет). Спрашивается, сколько денег было у каждого вначале. Ответ: I 8 8/2 = 4 4/2 = 2 2+14/2+8/2 = 13 II 8 8/2 = 4 4+4/2+16/2 = 14 14/2 = 7 III 8 8+8/2+8/2=16 16/2 = 8 8/2 = 4

Значит, сначала у каждого было 13, 7, 4 экю.

Задача №64. Задача Ризе. Трое торгуют лошадь за 12 флоринов, но никто в отдельности не располагает такой суммой. Первый говорит двум другим: «Дайте мне каждый по половине своих денег, и я куплю лошадь». Второй говорит первому и третьему: «Дайте мне по одной трети ваших денег, и я приобрету лошадь». Наконец, третий говорит первым двум: «Дайте мне только по одной четверти ваших денег, и лошадь будет моя». Теперь спрашивается, сколько денег было у каждого. Ответ: Пусть x, y, z – количество флоринов соответственно у первого, второго и третьего покупателей. Решение системы уравнений: x+1/2(y+y) = 12 и y+1/3(x+z) = 12 и z+1/4(x+y) = 12 Даёт нам: x = 3 9/17, y = 7 13/17, z = 9 3/17 флоринов.

Задача №65. Задача Пизанского. Некто поместил пару кроликов в некоем месте, огороженным со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течение года. Причём природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождаются кролики со второго месяца. Ответ: От одной пары кроликов в год родится: 1+1+2+3+5+8+13+21+34+55+89+144 = 376 Эта задача приводит к ряду Фибоначе: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…

Задача №66. Задача Пизанского. Один говорит другому: «Дай мне 7 динариев, и я буду в 5 раз богаче тебя». А другой говорит: «Дай мне 5 динариев, и я буду в 7 раз богаче тебя». Сколько у каждого? Ответ: Решив систему уравнений: x+7 = 5(y-7) и y+5 = 7(x-5) Получим, что первый имел x = 7 2/17 динариея, а второй y = 9 14/17 динария.

Задача №67. Задача Пизанского. Выбрать 5 гирь так, чтобы с их помощью можно было взвесить любой груз от 1 до 30 целых весовых единиц. Все гири при взвешивании разрешается ставить только на одну и туже чашку весов. Ответ: Если m1, m2, m3, m4, m5 – массы гирь, то масса m=< 30 весовых единиц любого груза необходимо представить в виде. m = a1m1+a2m2+a3m3+a4m4+a5m5 где коэффициенты a1, a2, a3, a4, a5 равны либо 0, либо 1. Массы гирь m1, m2, m3, m4, m5 достаточно выбрать равными 1, 2, 4, 8, 16 весовым единицам, так как сумма масс равна 31, что больше 30. Любое число --Bookworm ID 213 13:36, 11 ноября 2008 (UZT)

Участник: Максимум ID_251

ДЕЛЕЖ ВЕРБЛЮДОВ

Старик, имевший трех сыновей, распорядился, чтобы они после его смерти поделили принадлежавшее ему стадо верблюдов так, чтобы старший взял половину всех верблюдов, средний — треть и младший - девятую часть всех верблюдов. Старик умер и оставил 17 верблюдов. Сыновья начали дележ, но оказалось, что число 17 не делится ни на 2, ни на 3, ни на 9. В недоумении, как им быть, братья обратились к мудрецу. Тот приехал к ним на собственном верблюде и разделил по завещанию. Как он сделал?

Решение.

Мудрец пустился на уловку. Он прибавил к стаду на время своего верблюда, тогда их стало 18. Разделив это число, как сказано в завещании (старший брат получил 18 = 9 верблюдов; средний 18 = 6 верблюдов, младший 18 = 2 верблюда), мудрец взял своего верблюда обратно 9+6+2+1=18). Секрет, как и в предыдущей задаче, заключается в том, что части, на которые по завещанию должны были делить стадо сыновья, в сумме не составляют 1.

 КРЕСТЬЯНЕ И КАРТОФЕЛЬ

Шли три крестьянина и зашли на постоялый двор отдохнуть и пообедать. Заказали хозяйке сварить картофель, а сами заснули. Хозяйка сварила картофель, но не стала будить постояльцев, а поставила миску с едой на стол и ушла. Проснулся один крестьянин, увидел картофель и, чтобы не будить товарищей, сосчитал картофель, съел свою долю и снова заснул. Вскоре проснулся другой; ему невдомек было, что один из товарищей уже съел свою долю, поэтому он сосчитал весь оставшийся картофель, съел третью часть и опять заснул. После него проснулся третий; полагая, что он проснулся первым, он сосчитал оставшийся в чашке картофель и съел третью часть. Тут проснулись его товарищи и увидели, что в чашке осталось 8 картофелин. Тогда только объяснилось дело. Сосчитайте, сколько картофелин подала на стол хозяйка, сколько съел уже и сколько должен еще съесть каждый, чтобы всем досталось поровну.

Решение.

Третий крестьянин оставил для товарищей 8 картофелин, т. е. каждому по 4 штуки. Значит, и сам он съел 4 картофелины. После этого легко сообразить, что второй крестьянин оставил своим товарищам 12 картофелин, но 6 на каждого, значит, и сам съел 6 штук. Отсюда следует, что первый крестьянин оставил товарищам 18 картофелин, по 9 штук на каждого, значит, и сам съел 9 штук. Итак, хозяйка подала на стол 27 картофелин, и на долю каждого поэтому приходилось по 9 картофелин. Но первый крестьянин всю свою долю съел. Следовательно, из восьми оставшихся картофелин приходится на долю второго 3, а на долю третьего 5 штук.

 Сколько было?

Женщина несла для продажи корзину яиц. Встретившийся прохожий по неосторожности так толкнул ее, что корзина упала на землю и все яйца разбились. Прохожий захотел уплатить женщине стоимость разбитых яиц и спросил, сколько их всего было. «Я не помню, - сказала женщина, — знаю только хорошо, что когда я перекладывала яйца по 2, то оставалось 1 яйцо. Точно так же всегда оставалось по 1 яйцу, когда я перекладывала их по 3, по 4, по 5 и по 6. Когда же я перекладывала их по 7, то не оставалось ни одного яйца». Спрашивается, сколько было яиц?

Решение.

Задача, очевидно сводится к нахождению такого числа, которое делится без остатка на 7, а при делении на 2, 3,4, 5 и 6 дает в остатке 1. Наименьшее число, которое делится без остатка на 2, 3, 4, 5 и 6 (наименьшее кратное этих чисел), есть 60. Нужно, значит, найти такое число, которое делилось бы на 7 без остатка и было бы вместе с тем на 1 больше числа, делящегося на 60. Такое число можно найти путем последовательных попыток: 60, деленное на 7, дает в остатке 4, следовательно, 2 х 60 дает в остатке 1 (2x4 = 8; 8-7=1). Значит, 2 х 60 = числу, кратному 7 + 1, отсюда следует, что (7 х 60 - 2 х 60) + 1 = числу, кратному 7, т.е. 5 х 60 + 1 = числу, кратному 7, 5 х 60 + 1 = 301. Итак, наименьшее число, решающее задачу, есть 301. То есть наименьшее число яиц, которое могло быть в корзине у женщины, есть 301.

 Задача Чжан Цюцзяня (V в.)

1 петух стоит 5 цяней, 1 курица стоит 3 цяня, 3 цыпленка стоят 1 цянь. Всего на 100 цяней купили 100 птиц. Спрашивается, сколько было в отдельности петухов, кур, цыплят.

Решение

Решение системы сводится к следующим уравнениям: y = 25 - 7/4 x, z = 75 - 3/4 x. Задавая значения х=0;4;8;12, получим решения задачи: (0;25;75), (4;18;78), (8;11;81), (12; 4; 84).

 Задачи из папируса Ахмеса.

1. Раздели 10 мер хлеба на 10 человек, если разность между количеством хлеба у каждого человека и ему предшествующего составляет 1/8 меры.

Решение

10 мер хлеба автор разлагает на 10 членов арифметической прогрессии с разностью 1\8 и получает, что 10-й член прогрессии равен 1+9*1/2*1/8=25/16.

2. Найти приближенное значение для числа ,приняв площадь круга равной площади квадрата со стороной 8/9 диаметра круга.

Решение

По условию задачи (8/9 d)^2=пd^2/4. Тогда п=3,1604.

--Максимум ID 251 15:58, 11 ноября 2008 (UZT)

Участник:Модные переменные_ID_222

Задача Л.Ф. Магницкого

Некий человек нанял работника на год, обещая ему дать 12 р. и кафтан, но тот проработав 7 месяцев, восхотел уйти и просил достойной платы с кафтаном; он же даде ему по достоинству расчёт 5 р. и кафтан, и ведательно есть, коликой цены оный кафтан был.

Решение

Пусть х р. - стоимость кафтана, тогда можно составить уравнение

7(1+х/12)=5+х.

х=24/5

х=4,8

Ответ: кафтан стоит 4 р. 80 коп.

Задача из Математических рукописей 17 в.

Вол съел копну одним часом, а конь съел копну в два часа, а коза съела копну в три часа.Сколько бы они скоро, все три - вол, конь и коза - ту копну съели, сочти.

Решение

За 12 ч вол съест 12 копен, конь - 6, коза - 4, всего они съели 22 копны за 12 ч. Поэтому одну копну вол, конь и коза вместе съедят за 12/22=6/11 ч.

Ответ: вместе вол, конь и коза съедят копну за 6/11 ч.

--Модные переменные ID 222 00:46, 12 ноября 2008 (UZT)

--Bookworm ID 213 11:07, 12 ноября 2008 (UZT) Задача №68. Задача Магавиры (Индия). Найти число павлинов в стае, 1/16 которой, умноженная на себя, сидит на манговом дереве, а квадрат 1/9 остатка вместе с 14 другими павлинами – на дереве тамала. Решение: ((1/16)2+(152/92*162))x2+14 = x Где х - число павлинов в стае. Отсюда x1 = 48, а x2 = 336/17 не подходит.

Задача №69. Задача Магавиры (Индия). О друг, назови число различных ожерелий, которые можно получить из бриллиант, сапфиров, изумрудов, кораллов и жемчугов. Решение: С15+ С25+ С35+ С45+ С55 = (1+1)5+14 = 31 Ответ: 31

Задача №70. Задача Ариабхаты (Греция). Два лица имеют равные капиталы, причём каждый состоит из известного числа вещей одинаковой ценности и известного числа монет. Но как число вещей, так и суммы денег у каждого различны. Какова ценность вещи? Решение: Задача сводится к решению уравнения: ax+b = cx+d, откуда x = (d-b)/(a-c), где у первого лица будет a вещей и b монет, а у второго лица – c вещей и d монет

Задача №71. Задача Сунь-цзы (Китай). Имеются вещи, число их неизвестно. Если считать их тройками, то остаток 2; если считать их пятёрками, то остаток 3; если считать их семёрками, то остаток 2. Спрашивается, сколько вещей. Решение: 23+105t, где t – целое, неотрицательное число.

Задача №72. Задача Дидоны (Греция). Участок земли какой формы окружила Дидона верёвкой данной длины, чтобы получить наибольшую площадь? Решение: Решение задачи Дидоны легко и красиво следует из изопериметрического свойства круга: среди всех плоских фигур данного периметра максимальную площадь имеет круг. Это замечательно свойство было известно в Древней Греции. Поэтому Дидона окружила имевшийся верёвкой участок земли в форме полукруга с центром на берегу моря.

Задача №73. Задача Фалеса (Греция). Определить расстояние от берега до корабля на море. Решение: Для определения расстояния от точки А на берегу до недоступной точки В (местонахождение корабля на море) строим треугольник ABC с доступной точкой С на берегу, после чего отрезки АС и ВС продолжались по другую сторону точки С и строился треугольник CDE, такой, что CD = AC, ∟ACB = ∟DCE и ∟CDE = ∟CAB. Тогда по теореме о равенстве двух треугольников имеющих сторону и два угла, получаем AB = DE

Задача №74. Задача о статуе Минервы. Я – изваянье из злата. Поэты то злато В дар принесли: Харизий принёс половину всей жертвы, Феспия часть восьмую дала; десятую - Солон. Часть двадцатая – жертва певца Фемисона, а девять Всё завершивших талантов – обет, Аристоником данный. Сколько же злата поэты вместе в дар принесли? Решение: Узнаем, какую часть от всех даров, составляет обет Аристоника: 1-(1/2+1/8+1/10+1/20)=9/40. Затем найдем количество золота, которое принесли все поэты вместе: 9/(9/40)=40. Ответ: 40.

Задача №75. Задача о Грациях (Греция). Три грации имели по одинаковому числу плодов и встретили девять муз. Каждая из граций отдала каждой из муз по одинаковому числу плодов. После этого у каждой из муз и каждой грации стало по одинаковому числу плодов. Сколько плодов было у каждой грации до встречи с музами? Решение: Пусть у каждой грации было по х плодов, и они отдали каждой из муз по у плодов. Тогда по условию задачи должно быть: х-9у = 3у или х = 12у Т.е. у каждой из граций до встречи с музами было число плодов кратно 12. Ответ: у каждой из граций до встречи с музами было число плодов кратно 12. --Bookworm ID 213 11:07, 12 ноября 2008 (UZT)

Совокупность "жареных семечек"

Задачи из книги Р. Смаллиана "Как же называется эта книга?"

Задача №56

На чей портрет я смотрю?

Когда я был маленьким, эта головоломка пользовалась необычайной популярностью. Сейчас она менее известна. Эта головоломка обладает одной замечательной особенностью: большинство людей дают неправильный ответ на вопрос задачи, но вопреки всем аргументам упрямо отстаивают свое решение. Помню, однажды лет 50 тому назад в одной компании разгорелся многочасовой спор по поводу этой головоломки, но тем, кто верно решил ее, так и не удалось убедить остальных в правильности полученного решения. Вот эта головоломка.

Человек разглядывает портрет. "Чей это портрет вы рассматриваете?" - спрашивают у него, и человек отвечает: "В семье я рос один, как перст, один. И все ж отец того, кто на портрете, - сын моего отца (вы не ослышались, все верно - сын!)". Чей портрет разглядывает человек?

Ответ:

Удивительно, как много людей дают неверный ответ на вопрос этой головоломки. Они мысленно ставят себя на место человека, разглядывающего портрет, и рассуждают следующим образом: "Так как у меня нет ни братьев, ни сестер, то сыном моего отца могу быть я сам и никто другой. Следовательно, я смотрю на свой собственный портрет".

Первое утверждение абсолютно правильно: если у меня нет ни братьев, ни сестер, то сыном моего отца могу быть только я сам. Но отсюда отнюдь не следует, будто правильный ответ на вопрос задачи гласит: "Самого себя". Так можно было бы ответить, если бы во второй посылке стояло "и все же тот, кого мы видим на портрете, - сын моего отца". Но в условии задачи этого не говорится. Там утверждается, что "отец того, кто на портрете, - сын моего отца". Отсюда следует, что отец человека на портрете - я сам (так как я единственный сын своего отца). Поскольку я отец человека на портрете, то он должен быть моим сыном. Следовательно, правильный ответ состоит в том, что человек разглядывает портрет своего сына.

Если мои рассуждения не убедили скептически настроенного читателя (а я уверен, что многие из читателей не согласны с моими аргументами!), то их можно представить в более наглядном виде.

(1) Отец человека на портрете - сын моего отца.

Подставляя краткое "я" вместо более громоздкого выражения "сын моего отца", преобразуем утверждение (1) к следующему:

(2) Отец человека на портрете - я.

Теперь вы убедились, дорогой читатель?

Задача №57

2. Предположим, что в предыдущей задаче человек, разглядывающий портрет, ответил на вопрос так: "В семье я рос один; как перст, один. И все же сын того, кто на портрете, - сын моего отца (вы не ослышались, все верно - сын!)".

Чей портрет разглядывает этот человек?

Ответ: B этом случае человек разглядывает портрет своего отца.

Задача №58

3. Что произойдет, если всесокрушающее пушечное ядро попадет в несокрушимый столб? Вот еще одна головоломка времен моего детства, которая мне очень нравится. Под всесокрушающим пушечным ядром мы понимаем ядро, сметающее на своем пути все, что попадается, а под несокрушимым столбом - столб, который нельзя ни повалить, ни сломать.

Что произойдет, если всесокрушающее пушечное ядро попадает в несокрушимый столб?

Ответ: При заданных условиях задача логически противоречива: всесокрушающее пушечное ядро и несокрушимый столб не могут существовать одновременно. Если бы существовало всесокрушающее пушечное ядро, то оно по определению сшибало бы на своем пути любой столб. Следовательно, в этом случае не мог бы существовать несокрушимый столб. Наоборот, если бы существовал несокрушимый столб, то по определению его не могло бы сбить ни одно пушечное ядро. Следовательно, в этом случае не могло бы существовать всесокрушающее пушечное ядро. Таким образом, существование всесокрушающего пушечного ядра само по себе не приводит к логическому противоречию. Существование несокрушимого столба само по себе также вполне допустимо. Но утверждение о том, что всесокрушающее пушечное ядро и несокрушимый столб существуют одновременно, противоречиво.

По существу деле обстоит так, как если бы я спросил у вас: "Живут на свете два человека - Джон и Джек. Джон ростом выше Джека, а Джек выше Джона. Как, по-вашему, это может быть?" Лучший ответ, который вы могли бы дать в этом случае, гласил бы: "Вы либо лжете, либо ошибаетесь".

Задача №59

4. Следующая очень простая задача - одна из многочисленных занимательных задач, снискавших широкую известность. В темной комнате стоит шкаф, в ящике которого лежат 24 красных и 24 синих носка. Сколько носков следует взять из ящика, чтобы из них заведомо можно было составить по крайней мере одну пару носков одного цвета? (В этой и в следующей задаче речь идет о наименьшем числе носков.)

Ответ:

Обычно на вопрос задачи дают неправильный ответ: 25 носков. Если бы в задаче спрашивалось, сколько носков следует взять из ящика, чтобы среди них было по крайней мере 2 носка различного цвета, то правильный ответ действительно был бы таким: 25 носков. Но в нашей задаче речь идет о том, чтобы среди взятых из ящика носков по крайней мере 2 носка были одного цвета, поэтому правильный ответ задачи иной: 3 носка. Если я возьму из ящика 3 носка, то они либо все будут одного цвета (и в этом случае я заведомо смогу выбрать из них по крайней мере 2 носка одного цвета), либо 2 носка будут одного цвета, а третий носок другого, что позволит мне также составить пару одноцветных носков.

Задача №60

5. Новый поворот в предыдущей задаче.

Предположим, что в ящике шкафа лежат несколько синих и столько же красных носков. Известно, что минимальное число носков, которые я должен взять из ящика, чтобы из них заведомо можно было составить по крайней мере одну пару носков одинакового цвета, совпадает с минимальным числом носков, которые требуется взять из ящика, чтобы из них можно было составить по крайней мере одну пару носков разного цвета. Сколько носков в ящике?

Ответ: В ящике 4 носка.

Задача №61

6. Вот многим знакомая логическая задача. Известно, что в Нью-Йорке жителей больше, чем волос на голове у любого из них, и что среди жителей Нью-Йорка нет полностью лысых, у которых на голове не осталось бы ни одного волоса. Следует ли отсюда, что в Нью-Йорке непременно найдутся по крайней мере два жителя с одинаковым числом волос на голове?

Приведем еще один вариант этой задачи, незначительно отличающийся от предыдущего. О населении города Поданк известно следующее.

Среди жителей Поданка не найдется двух с равным числом волос на голове. Ни у одного жителя Поданка на голове не растет ровно 518 волос. Жителей в Поданке больше, чем волос на голове любого из них. Какова наибольшая численность населения Поданка?

Ответ: На вопрос первой задачи ответ утвердительный.

Предположим для определенности, что население Нью-Йорка составляет 8 миллионов человек. Если число волос на голове у каждого жителя Нью-Йорка неповторимо, то это означает, что должно существовать 8 миллионов различных целых положительных чисел, каждое из которых меньше 8 миллионов, а это невозможно.

Переходим ко второй задаче. Численность населения Поданка не превышает 518 человек. Действительно, предположим, что в городе Поданк проживает более 518 человек - например, 520 человек. В этом случае должны были бы существовать 520 различных целых неотрицательных чисел, отличных от 518 и меньших 520. Но это невозможно, так как существует ровно 520 целых чисел (и среди них нуль), каждое из которых меньше 520. Следовательно, существует лишь 519 чисел, отличных от 518, которые меньше 520.

Заметим, кстати, что один из жителей Поданка должен быть совершенно лысым. Почему?

Задача №62

7. Кто убийца?

В этой истории речь пойдет о караване, идущем через пустыню Сахару. Однажды караван остановился на ночлег. Обозначим трех главных действующих лиц A, B и C. A ненавидел C и решил убить его, подсыпав яду в бурдюк с питьевой водой (единственным запасом воды, которым располагал C). Независимо от A другой караванщик B также решил убить C и (не зная, что принадлежащая тому питьевая вода уже отравлена) проделал в бурдюке крохотную дырочку, чтобы вода потихоньку вытекала. Через несколько дней C умер от жажды.

Спрашивается, кто убийца? A или B?

Одни считают убийцей караванщика B, поскольку C все равно не успел принять яд, подсыпанный его недругом A, и умер бы, даже если бы A не отравил воду. Другие считают убийцей караванщика A, так как, по их мнению, действия караванщика B не оказали ни малейшего влияния на исход событий: коль скоро A отравил воду, C обречен и умер бы, даже если бы другой его недруг B не проделал дырочку в бурдюке с водой. Чьи рассуждения правильны?

В связи с нашей задачей я вспомнил анекдот о лесорубе, который в поисках работы забрел в лагерь лесозаготовителей. Управляющий встретил его не слишком обнадеживающе. "Не знаю, подойдет ли тебе работа, - сказал он. - Мы здесь валим лес". Лесоруб обрадовался: "Эта работа как раз по мне". Управляющий решил испытать его в деле. "Вот топор, - сказал он. - Посмотрим, сколько времени потребуется тебе, чтобы свалить вон то дерево". Лесоруб бросился к дереву и свалил его одним ударом топора. Управляющий был потрясен, но не сдавался. "Великолепно, - сказал он, - а теперь попробуй повалить вон то большое дерево". Лесоруб подошел к огромному дереву и двумя ударами - трах, бах! - повалил и его. "Невероятно! - воскликнул управляющий. - B жизни не видал ничего подобного. Вы, конечно, приняты! Но где вы научились так валить лес?" "Я изрядно попрактиковался и набил руку в лесу Сахары", - ответил лесоруб. Управляющий на миг задумался. "Вы хотели сказать "в пустыне Сахаре?" - переспросил он. "Теперь там пустыня", - пояснил лесоруб.

Ответ: Не думаю, чтобы рассуждения сторонников любого из двух мнений относительно того, кто убийца, можно было считать "правильными" или "неправильными". В проблемах подобного типа, как мне кажется, одно мнение ничем не хуже и не лучше другого. Лично я считаю, что если кого-нибудь и обвинять в смерти караванщика C, то его недруга A. Если бы я был защитником караванщика B, то обратил бы внимание суда на два обстоятельства: 1) лишить человека отравленной воды не означает убить его; 2) в любом случае действия караванщика B способствовали продлению жизни караванщика C (хотя это и не входило в намерения караванщика B), поскольку смерть от отравления наступила бы быстрее, чем смерть от жажды.

Защитник караванщика A мог бы возразить мне: "Как можно, находясь в здравом уме, обвинять моего подзащитного в отравлении, если C в действительности не выпил ни капли яда?" Как видите, мы столкнулись с поистине головоломной проблемой. Дело усложняется тем, что проблему можно рассматривать с точки зрения морали, права и подходить к ней с чисто научных позиций, используя такое понятие, как причинность. С точки зрения морали и A, и B виновны в том, что замышляли убийство, но наказание за совершенное убийство по строгости не сравнимо с наказанием за преступный замысел. Правовая оценка этого дела мне не известна. Думаю, что приговоры, вынесенные различными составами присяжных, не были бы одинаковыми. Что же касается научного подхода к решению нашей головоломки, то само понятие причинности затрагивает множество проблем.

Задача №63

8. Еще один юридический казус.

Двоих судили за убийство. Присяжные признали одного из обвиняемых виновным, а другого невиновным. Судья обратился к тому, кто был признан виновным, и сказал: "Это самое странное дело из всех, которые мне приходилось разбирать. Хотя ваша вина вне всяких сомнений установлена, по закону я должен выпустить вас на свободу".

Как объяснить столь неожиданное заявление судьи?

Ответ: Обвиняемые были сиамскими близнецами.

Задача №64

9. Двое краснокожих.

Двое краснокожих сидели на бревнышке, один повыше ростом, другой пониже. Тот, кто пониже ростом, доводится сыном тому, кто повыше ростом, хотя тот, кто повыше ростом, - не его отец. Как вы это объясните?

Ответ: Тот из краснокожих, кто повыше ростом, - мать того, кто ростом пониже.

Задача №65

10. Часы остановились. Вот превосходная старинная задача-головоломка. У одного человека не было наручных часов, но зато дома висели точные настенные часы, которые он иногда забывал заводить. Однажды, забыв в очередной раз завести часы, он отправился в гости к своему другу, провел у того вечер, а вернувшись домой, сумел правильно поставить часы. Каким образом ему удалось это сделать, если время в пути заранее известно не было?

Ответ: Выходя из дома, человек заводит часы и запоминает, в каком положении находятся стрелки. Придя к другу и уходя из гостей, он отмечает время своего прихода и ухода. Это позволяет ему узнать, сколько он находился в гостях. Вернувшись домой и взглянув на часы, человек определяет продолжительность своего отсутствия. Вычитая из этого времени то время, которое он провел в гостях, человек узнает время, затраченное на дорогу туда и обратно. Прибавив ко времени выхода из гостей половину времени, затраченного на дорогу, он получает возможность узнать время прихода домой и перевести соответствующим образом стрелки своих часов.

Задача №66

11. Задача о медведе. Эта задача обладает любопытной особенностью: многие слышали ее и знают ответ, но рассуждения, при которых они пытаются обосновать его, совершенно неудовлетворительны. Поэтому, даже если вы считаете, что знаете ответ задачи, проверьте себя, заглянув в решение.

Охотник находится в 100 м к югу от медведя, проходит 100 м на восток, поворачивается лицом к северу, прицеливается и, выстрелив в направлении на север, убивает медведя. Какого цвета медвежья шкура?

Ответ:

Шкура должна быть белой, так как принадлежит белому медведю, обитающему в Арктике - вблизи Северного полюса. Обычно ответ подкрепляют ссылкой на то, что медведь, о котором говорится в условиях задачи, должен стоять на Северном полюсе. Это лишь одна, но не единственная возможная ситуация. В каком бы направлении ни ступить из Северного полюса, двигаться всегда будешь на юг. Поэтому если медведь находится на Северном полюсе, а охотник - в 100 м к югу от него, то, пройдя 100 м на восток и обернувшись на север, охотник окажется лицом к Северному полюсу. Все это так, но, как я уже говорил, приведенное решение не единственно. Действительно, существует бесконечно много решений. Например, охотник может находиться на параллели длиной 100 м, а медведь - в 100 м к северу от него. Пройдя 100 м на восток, охотник опишет полную окружность вокруг полюса и вернется в исходную точку. Это второе решение задачи. Но охотник может находиться еще ближе к полюсу на параллели длиной 50 м. Пройдя 100 м, он дважды опишет полную окружность вокруг полюса и окажется в исходной точке. Но и это еще не все. Охотник может находиться на параллели длиной в 1/3 от 100 м. Трижды обойдя по параллели вокруг полюса, он также окажется в исходной точке. Поскольку аналогичное решение можно построить при любом положительном целом n, то на Земле существует бесконечно много мест, где могла бы разыграться сценка, описанная в задаче.

Разумеется, во всех этих решениях предполагается, что медведь, находившийся достаточно близко от Северного полюса, непременно должен быть белым медведем. Существует, однако, еще одна возможность, хотя она и весьма маловероятна: некий злонамеренный тип умышленно доставил на Северный полюс бурого медведя, чтобы "насолить" автору задачи.

Задача №67

12. У меня две монеты на общую сумму 15 копеек. Одна из них не пятак. Что это за монеты?

Ответ: Пятак и одна монета достоинством в 10 копеек. Одна монета (десятикопеечная) не пятак.

Задача №68

13. Этот вопрос обращен к тем читателям, которые знают хоть что-нибудь о католицизме. Может ли католик жениться на сестре своей вдовы?

Ответ: Как может покойник жениться на ком-нибудь?

Задача №69

14. Некто живет на двадцать пятом этаже тридцатиэтажного здания. Каждое утро (кроме субботы и воскресенья) он входит в лифт, спускается вниз и отправляется на работу. Вечером, вернувшись домой, он входит в лифт, поднимается на двадцать четвертый этаж, а оттуда - пешком - еще на один этаж.

Почему он выходит из лифта на двадцать четвертом этаже вместо того, чтобы подняться прямо на двадцать пятый этаж?

Ответ: Человек, живущий на двадцать пятом этаже, - лилипут и не может дотянуться до кнопки "25 этаж" на пульте лифта.

Задача №70

15. Задача о железнодорожном движении.

Поезд отправляется из Бостона в Нью-Йорк. Через час другой поезд отправляется из Нью-Йорка в Бостон. Оба поезда едут с одной и той же скоростью. Какой из них в момент встречи будет находиться на меньшем расстоянии от Бостона?

Примечание: размерами (длиной) поездов можно пренебречь.

Ответ: Поезда в момент встречи будут находиться на одинаковом расстоянии от Бостона.

Задача №71

16. Наклон крыши.

Крыша одного дома не симметрична: один скат ее составляет с горизонталью угол 60 градусов, другой - угол 70 градусов. Предположим, что петух откладывает яйцо на гребень крыши. В какую сторону упадет яйцо - в сторону более пологого или крутого ската?

Ответ: Петухи не откладывают яйца

Задача №72

17. Сколько девяток? Вдоль улицы стоят 100 домов. Мастера попросили изготовить номера для всех домов от 1 до 100. Чтобы выполнить заказ, он должен запастись цифрами. Не пользуясь карандашом и бумагой, подсчитайте в уме, сколько девяток потребуется мастеру?

Примечание: 6 и 9 - это разные цифры, т. е. переворачивать их нельзя.

Ответ: Двадцать.

Задача №73

18. Беговая дорожка. Чтобы проползти по беговой дорожке одного стадиона по часовой стрелке, улитке требуется полтора часа. Когда же улитка ползет по той же дорожке против часовой стрелки, то полный круг она совершает за 90 мин. Чем объяснить несовпадение результатов?

Ответ: Несовпадения нет: полтора часа по продолжительности не отличаются от 90 минут.

Задача №74

19. Как вы это объясните?

Некий мистер Смит ехал в машине вместе со своим сыном Артуром. Их машина попала в катастрофу. Отец погиб на месте, а сын в тяжелом состоянии доставлен в ближайшую больницу. Взглянув на пострадавшего, дежурный хирург побледнел и сказал: "Я не могу оперировать его. Ведь это же мой сын Артур!"

Как вы это объясните?

Ответ: Хирург был матерью Артура Смита.

--"Жареные семечки" 01:18, 13 ноября 2008 (UZT)

--Весёлые умницы ID_296 14:07, 13 ноября 2008 (UZT)

Задача №1

ЗАДАЧА ИЗ ПАПИРУСА РАЙНДА.

    Найти число, если известно, что от прибавления к нему 2/3 его и вычитания от полученной суммы ее трети получается число 10.

Решение: по условию задачи составляем уравнение х+2/3 х- 1/3 (х+2/3 х)=10 , ответ х = 9

Задача №2

ЗАДАЧА ДИОФНТА (Из трактата «Арифметика»)

    Найти три числа так, чтобы суммы всех трех и каждых двух были квадратами.

Решение: Пусть сумма всех трех чисел I + II + III = x2 + 2x +1 = ( x + 1 )2,

а  I + II = x2, тогда  III = 2x +1. Пусть теперь II + III = ( x - 1 )2. Тогда получаем, что I =4x, а II = х2 – 4х. Далее I + III = 6x + 1 должно быть квадратом некоторого числа, например 112 = 121. Тогда для определения  х получаем уравнение 6х + 1 = 121, откуда х = 20. Значит: I = 80, II = 320, III = 41.

Задача №3

ЗАДАЧА ИЗ «ГРЕЧЕСКОЙ АНТОЛОГИИ»

 - Хроноса (бог ремени) вестник, скажи, какая часть дня миновала?    
 - Дважды две трети того, что прошло, остается. ( У древних греков день длился 12 часов.)

Решение: по условию задачи составляем уравнение 4/3 х+х=12 , ответ х = 5 1/7 дня

Задача №4

ЗАДАЧА ИЗ БАХШАЛИЙСКОЙ РУКОПИСИ ( найдена в 1881г. Ри раскопках в Бахшали в северо-западной ИНДИИ. Рукопись выполнена на березовой коре и относится к 3 или 4 веку н. э.)

    Из четырех жертвователей второй дал вдвое больше первого, третий – втрое больше второго, четвертый – вчетверо больше третьего, а все вместе дали 132. Сколько дал первый.

Решение: Пусть первый дал 1 часть, второй - 2, третий – 6, четвертый- 24. Сумма пожертвований будет составлять 33. Разделим 132 на 33. Это и будет искомый результат. Ответ 4.

Задача №5

ЗАДАЧА БХАСКАРЫ ( Задача взята из трактата «Венец астрономического учения» индийского математика ХII в. Бхаскары-акария)

    Если некоторое число умножить на 5, от произведения отнять его треть, остаток разделить на 10 и прибавить к этому последовательно 1/3, 1/ 2,1/4 первоначального числа, то получится 68. Как велико число?

Решение: Бхаскара данную задачу решал методом предположения. Предположим, что искомое число равняется 3, тогда, по условию задачи, 3•5=15, одна треть от 15 равна 5. Поскольку15 – 5 = 10, то при делении 10 на 10 получим 1. Если к 1 прибавить 1/3, 1/2, 1/4 от 3, тогда получаем 1+1+3/2+3/4=17/4, что меньше 68 в 16 раз. Следовательно искомое число 3•16=48. Ответ 48.

Задача №6

ЗАДАЧА БХАСКАРЫ

   Некто сказал своему другу: «Дай мне 100 рупий, и я буду вдвое богаче тебя», на что последний ответил: «Если ты мне дашь только 10 рупий, я стану вшестеро богаче тебя». Спрашивается, сколько было у каждого.

Решение: Пусть у первого было 2х - 100 рупий, а у второго х + 100 рупий. Ясно, что первое условие будет выполнено. Имея ввиду второе условие, находим 6 ( 2х – 110 ) = х + 110. Решая, получаем х = 70. Значит у первого было 140 – 100 = 40 рупий, у второго 70 + 100 = 170

Задача №7

ЗАДАЧА АЛ-КАРХИ (Среднеазиатский математик ХI в, автор трактата « Все известное в арифметике»)

    Найдите площадь прямоугольника, основание которого вдвое больше высоты, а площадь численно равна периметру.

Решение: Обозначим ширину прямоугольника через х, тогда длина его будет 2х, площадь 2х2, периметр 6х. Согласно условию задачи 2х2 = 6х, следовательно х = 3, и искомая площадь равна 18 кв. ед.

Задача №8

ЗАДАЧА БЕГА-ЭДДИНА ( Иранский математик автор трактата «Сущность искусства счисления»)

    Разделить число 10 на такие две части, разность которых есть 5.

Решение: Если меньшую часть обозначить через х, то большая будет х+5. Согласно условию задачи, 2х +5 = 10. Откуда х = 21/2. Следовательно меньшая часть 21/2, а большая 71/2.

Задача №9

ЗАДАЧА ИЗ «КУРСА АЛГЕБРЫ» А. Н. СТРАННОЛЮБСКОГО (русский математик-методист 1839 – 1903г.)

    Некто на вопрос о возрасте двух его сыновей отвечал: «Первый мой сын втрое старше второго, а обоим им вместе столько лет, сколько было мне  29 лет тому назад; теперь мне 45 лет». Найти лета обоих сыновей.

Решение: Обозначим лета второго сына через х, тогда х +3х = 45 – 29; решая уравнение получаем ответ х = 4

--"Весёлые умницы" 14:49, 13 ноября 2008 (UZT)

--Bookworm ID 213 16:16, 13 ноября 2008 (UZT)

Задача 76. Задача из трактата «Математика в девяти книгах» (Китай). Имеется бамбук из девяти колен. Объём трёх нижних колен 4 шэна, четыре верхних колен 3 шэна. Спрашивается, каковы объёмы двух средних колен, если объём каждого колена отличается от соседних на равную величину.

Решение:

Для решения задачи составитель трактата выводит правило: «4 шэна, разделённых на 3нижних колена, составляют нижний коэффициент; 3 шэна разделённые на 4 верхних колена, составляют верхний коэффициент. Из большего нижнего коэффициента вычти верхний меньший, остаток есть делимое. Сумму половин 4 колен и 3 колен вычти из 9 колен остаток, является делителем. Объедини делимое и делитель, получишь искомое количество в шэнах, т.е. на столько отличается каждая ступень от соседней. Нижний коэффициент, т.е. 1 с малой половиной шэна, есть объём второго снизу колена». Согласно этому правилу, можно провести несложные вычисления: 1) 4/3-3/4 = 7/12 – разность между «верхним» и «нижним» коэффициентами, что составляет делимое; 2) 9-4/2-3/2 = 11/2 составляет делитель; 3) (7/12):(11/2) = 7/66 = d, т.е. то число, на которое отличается каждая ступень от соседней; 4) тогда второе снизу колено будет составлять 4/3 = 1 1/3 (шэна). Теперь без труда можно найти в шэнах и другие восемь колен.

Задача №77. Задача из трактата «Математика в девяти книгах» (Китай). Имеется 9 слитков золота и 11 слитков серебра, их взвесили, вес как раз совпал. Переложили слиток золота и серебра, золото стало легче на 13 ланов. Спрашивается, какой вес слитка золота и серебра каждого в отдельности.

Решение:

Прежде всего, 1 цзинь = 16 ланам, а 1 лан = 24 чжу. Обозначим теперь вес слитка золота через х, а вес слитка серебра через z; задача сводится к решению системы: 9х = 11z; 13+8x+z = 10z+x. Будем решать эту систему по правилу двух ложных положений. Первое ложное положение x1 = 3 цзиням. Тогда: z1= 9x1/11 = 9·3/11 = 27/11 = 2 5/11 (цзиням). Находим теперь «недостаток в правой строке», обозначив его через у1: у1 = (13/16+8·3+2 5/11)-(10·2 5/11+3) = 27·(47/11·16) – 27·(96 /11·16) = -49/11·16. Второе ложное положение х2 = 2 цзиням. В этом случае z2 = 1 7/11 цзиня и «избыток в левой строке» будет: y2 = (13/16+1 7/16+8·2)–(10·1 7/11+2) = 18·(79/11·16)-18·(64/11·16) = 15/11·16. Далее предполагается, что у1 и у2 вместе с х1 и х2 записаны по китайскому способу:

х2 х1 у2 у1 где левая колонка составляет «левую строку», а правая колонка –«правую строку». Из этой таблицы, согласно правилу, получаем: х = ( 2·(49/11·16)+3·(15/11·16))/ (49/11·16+15/11·16 )= 143/64 = 2 15/64 (цзиня). Следовательно, х = 2 цзиня 3 ланам 18 чжу. Вес слитка серебра определяется очень просто. Для этого делимое 143 надо разделить на произведение делителя 64 и знаменателя 11/9. Тогда получаем: z = x:(11/9) = 143:(11/9·64) = 13·9/64 = 117/64 = 1 53/64 (цзиня). Следовательно, окончательно z = 1 цзиню 13 ланам и 6 чжу.

Задача №78. Задача из трактата «Математика в девяти книгах» (Китай). Рысак и кляча движутся от Чаньяня к княжеству Ци, которое удалено от Чаньяня на 3000 ли. В первый день рысак пробегает 193 ли, каждый следующий день пробегает на 13 ли больше. Кляча в первый день пробегает 97 ли, каждый следующий день пробегает на половину ли меньше. Рысак первым достигает княжества Ци, повернул обратно ив некотором месте встретил клячу. Спрашивается, через сколько дней они встретятся и сколько ли пробежала каждая лошадь.

Решение:

Составитель трактата для решения этой задачи предлагает такое правило: «Предположим, что через 15 дней, тогда недостаток 337 с половиной ли. Предположим, что через 16, тогда избыток равен 140 ли. Избыток и недостаток – это делитель. Объедини делимое и делитель, получишь искомое количество дней. Если разделится не до конца, то сократи на общий делитель и обозначь делитель». За n целых дней рысак пробежит: 193+(193+13)+(193+2·13)+…+[193+(n-1)·1] = 193n+13+2*13+…+(n-1)·13 = 193n+13[1+2+…+(n-1)] = 193n+13·(n(n-1)/2) (ли). За это же число дней кляча пробежит: 97+(97-0.5)+(97-2·0.5)+…+[97-(n-1)·0.5] = 97n-0.5[1+2+…+(n-1)] = 97n-0.5·(n(n-1)/2) (ли). За указанное число дней русак и кляча пробегут вместе. 193n+13·(n(n-1)/2)+97n-0.5·(n(n-1)/2) = 290n+(13-0.5)·(n(n-1)/2) = 290n +6.25(n2-n) (ли). что должно составить 6000 ли. Далее, придерживаясь указанного выше правила, задачу решать методом двух ложных положений. При n = 15 недостаток равен 6000-5662.5 = 337.5 (ли); при n = 16 избыток составляет 6140-6000 = 140 (ли). Обозначая время встречи через х, и предполагая, что на протяжении дня скорости не менялись, получим: х =(15·140+16·337.5)/(140+337.5)=15 135/191 (дня). Теперь не составляет большого труда найти, столько ли пройдут рысак и кляча за 15 135/191 дня.

Задача №79. Задача из трактата «Математика в девяти книгах» (Китай). 5 буйволов и 2 барана стоят 10 ланов золота, 2 буйвола и 5 баранов стоят 8 ланов. Спрашивается, сколько стоят буйвол и баран. Решение: Эта задача в трактате решается правилом «фан-чэн», с которым мы познакомимся дальше. Очевидно, вопрос сводится к системе уравнений: 5х+2у=10

2х+5у=8.

Ответ:34/21 лана стоит буйвол и 20/21 лана стоит баран.

Задача №80. Задача из трактата «Математика в девяти книгах» (Китай). Два снопа урожая А, 3 снопа урожая Б, 4 снопа урожая В превышают по весу дань: вес 2 снопов урожая А превышает дань на вес 1 снопа урожая Б, вес 3 снопов урожая Б – на вес 1 снопа урожая В, вес 4 снопов урожая В – на вес 1 снопа урожая А. Спрашивается , каков вес каждого из снопов урожаев А,Б,В.

Решение : Задача сводится к решению системы: 2х = 1+у

3у = 1+z

4z = 1+x

Её каноническая форма:

2x-y = 1

3y-z = 1

4z-x = 1

Выразим у = 2 х – 1,и подставим во второе уравнение. Получим 6 х = 4 + z. но х = 4 z – 1 . Тогда z = 10/23 , х = 17/23, у = 11/23 Ответ: 17/23, 11/23, 10/23

Задача №81. Задача из трактата «Математика в девяти книгах» (Китай). Продали 2 буйвола, 5 баранов, купили 13 свиней, осталось 1000 цяней. Продали 3 буйвола 3 свиньи, купили 9 баранов, как раз хватило. Продали 6 баранов, 8свиней, купили 5 буйволов, не хватило 600 цяней. Спрашивается, сколько стоят буйвол, баран и свинья.

Решение:

Установи, что 2 буйвола, 5 баранов положительны, 13 свиней отрицательны, остаток цяней положителен. Ещё установи, что 3 буйвола положительны, 9 баранов отрицательны, 3 свиньи положительны. Ещё установи, 5 буйволов отрицательны, 6 баранов положительны, 8 свиней положительны, недостаток цяней отрицателен. Обозначив x, y, z соответственно стоимости буйвола, барана и свиньи, сведём задачу к решению системы:

2x+5y = 13z+1000

3x+3z = 9y

6y+8z = 5x-600,

где 1000 – остаток цяней от продажи 2 буйволов, 5 баранов и покупки 13 свиней; 600 – недостаток цяней от продажи 6 баранов, 8 свиней, покупки 5 буйволов. Решив эту систему уравнений получаем: х= 300, у = 110, z= 30 Ответ: 300 буйволов, 110 барановЮ 30 свиней.

Задача №82. Задача из трактата «Математика в девяти книгах» (Китай). Имеется водоём со стороной в 1 чжан. В центре его растёт камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его. Спрашивается, какова глубина водоёма и какова длина камыша. (1 чжан = 10 чи).

Решение:

Обозначим длину водоёма через 2а, длину камыша через с. Задача заключается в нахождении b и с. Руководствуясь китайским правилом находим формулу для определения искомых величин: b = (a2-(c-b))/2(c-b); c = b+(c-b) = (a2-(c-b))/2(c-b). Исходя из условий задачи применяя правило «гоу-гоу», т.е. теорему Пифагор, получаем систему:

b = c-k

b2 = c2-a2,

где для кратности k обозначена известная нам надводная часть, равная c-b. Решая систему, будем иметь: b = (a2-k2)/2k; и c = (a2+k2)/2k, где k = c-b Прежде всего по правилу «гоу-гоу» имеем: a2 = c2-b2. Далее, получаем: a2 = c2 – b2 = (c-b)2+2b·(c-b) или a2 = (c-b)2+2b(c-b)? откуда b = (a2-(c-b)2)/2(c-b).

Задача №83. Задача из трактата «Математика в девяти книгах» (Китай). Два человека находятся в одном месте. норма ходьбы А есть 7, норма ходьбы Б есть 3. Б идет на восток. А идет 10 бу на юг, а затем идет по космосу направлению на северо-восток до встречи с Б. спрашивается, какой путь прошел каждый из них, А и Б. Решение: Эту задачу древнекитайский математик в трактате рекомендует решать по такому правилу: «7 умножь само на себя, 3 тоже умножь само на себя, сложи и возьми половину. Возьми в качестве нормы ходьбы А по косому направлению. Вычти из 7, умноженного на само себя, норму ходьбы по косому направлению, остаток является нормой ходьбы на юг. 3 умножь на 7, это норма ходьбы Б на восток. 10 бу ходьбы на юг умножь на норму ходьбы А по косому направлению, 10 бу умножь на норму ходьбы Б на восток, каждое есть делимое. Объедини делимое и норму ходьбы на юг, получишь для каждого количество пройденного». Пользуясь этим правилом, задачу можно решить довольно просто: 1) находим сначала норму ходьбы А «по косому направлению»: (49 + 9)/2=29 2) определяем норму ходьбы А на юг: 49-(49+9)/2=20 3) норма ходьбы на восток будет 7 • 3 = 21; 4) находим «делимое»: 10 • 29 и 10 • 21; 5) А прошел «по косому направлению» путь 10•29/20=14,5 бу 6)Б прошел на восток путь 10•21/20=10,5 бу

Обычным путем задача решается так: обозначаем через Х путь, пройденный Б на восток, через У – путь, пройденный а на юг (причем, по условию задачи, у = 10 бу), через Z – путь, пройденный А «по косому направлению», т.е. по гипотенузе полученного прямоугольного треугольника. Тогда, х2 + 10 2= z2 и х/ (z + 10) = 3/7 . Ответ: 14,5 бу и 10,5 бу.

Задача № 84. Задача из трактата «Математика в девяти книгах» (Китай).Имеется дверь, высота которой больше ширины на 6 чи 8 цуней. Наибольшее расстояние между углами (диагональ) 1 чжан. Спрашивается, каковы ширина и высота двери.

Решение: Если обозначить ширину двери через х, а длину через у, далее положить, что у - х = m («избыток»), а диагональ двери d, то задача сводится к рассмотрению системы:

d^2 = x^2 + y^2,

m = y – x.

Для определения х получаем квадратное уравнение: 2х^2 + 2mx + m^2 – d^2 = 0

Задача № 85. Задача из трактата «Математика в девяти книгах» (Китай).Диаметр колодца 5 чи, глубина неизвестна. У верхнего края колодца поставлен шест в 5 чи. Вершина шеста наблюдается на одном уровне с границей воды и стены, а на диаметре откладывается 4 цуня. Спрашивается, какова глубина колодца.

Решение: Надо иметь в виду ,что 1чжан = 10 чи = 100цуням.Для составления нужного правила решения древнекитайские Математики, по всей вероятности, рассматривали два подобных прямоугольных треугольника ∆ABF и ∆FCD, откуда получали AB/BF = x/FC; х = FC · A B/BF; х = AB(BC-BF)/BF. «Объедини делимое и делитель, получишь искомое количество в цунях»

--Bookworm ID 213 16:16, 13 ноября 2008 (UZT)

Копилка знаменитых задач продолжение 6

Содержание

Задачи участников ДООМ

МаГмА ID _205

Совокупность "жареных семечек"ID-224

Участник: Максимум ID_251

Совокупность "жареных семечек"

Просмотры

Личные инструменты

Навигация

Поиск

Инструменты

наши друзья