Уравнения и неравенства с параметрами

Уравнения и неравенства с параметрами
методическое пособие

ВОЕННО-ТЕХНИЧЕСКИЙ КАДЕТСКИЙ КОРПУС

Дисциплина:

«Математика, основы информатики и вычислительной техники»

МЕТОДИЧЕСКОЕ ПОСОБИЕ

для кадет

Тема: Уравнения и неравенства с параметрами.

Преподаватель: Молоткова Л. Ф.

г. Тольятти 2008 г.

Тема: Уравнения и неравенства с параметрами.

Учебные цели: Закрепить и углубить знания основных УЭ по теме.

Учебные вопросы:

1. Линейные уравнения и уравнения, сводящиеся к ним.
2. Линейные неравенства и неравенства, сводящиеся к ним.
3. Некоторые рациональные уравнения и неравенства, сводящиеся к ним.

Предисловие

На вступительных конкурсных экзаменах по математике а вузы часто предлагаются для решения уравнения или неравенства с параметрами. Большинство абитуриентов испытывают затруднения при решении таких задач, ввиду отсутствия у них теоретических и практических навыков их решения. Основной целью данного пособия является привитие и закрепление таких навыков. В методическом пособии изложены основные методы решения уравнений и неравенств с параметрами, входящих во все разделы школьного курса алгебры и начал анализа. По каждой рассматриваемой теме сначала излагается краткая теория и описываются основные методы решения соответствующих задач. Затем разбираются примеры решения наиболее часто предлагаемых на вступительных экзаменах в вузы. Наконец, приводятся задачи для самостоятельного решения.

Линейные уравнения

Часть 1. Линейные уроавнения
Уравнение вида

А х = В, (1)

где А, В – выражения, зависящие от параметров,
х – неизвестное, называется линейным уравнением с параметрами.
Решить уравнение с параметрами – значит для всех значений параметров найти множество корней заданного уравнения.
Линейное уравнение (1) исследуется по следующей схеме:
1) Если А = 0, то имеем уравнение 0*х = В. Тогда, если, кроме того, В 0, то уравнение имеет пустое множество решений (х ), а если В = 0, то уравнение имеет вид 0*х = 0 и удовлетворяется при любом х, т.е. решением уравнения будет множество всех действительных чисел (х R).
2) Если А 0, то уравнение имеет единственное решение .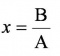
Замечание. Если линейное уравнение или уравнение, сводящееся к линейному, не представлено в виде (1), то сначала его нужно привести к виду (1) (стандартному виду) и только после этого проводить исследование. Если для каких-нибудь значений параметров уравнение не имеет смысла, то для этих значений параметров множество решений уравнения пусто. Кроме этого, уравнение может иметь пустое множество решений и при других значениях параметров.
Скачать задачи и решения

Линейные неравенства и неравенства, сводящиеся к ним

Часть 2. Линейные неравенства и неравенства, сводящиеся к ним
Неравенства А х > В, А х < В, А х  В, А х  В,
где А, В – выражения, зависящие от параметров,
х – неизвестное, называются линейными неравенства-ми с параметрами.
Решить неравенство с параметрами – значит для всех значений параметров найти множество решений заданного неравенства. Неравенство вида А х > В исследуется по следующей схеме:
1) Если А > 0, то .
2) Если А < 0, то .
3) Если А = 0, то неравенство имеет вид 0х >B. При В0 неравенство имеет пустое множество решений; при В<0 решением неравенства будет множество всех действительных чисел R.
Остальные неравенства исследуются аналогично.
Скачать задачи и решения

Некоторые рациональные уравнения и неравенства, сводящиеся к линейным

Часть 3. Некоторые рациональные уравнения и неравенства, сводящиеся к линейным
Скачать задачи и решения

Задачи, в которых надо найти не все возможные решения, а лишь те из них, которые удовлетворяют некоторым дополнительным условиям

Часть 4. Задачи, в которых надо найти не все возможные решения, а лишь те из них, которые удовлетворяют некоторым дополнительным условиям
Скачать задачи и решения

Читать полную версию