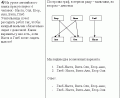
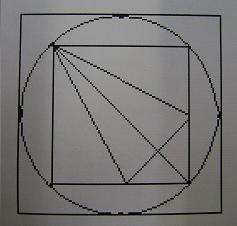
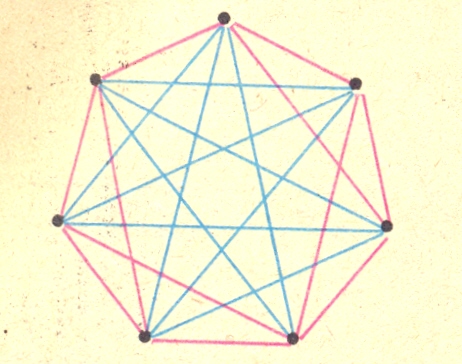
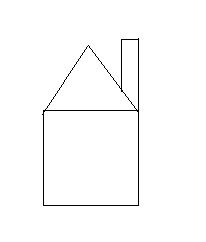
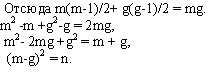Блиц-конкурс ДООМ 2007-2008 (1 цикл)

Надеемся, вам понравилось решать задачи, которые были подготовлены организаторами олимпиады. Но мы думаем, что у каждого из вас есть интересные задачи по теме олимпиады в вашей копилке, и хотим, чтобы вы поделились ими с нами и с соперниками. Поэтому предлагаем вам принять участие в блиц-конкурсе.

Внимание!

• Условие задачи размещается командой на вики – странице Блиц-конкурс ДООМ (в разделе с именем команды) с указанием e-mail команды не позднее 10 декабря.
• Авторы оценивают решения своих задач, присланные соперниками, и результаты оценивания размещают на странице Блиц-конкурс ДООМ (в разделе с именем команды) сразу под условием задачи до 14 декабря.
• Свой вариант решения задачи команда размещает на вики – странице Блиц-конкурс ДООМ (в разделе с именем команды, под результатами оценивания) 13 декабря и 14 декабря 2007 г.

Для этого выполните следующие действия:

1. Нажмите ссылку [править] напротив названия своей команды и в поле визуального редактора впишите название своей команды и текст задач (результаты оценивания, решение задач).
2. Нажмите кнопку Записать страницу.

Задачи, размещенные позже 10 декабря, в конкурсе не участвуют!!!

Команда 001 "Пифагорейцы"

Ваши решения и ответы просим присылать по адресу: school28@edu.tgl.ru

1. В трёх банках находятся: крупа, вермишель и сахар. На банках написано: "Крупа", "Вермишель" и "Крупа или сахар", но содержимое каждой банки не соответствует надписи. Что лежит в банке с надписью "Крупа"?

Команда "Графство "жареных семечек"" решила задачу верно

Команда "Смежные вершины" решила задачу верно

Команда "ГрафОграфы" решила задачу верно

Команда "Новички" решила задачу верно

Команда "ЛОГО" решила задачу верно

Команда "Альтаир" решила задачу верно

Команда "Львы" решила задачу верно

Решение: Так как содержимое каждой банки не соответствует надписи, то после построения графа ясно, что крупа лежит в банке с надписью "Вермишель", вермишель - в банке с надписью "Крупа и сахар", а сахар - в банке с надписью "Крупа".

Ответ: в банке с надписью "Крупа" находится сахар.

2. Джентльмены А, В, С, Д и Е встретились в клубе. Некоторые из них приветствовали друг друга рукопожатиями, причём А и В пожали руки по одному разу, а С, Д и Е - по два. Известно, что А пожал руку Е. Какого рукопожатия наверняка не было?

Команда "Графство "жареных семечек"" решила задачу верно

Команда "Смежные вершины" решила задачу верно, но есть ещё вариант

Команда "ГрафОграфы" решила задачу верно, но есть ещё вариант

Команда "Новички" решила задачу верно, но есть ещё варианты

Команда "ЛОГО" решила задачу верно, но есть ещё варианты

Команда "Альтаир" решила задачу верно, но есть ещё варианты

Команда "Львы" решила задачу верно, но есть ещё варианты

Решение: Если построить граф и соединить джентльменов А и Е, то ясно, что все остальные кроме В могут соединяться по 2 раза исключая соединения с А, т. к. А соединяется только 1 раз. Знаем, что В обменивается рукопожатием только один раз, то это может быть любой кроме А. Значит, рукопожатия А – В не было. По той же причине не было рукопожатия А – С, А – Д, В – Е.

Ответ: А – В, А – С, А – Д, В – Е.

3. У каждого из четырёх ребят живёт какое-то одно любимое животное: кошка, собака, рыбка или канарейка, причём у всех разные. У Миши - животное с пушистой шерстью, у Феди - четвероногое, у Коли - пернатое. Женя и Миша не любят кошек. Инспектор по охране животных записал, что у Феди - собака, у Коли - канарейка, у Жени - рыбка, у Миши - собака, у Феди - кошка. Какая из записей инспектора неверна?

Команда "Графство "жареных семечек"" решила задачу верно

Команда "Смежные вершины" решила задачу верно

Команда "ГрафОграфы" решила задачу неверно

Команда "Новички" решила задачу верно

Команда "ЛОГО" решила задачу верно

Команда "Альтаир" решила задачу верно

Команда "Львы" решила задачу верно

Решение: У Миши - животное с пушистой шерстью, значит кошка или собака. У Феди - четвероногое, значит тоже кошка или собака. У Коли - пернатое, значит канарейка. Так как Женя и Миша не любят кошек, то у них могут быть соответственно рыбка и собака. Это значит, что у Феди кошка. Таким образом, запись о том, что у Феди собака – неверна.

Ответ: у Феди – собака.

Команда 005 "Графство №90"

Ваши решения просим присылать на адрес: ssa@school90.tgl.ru

1. Прощаясь с Иваном-Царевичем, Баба-Яга сказала: "От моей избушки отходят три пути, от каждого из них еще три. Все пути ведут в Кощеево царство. Сколько их - считай сам, но самый короткий путь будет, если следовать моему совету: выбирай не самую левую дорогу, но левее правой". По какому пути Иван-Царевич должен пойти в царство Кощея?

Команда 025 "Смежные вершины" решила задачу верно
Команда 053 решила задачу верно
Команда 011 решила задачу верно
Команда 061 решила задачу верно
Команда 037 решила задачу верно
Команда 062 решила задачу верно
Команда 040 решила задачу верно
Команда 001 решила задачу верно
Команда 010 дала правильный ответ

2. Для озеленения района по плану архитектора нужно посадить аллею зеленых саженцев, чередуя хвойные, лиственные деревья и кустарники. Были предложены три группы растений. В первую группу входят хвойные деревья: ель и сосна; во вторую группу - лиственные деревья: береза, дуб, липа; в третью - кустарники: жасмин, сирень, шиповник. Найдите все варианты озеленения, если известно, что дуб плохо влияет на рост жасмина и сирени, липа - на рост шиповника. Несовместимы: сосна и береза, сосна и липа, ель и дуб, ель и береза.

Команда 025 "Смежные вершины" решила задачу верно
Команда 053 решила задачу не полностью
Команда 011 решила задачу верно
Команда 061 решила задачу верно
Команда 037 решила задачу верно
Команда 062 решила задачу верно
Команда 040 решила задачу верно

3. Сколько трехзначных чисел можно составить из цифр 1, 3, 5 при условии, что цифры в записи повторяться не будут? Перечислите эти числа.

Команда 025 "Смежные вершины" решила задачу верно
Команда 053 решила задачу верно
Команда 011 решила задачу верно
Команда 061 решила задачу верно
Команда 037 решила задачу верно
Команда 062 решила задачу верно
Команда 040 решила задачу верно
Команда 010 дала правильный ответ

4. На уроке английского языка присутствуют 6 человек - Настя, Оля, Егор, Аня, Витя, Глеб. Учительница хочет рассадить ребят так, чтобы каждый мальчик обязательно сидел с девочкой. Какие варианты у нее есть, если Настя и Глеб хотят сидеть вместе?

Команда 025 "Смежные вершины" решила задачу верно
Команда 053 решила задачу не полностью
Команда 011 решила задачу верно
Команда 061 решила задачу верно
Команда 037 решила задачу верно
Команда 062 решила задачу верно
Команда 001 решила задачу верно
Команда 010 дала правильный ответ

5. Ребята сидели на трех лодках и ожидали еще трех своих товарищей - Тараса, Федю и Игната, которые задержались, покупая для всех продукты. Когда опоздавшие подошли к реке, то внимательно посмотрели, как распределились в лодках их друзья. Зная, что им надо сесть в разные лодки, они выразили такие пожелания:
Тарас: "Я хотел бы сесть в первую или во вторую лодку".
Федя: "Мне хочется сесть в первую или в третью лодку".
Игнат: "Я бы сел во вторую или третью лодку".
Определите, сколько существует вариантов решения, и перечислите их.

Команда 025 "Смежные вершины" решила задачу верно
Команда 053 решила задачу не полностью
Команда 011 решила задачу верно
Команда 061 решила задачу верно
Команда 037 решила задачу верно
Команда 062 решила задачу верно
Команда 040 решила задачу верно
Команда 001 решила задачу верно
Команда 010 дала правильный ответ

Правильные ответы:

• 

  ответы и решения к 1 задаче

• 

  ответы и решения ко 2 задаче

• 

  ответы и решения к 3 задаче

• 

  ответы и решения к 4 задаче

• 

  ответы и решения к 5 задаче

Команда 006 "ГрафУм"

Ваши решения просим присылать на адрес: ssa@school90.tgl.ru

1. У Юры два автомобиля, четыре медвежонка и три мяча. Он хочет выбрать из этих игрушек один автомобиль, одного медвежонка и один мяч. Сколько у него есть вариантов выбора?

Команда 025 "Смежные вершины" решила задачу верно
Команда 011 решила задачу верно
Команда 037 дала правильный ответ
Команда 062 дала правильный ответ

Решение:
2×4×3 = 24 варианта выбора.
Ответ: у Юры 24 варианта выбора игрушек.

2. На уроке в танцкласс пришли слон, волк и лев. Партнершами для них были выбраны мышка, белочка и лисичка. Помогите учителю расставить их в пары, если белочка боится, что ее съест волк, а слон - что он раздавит мышку. Сколько вариантов составления пар есть у учителя танцев. Перечислите их.

Команда 025 "Смежные вершины" решила задачу верно
Команда 011 решила задачу верно
Команда 037 решила задачу верно
Команда 062 решила задачу верно

Решение:
Вариант 1. Пусть Белочка танцует со львом. Тогда мышка может танцевать только с волком, значит лисичка танцует только со слоном. Получаем пары: лисичка-слон, белочка-лев, мышка-волк.
Вариант 2. Пусть белочка танцует со слоном. Тогда лисичка может танцевать со львом, остаётся, что мышка танцует с волком. Получаем пары: белочка- слон, лисичка-лев, мышка-волк.
Вариант 3. пусть белочка танцует со слоном, тогда мышка может танцевать только со львом, значит лисичка танцует с волком. Получаем пары: белочка-слон, лисичка-волк, мышка-лев.
Ответ:
Вариант 1: лисичка-слон, белочка-лев, мышка-волк.
Вариант 2: белочка-слон, лисичка-лев, мышка-волк.
Вариант 3: белочка-слон, лисичка-волк, мышка-лев.

3. В связи с плохой погодой задерживаются три рейса самолетов - в Читу, Минск, Петрозаводск. Командиры самолетов высказали пожелания, чтобы рейс в Читу был первым или вторым, в Минск - вторым или третьим, в Петрозаводск - первым или третьим. Можно ли удовлетворить пожелания летчиков? Если да, то перечислите возможные варианты вылетов.

Команда 025 "Смежные вершины" решила задачу верно
Команда 011 решила задачу верно
Команда 037 решила задачу верно
Команда 062 решила задачу верно

Решение:
Чита: 1 и 2 рейс.
Минск: 2 и 3 рейс.
Петрозаводск: 1 и 3 рейс.
Ответ: возможны 2 варианта вылетов:
Чита – 1 рейс, Петрозаводск – 3 рейс, Минск – 2 рейс;
Чита – 2 рейс, Минск – 3 рейс, Петрозаводск – 1 рейс.

4. Даны четыре игрушки - кубик, машинка, рыбка и лодка. Сколькими способами их можно поставить друг рядом с другом?

Команда 025 "Смежные вершины" решила задачу верно
Команда 011 решила задачу верно
Команда 037 дала правильный ответ
Команда 062 решила задачу верно

Решение:
4 = 1×2×3×4 = 24 способа. Ответ: игрушки можно поставить друг рядом с другом 24 способами.

5. На планету Земля из космоса пришли таинственные радиосигналы с предупреждением о начале сжатия нашей галактики Млечный Путь, с последующим превращением ее в "черную дыру", мощным взрывом и вспышкой сверхновой звезды.
После расшифровки удалось установить, что сигналы были посланы из созвездия Персея, туманности Андромеды и Магеллановых облаков.
В эти невиданные ранее для землян дали снаряжаются три экспедиции на новейших космических кораблях с аннигиляционными двигателями: Пегасе (летит в туманность Андромеды), Пожиратели пространства (летит в созвездие Персея), и Голубом пламене (летит к Магеллановым облакам). Формируются три экипажа этих кораблей из состава космонавтов - исследователей, астронавтов и навигаторов.
В каждый экипаж должны войти два юноши и две девушки. Отбор идет среди юношей - Юрия, Криса, Стива, Леонида, Эли, Ивана; девушек: Ольги, Джой, Наталии, Татьяны, Ребекки, Шарон.
Юрий, Леонид, Иван, Ольга, Татьяна - русские, остальные - американцы.
Найдите варианты формирования экипажей, если известно, что:
1) в каждом космическом корабле должны быть двое русских и двое американцев;
2) Леонид мечтает лететь вместе с Ольгой, Эли - с Джой, Иван - с Ребеккой, Крис - с Наталией;
3) Леонид и Эли готовятся к полету в созвездие Персея, Иван - в туманность Андромеды.

Команда 025 "Смежные вершины" решила задачу верно
Команда 011 решила задачу верно
Команда 037 решила задачу верно

Решение:
3 варианта:
1) Иван, Ребекка, Юрий, Шарон летят к Туманности Андромеды; Леонид, Ольга, Эли, Джой – в созвездие Персея; Стив, Татьяна, Крис, Наталия – к Магеллановым облакам.
2) Иван, Ребекка, Стив, Татьяна летят к Туманности Андромеды; Леонид, Ольга, Эли, Джой – в созвездие Персея; Юрий, Шарон, Крис, Наталия – к Магеллановым облакам.
3) Иван, Ребекка, Крис, Наталия летят к Туманности Андромеды; Леонид, Ольга, Эли, Джой – в созвездие Персея; Юрий, Шарон, Стив, Татьяна - к Магеллановым облакам.

---

Почему нет оценки решений задач от команды Команды 053 "ЛОГО" --Янина Ирина Владимировна 22:58, 13 декабря 2007 (UZT)

Нет оценки решений задач от команды Команды 061 "Графство "жареных семечек"" --Графство "жареных семечек" 061 08:52, 17 декабря 2007 (UZT)

Команда 008 "Лидер"

Ваши решения просим высылать на адрес: school45@pochtamt.ru

1. Можно ли начертить граф не отрывая карандаша от бумаги?

Команда 025 "Смежные вершины" решила задачу правильно

Команда 061 решила задачу правильно

Команда 011 решила задачу правильно

Команда 010 решила задачу не правильно

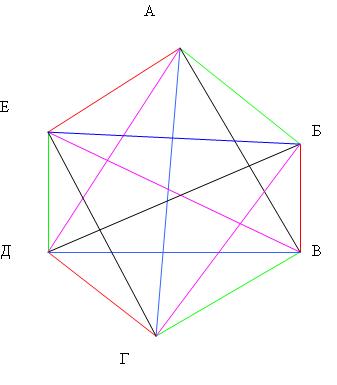
2. Каждая вершина правильного шестиугольника соединятся с каждой из остальных вершин красным или синим отрезком. Докажите, что всегда найдется треугольник со сторонами одного цвета.

Команда 025 "Смежные вершины" решила задачу правильно

Команда 061 решила задачу правильно

Команда 011 решила задачу не правильно

3. В нашей школе проводится турнир по мини-футболу среди мужских и женских команд. От нашего класса составлены: женская команда из пяти девочек и мужская - из пяти мальчиков. В них должны быть по одному вратарю, защитнику, полузащитнику и два нападающих. На эти места есть кандидаты: вратарем хотят быть Коля, Дима, Вася, Аня и Настя. Защитниками – Дима, Витя, Аня и Даша. Полузащитниками – Коля, Сергей, Ира и Даша. Нападающими – Сергей, Витя, Вася, Ира, Настя и Таня. Смогут ли они получить места в командах по своему желанию, если первая тренировка показала, что Вася не может быть нападающим, а Сергей – полузащитником. Таня может быть только нападающим, а Аня только вратарем?

Команда 025 "Смежные вершины" решила задачу правильно

Команда 061 решила задачу правильно

Команда 011 решила задачу правильно

Команда 010 дала ответ верный, но не указала решения

4. В купе едут 6 пассажиров, живущих в разных городах: Москве, Ленинграде, Туле, Киеве, Риге и Одессе. Фамилии их – Агеев, Боков, Власов, Громов, Дубов и Елисеев. Известно, что:

 Агеев и москвич – врачи.

 Дубов и ленинградец – учителя.

 Власов и туляк – инженеры.

 Боков и Елисеев – участники Отечественной войны, а туляк в армии никогда не служил.

 Рижанин старше Агеева, а одессит старше Власова.

 Боков и москвич сошли в Киеве, А Власов и рижанин должны были сойти в Виннице.

Определить фамилию, профессию и место жительства каждого из пассажиров.

Команда 025 "Смежные вершины" решила задачу правильно

Команда 061 решила задачу правильно

Команда 011 решила задачу не правильно

---

Правильные ответы:

1.Ответ: Да, можно, т.к. граф содержит только две нечетные вершины А (степень 5) и В (степень 7). Начать чертить надо с вершины А или В.

2.Ответ: Из первой вершины выходит пять ребер. Из них хотя бы три одного цвета. Рассмотрим эти ребра. Они имеют общую вершину, а концы этих ребер являются вершинами треугольника АВС, стороны которого так же ребра данного графа. Если стороны АВС одного цвета, все доказано; если разного, то хотя бы одна из сторон обязательно окрашена тем же цветом что и три ребра вершины 1, а значит, образует с двумя первоначальными ребрами одноцветный треугольник.

3.Ответ: Составим следующую таблицу:

Профессия Фамилия

Москвич врач А Б В Г Д Е

Ленинградец учитель А Б В Г Д Е

Туляк инженер А Б В Г Д Е

Киевлянин А Б В Г Д Е

Рижанин А Б В Г Д Е

Одессит А Б В Г Д Е

Определим профессии пассажиров способом исключения; будем по условиям задачи последовательно в горизонталях исключать отдельные фамилии (первые буквы их). Так, условия (1) и (6) позволяют зачеркнуть у москвича А и Б, у ленинградца по (2) – Д, по (3) и (4) у туляка В, Б и Е, по (5) и (6) у рижанина – А и В, у одессита по (5) – В. По (1) А – врач: зачеркиваем А у инженера и учителя; аналогично зачеркиваем Д у врача и инженера и В у врача и учителя. Рассматривая вертикаль В, делаем 2 вывода: 1) фамилия киевлянина – Власов и по (3) он инженер; 2) в горизонтали киевлянина можно зачеркнуть все буквы, кроме В. Теперь в вертикали А окажутся зачеркнутыми все А, кроме клетки одессита: 1) одессит – Агеев и по (1) он врач; 2) в горизонтали одессита можно зачеркнуть все буквы, кроме А. Буква Д окажется зачеркнутой 5 раз: рижанин – Дубов – учитель, и в его горизонтали все буквы, кроме Д, зачеркиваются. Тогда Б остается лишь один раз: Боков – ленинградец, учитель. Продолжая, получим: Елисеев – москвич, врач; туляк – Громов, инженер. Ответ: Елисеев - москвич и врач; Боков – ленинградец и учитель; Громов – туляк и инженер; Власов – киевлянин и инженер; Дубов – рижанин и учитель; Агеев – одессит и врач.

4.Ответ: Составим графы (по условиям задачи).

вратарь – Аня и Вася защитник – Даша и Дима полузащитник – Ира и Коля нападающие – Настя, Таня и Сергей, Витя

---

Команда 010 "Лемниската"

Головоломка. Нарисуйте полный граф с семью вершинами. Можно ли раскрасить этот граф двумя цветами (красным и синим) так, чтобы не получилось синих треугольников и получилось не более четырех красных треугольников?

Решение:

Команда 025 "Смежные вершины" задачу решили верно

Команда 011 "ГрафОграфы"

1. Требуется подключить к сети люстру с 15 лампочками так, чтобы можно было зажигать любое количество лампочек (в том числе, и не одной). Можно ли это сделать, если разрешить использовать только четыре выключателя?

Ответ: Каждый из включателей имеет два состояния включен или выключен (0 или1). Значит, занумеровав выключатели, мы имеем 16=24 всевозможных комбинаций их состояний (количество различных чисел в двоичной системе счисления, имеющих не более четырех знаков). Количество состояний люстры также равно 16, то есть мы сможем установить взаимно-однозначное соответствие между множеством состояний выключателей и множеством состояний люстры. Т.е. можно.

Команда 025 "Смежные вершины" решили правильно

Команда 061 Графство"жареных семечек" решили правильно

Команда 005 "Графство №90" решили правильно

Команда 006 "ГрафУм" решили правильно

Команда 040 "Львы" решили задачу правильно.

2. На некотором острове расположено 15 государств. Для каждого из них хотя бы одно соседнее государство – дружественное. Докажите, что найдется государство, у которого четное количество дружественных соседей. (два государства называют соседними, если у них имеется целый кусок общей границы)

Ответ: Предположим, что у каждого государства нечетное количество дружественных соседей, тогда, сложив 15 нечетных чисел, получим нечетное число. С другой стороны, если государство А дружественно государству В, то и в дружественно А (отношение «дружбы» между государствами обладает свойством симметричности). Следовательно, найденная нами сумма должна быть четной. Из полученного противоречия следует, что наше предположение неверно и хотя бы у одного государства четное количество дружественных соседей, что и требовалось доказать.

Команда 025 "Смежные вершины" решили правильно

Команда 061 Графство"жареных семечек" решили правильно

Команда 005 "Графство №90" решили правильно

Команда 006 "ГрафУм" решили правильно

Команда 062 "Альтаир" решили правильно

3. В городе отличников от каждой площади отходит ровно пять улиц, причем каждая улица соединяет ровно две площади. Докажите, что количество площадей в этом городе четно, а количество улиц кратно пяти.

Ответ: Пусть количество площадей – n, а количество улиц – m, тогда количество улиц, соединяющих все площади, должно быть равно 5n/2. Получим уравнение в натуральных числах: 5n = 2m. Так как НОД (2;5)=1, n кратно двум, а m кратно пяти, что и требовалось доказать.

Команда 025 "Смежные вершины" решили правильно

Команда 061 Графство"жареных семечек" решили правильно

Команда 005 "Графство №90" решили правильно

Команда 006 "ГрафУм" решили правильно

Команда 062 "Альтаир" решили правильно

Команда 040 "Львы" решили задачу правильно

Команда 053 решили задачу правильно

4. В школьной олимпиаде по математике участвовали 100 человек, по физике - 50 человек, по информатике - 48 человек. Когда каждого из учеников спросили, в скольких олимпиадах он участвовал, ответ «по крайней мере в двух» дали в два раза меньше человек, чем ответ «не менее чем в одной», а ответ «в трех» - втрое меньше человек, чем ответ «не менее чем в одной». Сколько всего учеников приняло участие в этих олимпиадах?

Ответ: Пусть N - общее количество участников. Тогда, по крайней мере, в двух олимпиадах участвовало N/2 человек, а в трех - N/3. Сложив числа, данные в условии получим: N=(100+50+48)- N/2- N/3, решением которого является N=108 человек.

Команда 025 "Смежные вершины" решили правильно

Команда 061 Графство"жареных семечек" решили правильно

Команда 005 "Графство №90" решили правильно

Команда 006 "ГрафУм" решили правильно

Команда 053 решили задачу правильно

Наш адрес:Glotovskool@mail.ru

Команда 012 "Смелость"

Студенты Сергей, Александр, Игорь, Эдуард и Юрий, а также студентки Елена, Маша, Катерина, Вера и Люба решили идти в байдарочный поход на байдарках-двойках. Выяснилось, что несколько из них, а именно Катерина, Маша, Люба, Александр и Сергей, плавают хуже остальных, поэтому их не следует сажать в одну байдарку. Катя терпеть не может Эдуарда и Юрия, а Юрий и Игорь постоянно ссорятся с Любой. Распределите студентов по байдаркам так, чтобы в каждой байдарке оказались юноша с девушкой.

адрес локального координатора команды iaran@mail.ru

Команда 025 "Смежные вершины" решила задачу правильно

Команда 061 "Графство жареных семечек" решила задачу правильно

Команда 062 решила задачу не полностью

Команда 040 указала не все ответы

Команда 013 "Товарищество"

Можно ли нарисовать данную картинку, не отводя карандаш от бумаги?

Коианда 025 решила задачу верно

Команда 061 решила задачу верно

Команда 001 решила задачу верно

Команда 040 решила задачу верно

адрес локального координатора iaran@mail.ru

Команда 014 "Триада"

Расстояние между деревнями Анохино и Барыгино 4 км, между Барыгино и Колобово 5 км, между Дворищи и Емелино 4 км, между Емелино и Барыгино 5 км. Начальство решило сэкономить на постройке дорог и построить дорогу минимальной длины, так чтобы между любыми деревнями хоть как-то можно было проехать. Где проложили дорогу и какой длины она оказалась?

адрес локального координатора команды iaran@mail.ru

Команда 018 " Секрет"

1. Маша, Лида, Женя и Катя умеют играть на разных инструментах (вилончели, рояле, гитаре и скрипке), но каждая только на одном. Они же владеют разными иностранными языками (английским, французким, немецким и испанским), но каждая только одним. Известно, что: 1. девушка которая играет на гитаре, говорит по-испански; 2. Лида не играет ни на скрипке, ни на виолончели и не знает английского языка; 3. Маша не играет ни на скрипке, ни на велончели и не знает английского языка; 4. девушка, которая говорит по-немецки, не играет на виолончели; 5. Женя знает французкий язык, но не играет на скрипке. Кто на каком инструменте играет и какой иностранный язык знает?

Команда 005 "Графство №90" решила задачу верно

Команда 006 "ГрафУм" решила задачу верно

Команда 025 "Смежные вершины" решила задачу верно

Команда 061 "Графство"жареных семечек"" решила задачу верно

Ответ:Возможны два варианта решения задачи.1.Катя играет на скрипке и говорит на английском языке. Женя на виолончели и говорит на французском языке. Лида играет на рояле и говорит на немецком, Маша играет на гитаре и говорит на испанском. 2. Катя играет на скрипке и говорит на английском языке. Женя на виолончели и говорит на французском языке. Лида играет на гитаре и говорит на испанском. Маша играет на рояле и говорит на немецком.

2.В первенстве класса по теннису 6 участников: Андрей, Борис, Виктор, Галина, Дмитрий и Елена. Первенство проводилось по круговой системе: каждый из участников играет с каждым из остальных один раз. Некоторые игры уже проведены: Андрей сыграл с Борисом, Галиной и Еленой, Борис с Галиной, Виктор с Галиной, Дмитрием и Еленой. Сколько пар проведено и сколько ещё осталось?

Команда 005 "Графство №90" решила задачу неверно

Команда 006 "ГрафУм" решила задачу неверно

Команда 025 "Смежные вершины" решила задачу неверно

Команда 061 "Графство"жареных семечек"" решила задачу верно

Решение: Игры можно представить в виде полного графа.Вершины (6)-участники, а ребра -партии. Известно,что в полном графе n*(n-1)/2=r,6*5/2=15 - число всех партий.Но уже проведены: Андрей сыграл с Борисом, Галиной и Еленой, Борис с Галиной, Виктор с Галиной, Дмитрием и Еленой, (проведено 7 партий), значит, осталось сыграть 15-7=8. Ответ: сыграно 7 партий, осталось - 8 партий.

3. В государстве система авиалиний устроена таким образом, что любой город соединён авиалиниями не более чем с тремя другими и из любого города в любой другой можно проехать, сделав не более одной пересадки. Какое максимальное число городов может быть в этом государстве?

Команда 005 "Графство №90" решила задачу неверно

Команда 006 "ГрафУм" решила задачу неверно

Команда 025 "Смежные вершины" решила задачу верно

Команда 061 "Графство"жареных семечек"" решила задачу верно

Решение: Пусть существует некоторый город А. Из него можно добраться не более, чем до трёх городов, а из каждого из них ещё не более чем до двух (не считая А)Тогда всего городов не более 1+3+6=10. Значит, всего городов не более 10.

4. В семье четверо детей, им 5, 8, 13 и 15 лет, а зовут их Таня, Юра, Света и Лена. Одна девочка ходит в детский сад, Таня старше Юры, а сумма лет Тани и Светы делится на три. Сколько лет Лене?

Команда 005 "Графство №90" решила задачу верно

Команда 006 "ГрафУм" решила задачу верно

Команда 025 "Смежные вершины" решила задачу верно

Команда 061 "Графство"жареных семечек"" решила задачу верно

Команда 062 "Альтаир" решила задачу верно

Решение: Юре не может быть 5 лет- он не девочка, Таня не может быть 5 и 8 лет – она старше Юры, Тане не может быть 15, т.к. Т+С кратно 3, а ни одна из сумм- 15+5, 15+8, 15+13 – не делится на 3. Значит, Тане- 13 лет. В ходе рассуждений, получим следующие результаты: Юре -8 лет, Тане -13 лет, Свете-5 лет, а Лене -15 лет.

Команда 019 "Новички"

Ответы просим высылать на адрес: school45@pochta.ru

Дополнительные тренировочные задачи международной математической игры «Кенгуру».

Задача 1. У Саши есть 4 карточки с цифрами 1,2,3 и 4.Он составляет из них трехзначные числа. Сколько различных чисел, делящихся на 6, он может получить? (А) 6 (В) 4 (С) 2 (D) 8 (E) 10

---

Команда 025 "Смежные вершины" решила задачу верно

Команда 061 решила задачу верно

Команда 062 "Альтаир" не решила задачу

Команда 040 "Львы" решила задачу верно

Задача 2. Тигра пришел на день рождения Крошки Ру на 5 минут раньше, чем ослик Иа-Иа, но на 3 минуты позже, чем Винни-Пух. Когда все угощение было съедено, гости стали расходиться. Первым ушел Вини-Пух: он ушел на 2 минуты раньше, чем Иа-Иа, и на 5 минут раньше, чем Тигра. На сколько минут Тигра был дольше в гостях, чем Иа-Иа? (А) 2 (В) 4 (С) 6 (D) 8 (Е) ИА-ИА был в гостях дольше, чем Тигра.

---

Команда 025 "Смежные вершины" решила задачу не верно

Команда 061 решила задачу верно

Команда 062 "Альтаир" не решила задачу

Команда 040 "Львы" не решила задачу

Задача 3. Сколько путей, идущих по стрелкам, ведут из А в D? (А) 13 (В) 33 (С) 42 (D) 26 (E) 40

---

Команда 025 "Смежные вершины" решила задачу верно

Команда 061 решила задачу верно

Команда 062 "Альтаир" не решила задачу

Команда 040 "Львы" решила задачу верно

Задача 4. Когда идет дождь, кошка сидит в комнате или в подвале. Когда кошка в комнате, мышка сидит в норке, а сыр лежит в холодильнике. Если сыр на столе, а кошка - в подвале, то мышка – в комнате. Сейчас идет дождь, а сыр лежит на столе. Тогда обязательно (А) кошка в комнате; (В) мышка в норке; (С) кошка в комнате или мышка в норке; (D) кошка в подвале, а мышка в комнате; (E) такая ситуация не возможна.

---

Команда 025 "Смежные вершины" решила задачу верно

Команда 061 решила задачу верно

Команда 062 "Альтаир" решила задачу верно

Команда 040 "Львы" решила задачу верно

Задача 5. Старый гном разложил свои сокровища в 3 разноцветных сундука, стоящих у стены: в один – драгоценные камни, в другой - золотые монеты, а в третий – магические книги. Он помнит, что - красный сундук, правее, чем драгоценные камни; - магические книги правее, чем красный сундук. В каком сундуке лежат магические книги, если зеленый сундук стоит левее, чем синий? (А) в синем; (В) в зеленом; (С) в красном; (Д) нельзя определить; (Е) гном что-то запомнил неверно.

---

Команда 025 "Смежные вершины" решила задачу верно

Команда 061 решила задачу верно

Команда 062 "Альтаир" решила задачу верно

Команда 040 "Львы" решила задачу верно

Задача 6. Во дворе бегают 14 кошек и котят. Каждая кошка-мама вывела на прогулку не меньше двух своих котят. Каким может быть наибольшее количество кошек – мам. (А) 18; (В) 4; (С) 5; (Д) 6; (Е) 7.

---

Команда 025 "Смежные вершины" решила задачу верно

Команда 061 решила задачу верно

Команда 062 "Альтаир" решила задачу верно

Команда 040 "Львы" решила задачу верно

---

Правильные ответы

Задача 1. Для того, чтобы число делилось на 6, оно должно делиться и на 2 и на 3, т.е. оно должно оканчиваться на четную цифру, а сумма его цифр должна делиться на 3. Следующие варианты легко изобразить с помощью графов: а) последняя цифра – 2, тогда остальные две 3 и 4 (сумма цифр - 9), или 1 и 3 (сумма цифр – 6), т.к. первые две цифры можно ставить в любом порядке, то получаем 4 числа. б) последняя цифра – 4, тогда две остальные -2 и 3(сумма -9), получим еще два числа. Ответ: 6(А)

Задача 2. Тигра был в гостях на 5 + (5 – 2) = 8 минут дольше, чем Иа-Иа. Ответ: на 8 минут (D)

Задача 3. Путь из А в Д делится на три типа: А – В – Д , А – С – Д , А – С – В – Д. Подсчитаем количество путей каждого типа. а) Из А в В можно попасть тремя способами, из В в Д можно попасть четырьмя способами, таким образом всего 3 * 4 = 12 маршрутов. б) Для второго типа, рассуждаем как в предыдущем случае. Получаем 3 * 3 = 9 маршрутов. в) Для третьего типа получаем 3 * 1 * 4 = 12. Итого 12 + 9 + 9 +12 = 42 маршрута. Ответ: 42 маршрута (С).

Задача 4. Сейчас идет дождь, поэтому кошка либо в комнате, либо в подвале. Если бы кошка была в комнате, то сыр лежал бы в холодильнике, а он по условию лежит на столе. Значит, кошка сидит в подвале. Итак, сыр – на столе, а кошка – в подвале. Мышка – в комнате. Ответ: (Д)

Задача 5. Первое условие сообщает, что красный сундук - не самый левый, а второе, что он не самый правый. Значит он стоит в середине. Т.к. зеленый сундук левее синего, то сундуки расположены так З – К – С. Значит магические книги(которые правее красного сундука) лежат в синем сундуке. Ответ: (А)

Задача 6. Согласно условию, каждая кошачья «семья» состоит хотя бы из трех животных. Значит семей не больше четырех. Но тогда и кошек-мам не больше четырех. Остается заметить, что если две кошки ведут по три котенка, еще две – по два котенка, то во дворе окажется четыре кошачьих семьи – всего 14 кошек и котят. Ответ: (В)

---

Команда 020 "Искатели приключений"

Ответы просим высылать на наш адрес pascal_90@mail.ru

1.Встретились трое подруг: Белова, Краснова и Чернова. На одной из них было надето черное платье, на другой - красное, а на третьей - белое. Девочка в белом платье говорит Черновой: "Нам надо поменяться платьями, а то цвет наших платьев не соответствует фамилиям". Кто в какое платье был одет?

2. Несколько мальчиков встретились на вокзале, чтобы поехать за город в лес. При встрече все они поздоровались друг с другом за руку. Сколько мальчиков поехало за город, если всего было 10 рукопожатий?

3. Я задумал число. Если к нему прибавить 24, потом полученную сумму умножить на 9, затем из произведения вычесть 76 и, наконец, полученную разность разделить на 19, то получится число 23. Найдите задуманное число.

4. В бутылке, стакане, кувшине и банке находятся молоко, лимонад, квас и вода. Известно, что вода и молоко не в бутылке, сосуд с лимонадом стоит между кувшином и сосудом с квасом, в банке не лимонад и не вода. Стакан стоит около банки и сосуда с молоком. Куда налита каждая жидкость.

Нет оценки решений задач от команды Команды 061 "Графство "жареных семечек" --Графство "жареных семечек" 061 08:54, 17 декабря 2007 (UZT)"

Мы тоже посылали вам свои решения, ребята. --Смежные вершины 025 06:32, 18 декабря 2007 (UZT)

Команда 025 "Смежные вершины"

Решения просим высылать по адресу:

s21ner@neru.sakha.ru

Задача №1

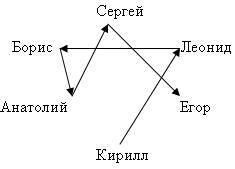
В классе учатся 6 мальчиков: Сергей, Борис, Леонид, Анатолий, Егор и Кирилл. Известно, что Борис ниже Анатолия, а Леонид выше Кирилла, Сергей ниже Егора, Леонид ниже Бориса, Сергей выше Анатолия. Перечислить ребят в в порядке возрастания роста (изобразить граф, с помощью которого выполнено решение).

Команда 062 "Альтаир" решила задачу верно.

Команда 061 "Графство "Жареных семечек" решила задачу верно

Команда 008 "Лидер" решила задачу верно.

Команда 040 "Львы" решила задачу верно.

Команда 040 "Львы" решила задачу верно.(решение отправлено 13.12.07)

Решение:

задача очень легко решается графически, если между вершинами строить ориентированные ребра (например, от более низкого к более высокому), тогда, изобразив все условия задачи в виде стрелок, нужно найти вершину из которой ребро только выходит (самый низкий ученик) и от нее по стрелкам обойти весь граф.

Ответ: Кирилл, Леонид, Борис, Анатолий, Сергей, Егор

Задача №2

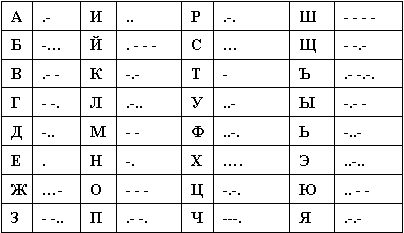
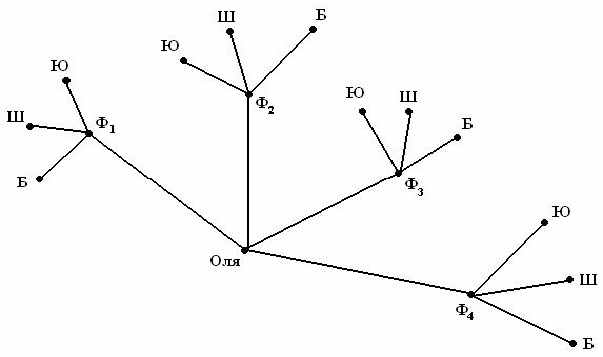
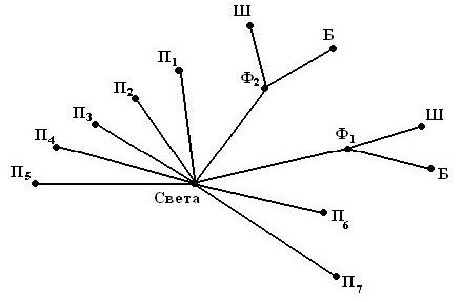
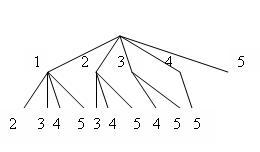
На занятиях в радиокружке Вася получил сообщение от товарища, но так увлекся, что записывая сигналы азбуки Морзе, не поставил разделителей между буквами, вот что у него получилось: 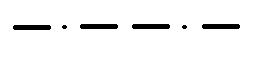Помогите Васе расшифровать послание. Сколько вариантов расшифровки возможно в данном случае? Может быть вы догадаетесь, какое слово было передано Васе.

Команда 061 "Графство "Жареных семечек" решила задачу верно

Команда 008 "Лидер" решила задачу верно.

Команда 040 "Львы" решила задачу верно.

Команда 053 "ЛОГО" решила задачу верно.(решение отправлено 13.12.07)

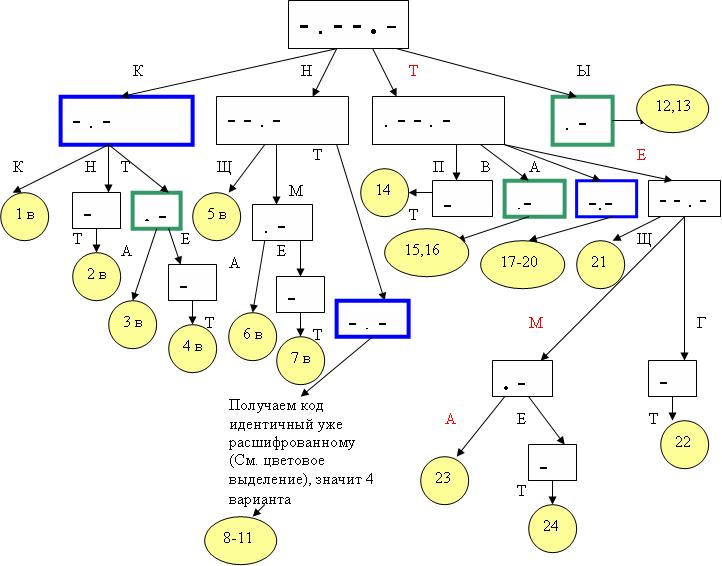
Решение: строим дерево. В корне – послание, анализируем начало послания, выделяем по таблице азбуки Морзе возможные буквы

Как видим из графа, получилось 24 варианта расшифровки, за правильный можно принять вариант 23, где получается осмысленное слово ТЕМА, а не просто набор букв.

Задача №3

Каждые две из шести ЭВМ соединены своим проводом. Укажите, как раскрасить каждый из этих проводов в один из пяти цветов, чтобы из каждой ЭВМ выходило пять проводов разных цветов. Можно ли найти решение для 5-ти ЭВМ? Почему?

Команда 061 "Графство "Жареных семечек" решила задачу верно

Команда 062 "Альтаир" решила задачу верно.

Команда 008 "Лидер" решила задачу неверно.

Команда 053 "ЛОГО" решила задачу верно.(решение отправлено 13.12.07)

Решение:

решение изображено на рисунке. Как мы видим, для решения задачи нужно выделить 5 дополнений к полному графу, который описывает соединение ЭВМ. Эти дополнения должны соответствовать следующим условиям: 1. Отражать все вершины графа. 2. Каждая вершина должна соединяться только с одной другой. 3. Из каждой вершины должно выходить ребро 4. Ребра не должны повторяться в других дополнениях к графу. Понятно, что если вершин будет 5 (т.е нечетное число), то мы не сможем соединить их в дополнении к графу попарно так, чтобы из каждой вершины выходило только одно ребро, значит при нечетном количестве вершин такая раскраска проводов невозможна.

Задача №4

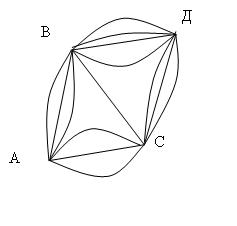
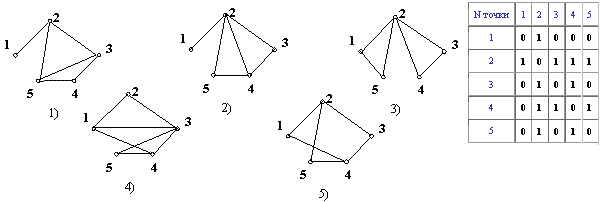
На плоскости заданы 5 точек, их соединения описаны в виде таблицы. Какому графу соответствует таблица?

Команда 062 "Альтаир" решила задачу верно.

Команда 061 "Графство "Жареных семечек" решила задачу верно

Команда 008 "Лидер" решила задачу верно.

Команда 040 "Львы" решила задачу верно.

Команда 053 "ЛОГО" решила задачу верно.(решение отправлено 13.12.07)

Команда 040 "Львы" решила задачу верно.(решение отправлено 13.12.07)

Ответ: в таблице смежности на пересечении номеров вершин единицей отображается наличие ребра, а 0 его отсутствие, сопоставляя данные таблицы с изображениями графов, определяем, что данная таблица отображает граф под № 2

Задача №5

В вазе лежали конфеты четырех сортов. Каждый ребенок взял две конфеты. И у всех оказались отличающие наборы конфет. Сколько могло быть детей?

Команда 062 "Альтаир" решила задачу неверно.

Команда 061 "Графство "Жареных семечек" решила задачу верно

Команда 008 "Лидер" решила задачу верно.

Команда 040 "Львы" решила задачу верно.

Команда 053 "ЛОГО" решила задачу верно., хотя интерпретировала "набор" конфет не так как мы,т.е. как сочетание и двух одинаковых конфет, но это не принципиально(решение отправлено 13.12.07)

Решение: построим граф, у которого вершины – это сорта конфет, а ребро – набор из двух сортов, количество ребер в полном графе определит количество детей – 6.

Примечание:

некоторые команды считали набором и две одинаковые конфеты, тогда получается 10 детей, мы посчитали этот ответ такжк верным.

Желаем всем успехов!!!--Смежные вершины 025 06:53, 2 декабря 2007 (UZT)

---

Ваши косвенные претензии по поводу даты отправления Командой 053 "ЛОГО" ответов на ваши задачи не имеют места быть! Чётких рамок(строго до 13 декабря) указано не было, тем более, наше решение мы вам выслали до того, как вы выложили своё. Привет 8-классникам от 5-клашек!=) --Янина Ирина Владимировна 23:24, 13 декабря 2007 (UZT)

Команда 032 "magic_team"

Cвои ответы просим присылать по адресу: school__41@mail.ru (ВНИМАНИЕ! Между school и 41 ДВА знака подчеркивания)

Задача 1

Четыре брата Юра, Петя, Вова, Коля учатся в 1, 2, 3, 4 классах. Петя-отличник, младшие братья стараются брать с него пример. Вова учится в 4 классе. Юра помогает решать задачи брату. Кто из них, в каком классе учится?

Команда 025 "Смежные вершины" решили правильно

Команда 061 Графство "Жареных семечек" решили правильно

Ответ:

Вова в четвертом классе, Петя в третьем классе, Юра во втором классе, Коля в первом классе.

Задача 2

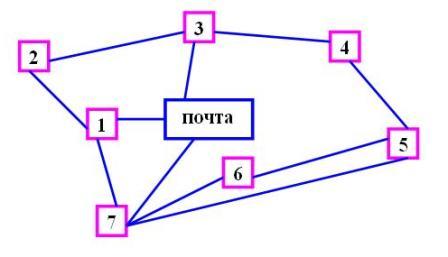
Почтальон Печкин разнёс почту во все дома деревни, после чего зашёл к дяде Фёдору выпить молока. На рисунке показаны все тропинки, которые проходил Печкин, причём, как оказалось, ни по одной из них он не проходил дважды. Каков мог быть маршрут почтальона Печкина? В каком доме живёт дядя Фёдор?

Команда 025 "Смежные вершины" решили правильно

Команда 061 Графство "Жареных семечек" решили не правильно. попрабуйте еще раз. Удачи.

Ответ:

Почта – 1 – 3 –почта – 7 – 1 – 2 – 3 – 4 – 5 – 6 – 7 – 5. Фёдор живёт в доме №5.

Задача 3

Как с помощью двух бидонов 5л и 8л отлить из молочной цистерной 7л молока? Молоко разрешается выливать обратно в цистерну.

Команда 025 "Смежные вершины" решили правильно

Команда 061 Графство "Жареных семечек" решили правильно

Ответ:

1)Налить молоко в пятилитровый бидон и перелить в восьмилитровый.

2)Снова налить молоко в пятилитровый бидон. Тогда в пятилитровом бидоне останется 2л молока.

3)Вылить молоко в цистерну из восьмилитрового бидона.

4)Перелить 2л молока из пятилитрового бидона в восьмилитровый бидон.

5)Налить молоко в пятилитровый бидон и перелить его в восьмилитровый.

В результате в восьмилитровом бидоне получим 2+5=7 (л) молока.

Задача 4

Баба Яга в своей избушке на курьих ножках завела сказочных животных. Все они, кроме двух,- Говорящие Коты. Все, кроме двух,- Мудрые Совы; остальные – Усатые Тараканы. Сколько обитателей в избушке у бабы Яги?

Команда 025 "Смежные вершины" решили правильно

Команда 061 Графство "Жареных семечек" решили правильно

Ответ:

В избушке живут Говорящие Коты, Мудрые Совы и Усатые Тараканы. Из того, что, кроме двух - остальные Говорящие Коты, значит, что Мудрых Сов и Усатых Тараканов вместе двое. Аналогично, из того, что, кроме двух, в избушке – остальные Мудрые Совы; Усатых Тараканов и Говорящих Котов – тоже двое. Эти два условия будут выполняться лишь в двух случаях:

1.Тараканов-2, Сов и Котов-нет или

2.всех - по одному.

Первый случай не подходит, т.к. в условии сказано, что Совы и Коты живут в избушке. Поэтому у Бабы Яги поселились по одному Говорящему Коту, Мудрой Сове и Усатому Таракану, т. е. всего трое.

Задача 5

На волшебной яблоне выросли 3 банана и 4 апельсина. Если сорвать один из плодов – вырастет такой же; если одновременно 2 одинаковых плода – вырастет апельсин, а если одновременно сорвать 2 разных плода – вырастет банан. В каком порядке надо срывать плоды, чтобы на яблоне остался ровно один плод? Можно ли определить какой это будет плод? Можно ли срывать плоды так, чтобы на яблоне ничего не осталось? Желаем удачи в решении задач!!!

Команда 025 "Смежные вершины" решили правильно

Команда 061 Графство "Жареных семечек" решили правильно

Ответ:

Рассмотрим, что будет получаться в каждом из различных случаев. Если сорвать банан, на дереве снова вырастит банан. Если сорвать апельсин, снова вырастит апельсин, т. е. если срывать по одному плоду, ничего не меняется. Сорвем 2 банана, тогда на дереве будет 1 банан и 5 апельсинов, т. е. плодов стало на 1 меньше (бананов уменьшилось, апельсинов увеличилось), больше 2 банана не сорвать. Сорвем 2 апельсина, тогда на дереве останется 3 банана 3 апельсина. Сорвем банан и апельсин, тогда на дереве будет 3 банана и 3 апельсина. Таким образом, срывая по 2 плода, мы получаем, что число плодов уменьшиться на 1, причем число бананов остается все время нечетным. Если срывать 4 раза по банану и апельсину вместе, в итоге останется лишь один банан. Так, чтоб на яблоне не чего не осталось сделать нельзя т. к. на ней всегда остается один плод.

Желаем успехов!

Команда 037 "Интеграл"

Присылайте ваши ответы по адресу Kim9227@yandex.ru

Задача № 1 Даны четыре книги разных авторов - Пушкина, Лермонтова,Толстого и Некрасова.Сколькими способами можно поставить их рядом друг с другом.

Команда 061 "Графство"жареных семечек" решила задачу верно

Команда 025 "Смежные вершины" решила задачу верно

Команда 040 "Львы" решила задачу верно

Команда 053 "ЛОГО" решила задачу верно

Ответ: 2*3*4= 24(способа)

Задача № 2 Сколько различных трехзначных чисел можно записать с помощью 0,1,2 если цифры в числе могут повторяться?

Команда 061 "Графство"жареных семечек" решила задачу верно

Команда 025 "Смежные вершины" решила задачу верно

Команда 053 "ЛОГО" решила задачу верно

Ответ: Цифра 0 может быть либо на месте десятков, либо на месте единиц. 2*3*3=18

Задача № 3 Сколько различных пар элементов(N), отличающихся лишь составом, можно образовать из n имеющихся различных элементов ( n>2)?

Команда 061 "Графство"жареных семечек" решила задачу верно

Команда 025 "Смежные вершины" решила задачу верно

Коамнда 053 "ЛОГО" решила задачу верно

Ответ: N=(n-1)*n/2

Задача № 4 На улице, став в круг, беседуют четыре девочки: Таня,Вера,Оля,Нина. Девочка в зеленом платье( не Таня и не Вера) стоит между девочкой в голубом платье и Ниной. Девочка в белом платье стоит между девочкой в розовом платье и Верой. Какое платье носит каждая из девочек?

Команда 061 "Графство"жареных семечек" решила задачу верно

Команда 025 "Смежные вершины" дала неполный ответ

Команда 053 "ЛОГО" дала непольный ответ

Ответ: 1. Оля в зеленом, Вера в голубом, Таня в белом, Нина в розовом

2. Оля в зеленом, Вера в голубом, Таня в розовом, Нина в белом

Команда 040 "Львы"

Свои ответы просим присылать на адрес: school10_tol@mail.ru

Задача №1

Некоторый граф был начерчен одним росчерком, при этом в вершине А карандаш побывал 5 раз. Определите степень вершины А, если при вычерчивании графа движение карандаша:

a) не с нее начали и не на ней закончили;

b) не с нее начали, но на ней закончили;

c) с нее начали, но не на ней закончили;

d) с нее начали и на ней закончили?

Команда 025 "Смежные вершины" решила задачу верно

Команда 061 "Графство "жареных семечек" решила задачу верно

Решение: В случае а) при вычерчивании графа вершина А 5 раз являлась про-ходной (то есть в неё 5 раз пришли и 5 раз вышли). Ясно, что в этом случае сте-пень вершины равна 10. В случаях b) и c) вершина А 4 раза была проходной и один раз – концевой (начальной или конечной). Поэтому её степень равна 9. В случае d) вершина А дважды была концевой и 4 раза – проходной. Следователь-но, её степень равна 8.

Ответ: a) 10 b) 9 c) 9 d) 8

Задача №2

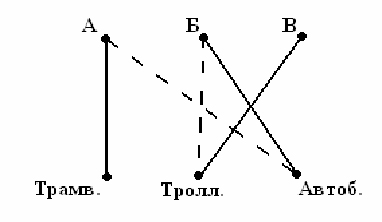
Друзья Алеша, Боря и Витя учатся в одном классе. Один из них ездит домой из школы на автобусе, другой на трамвае, а третий на троллейбусе. Однажды после уроков Алеша пошел проводить своего друга до остановки автобуса. Когда мимо них проходил троллейбус, третий друг крикнул из окна: «Боря, ты забыл в школе тетрадку!» Кто на чем ездит домой?

Команда 025 "Смежные вершины" решила задачу верно

Команда 061 "Графство "жареных семечек" решила задачу верно

Решение: Если Алёша пошёл провожать друга на автобус, значит, он не ездит на автобусе (это отмечено пунктиром). Если ехавший в троллейбусе кричал Боре, значит, Боря ездит не на троллейбусе, а на автобусе. Витя ехал на троллейбусе, так как Алёша и Боря стояли на остановке. Алёша ездит на трамвае.

Ответ: Алёша на трамвае Боря на автобусе Витя на троллейбусе

Задача №3

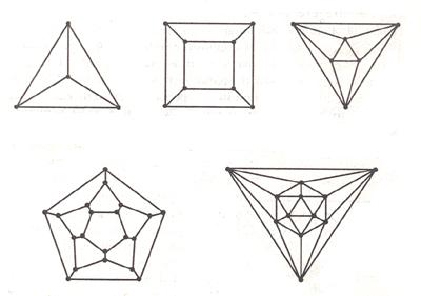
Существует ровно 5 типов правильных многогранников (тетраэдр, куб, октаэдр, додекаэдр, икосаэдр). Сможет ли муха последовательно обойти все ребра каждого многогранника, не проходя дважды по одному ребру. Подпрыгивать и пролетать с места на место не разрешается.

Команда 025 "Смежные вершины" решила задачу верно

Команда 061 "Графство "жареных семечек" решила задачу частично

Решение: Графы, образованные вершинами и рёбрами этих многогранников, на-зываются платоновыми графами. На плоскости они изображаются, как на пред-ставленном рисунке. Только у графа октаэдра, все его вершины имеют четвёр-тую степень. Все остальные графы имеют нечётные вершины. Поэтому их нельзя начертить одним росчерком пера.

Ответ: только у октаэдра.

Задача №4

В некоторой стране 10 городов, причем каждый соединен с каждым дорогой. какое наибольшее число дорог можно закрыть на ремонт так, чтобы из каждого города можно было проехать в каждый?

Команда 025 "Смежные вершины" решила задачу верно

Команда 061 "Графство "жареных семечек" решила задачу верно

Решение: Граф дорог в государстве является полным графом с десятью вершинном. Кол-во рёбер вычисляется по формуле n(n-1):2, то есть 45 рёбер. Удаляем рёбра в графе до тех пор, пока оно не превратится в дерево. Дерево имеет десять вершин и n-1 ребер, то есть 9. Следовательно, необходимо закрыть на ремонт 45-9=36 дорог.

Ответ: 36 дорог можно закрыть на ремонт.

Задача №5

В спортивный лагерь Ольга взяла 4 футболки, юбку, шорты и брюки, а Света - 7 платьев, 2 футболки, шорты и брюки. У кого из девочек больше нарядов?

Команда 025 "Смежные вершины" решила задачу верно

Команда 061 "Графство "жареных семечек" решила задачу верно

Решение: Составим графы, соответствующие условию задачи, для Оли и Светы. По схеме видно, что у Оли 3*4=12 комплектов нарядов, а у Светы 2*2+7=11 комплектов.

Ответ: у Оли больше.

Команда 053 "ЛОГО"

Задача 1. Сколько различных обедов П. И. Чичиков мог насчитать из блюд, выставленных на столе у П.П. Петуха, если бы на каждый обед выбирать только одно холодное блюдо, одно первое, одно второе, одно третье? На столе у П. П. Петуха на этот раз были выставлены из холодных блюд студень с хреном, свежая икра стерляжья, свежепосоленная белужина; на первое – уха из стерлядей, щи с грибами; на второе – осетрина жаренная, теленок, жаренный на вертеле; на третье – арбузы, груши.

Решение: 3×2×2×2=24 различных обедов.
Ответ: 24.

Команда 005 "Графство №90" решила задачу правильно
Команда 006 "ГрафУм" решила задачу правильно
Команда 008 "Лидер" решила задачу неправильно
Команда 011 "ГрафОграфы" решила задачу неправильно
Команда 025 "Смежные вершины" решила задачу правильно
Команда 061 "Графство "жареных семечек" решила задачу правильно
Команда 062 "Альтаир" решила задачу неправильно

Задача 2. 25 борцов играют по олимпийской системе (проигравший борец выбывает). За какое наименьшее количество встреч можно определить победителя?

Решение: После каждой встречи один борец выбывает. В конце остаётся 1 борец, значит, выбыть должно 24.
Ответ: 24.

Команда 005 "Графство №90" решила задачу правильно
Команда 006 "ГрафУм" решила задачу правильно
Команда 008 "Лидер" дала правильный ответ
Команда 011 "ГрафОграфы" решила задачу неправильно
Команда 025 "Смежные вершины" решила задачу правильно
Команда 061 "Графство "жареных семечек" решила задачу правильно
Команда 062 "Альтаир" решила задачу неправильно

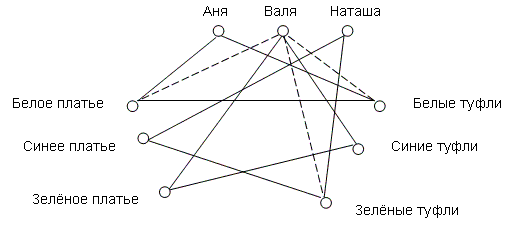
Задача 3. Три подруги Аня, Валя, Наташа вышли в белом, зелёном и синем платьях. Их туфли были одного из тех же трёх цветов. Известно, что только у Ани цвета платья и туфель совпадают. Ни платья, ни туфли Вали не были белыми. Наташа была в зелёных туфлях. Определите цвет платья и туфель каждой из подруг.

Решение: Условимся имена, цвета платья и туфель изображать точками, а отношения между ними – отрезками. Если «да» - отрезок сплошной, «нет» - штриховой.

У Вали не белые туфли, у Вали не зелёные (они у Наташи) => единственная возможность: у Вали – синие туфли.
У Ани – белые туфли. У Ани цвет туфель и платья совпадают => у Ани белое платье.
Известно, что только у Ани туфли и платье по цвету совпали. Значит, у Вали и Наташи не совпали => у Вали – зелёное платье, у Наташи – синее.

Ответ: Аня в белом платье и в белых туфлях, Валя в зелёном платье и в синих туфлях, Наташа в синем платье и в зеленых туфлях.

Команда 005 "Графство №90" дала правильный ответ
Команда 006 "ГрафУм" дала правильный ответ
Команда 008 "Лидер" решила задачу правильно
Команда 011 "ГрафОграфы" дала правильный ответ
Команда 025 "Смежные вершины" решила задачу правильно
Команда 040 "Львы" решила задачу правильно
Команда 061 "Графство "жареных семечек" решила задачу правильно
Команда 062 "Альтаир" решила задачу правильно

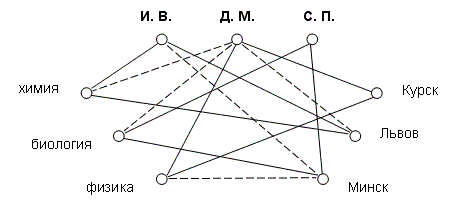
Задача 4. Три учительницы - Ирина Васильевна, Дарья Михайловна и Софья Петровна - преподают различные предметы (химию, биологию, физику) в школах Минска, Львова и Курска. Известно: а) Ирина Васильевна работает не в Минске, а Дарья Михайловна - не во Львове; б) та, которая живет в Минске, преподаёт не физику; в) работающая во Львове, преподает химию; г) Дарья Михайловна преподает не биологию. Определить кто, где и кем работает.

Решение: По условию задачи та из учительниц, которая живёт во Львове, преподаёт химию, но Д. М. не живёт во Львове => она не преподает химию => Д. М. преподаёт физику. По условию та, которая живёт в Минске, преподаёт не физику, но Д. М. преподаёт физику => она не живёт в Минске => Д. М. живёт в Курске. Так как в Минске не живут И. В. и Д. М. => в Минске живёт С. П. => И. В. живёт во Львове и преподаёт химию. С. П. преподаёт биологию в Минске.

Ответ: И. В. преподают химию во Львове; Д. М. – физику в Курске; С.П. – биологию в Минске.

Команда 005 "Графство №90" дала правильный ответ
Команда 006 "ГрафУм" дала правильный ответ
Команда 008 "Лидер" решила задачу неправильно
Команда 011 "ГрафОграфы" решила задачу правильно
Команда 025 "Смежные вершины" решила задачу правильно
Команда 040 "Львы" решила задачу правильно
Команда 061 "Графство "жареных семечек" решила задачу правильно
Команда 062 "Альтаир" решила задачу неправильно

Задача 5. На столе лежат журналы. Каждый посетитель просмотрел два журнала; каждый журнал просмотрели три человека; для каждой пары журналов есть только один посетитель, который их просмотрел. Сколько журналов и сколько посетителей?

Решение: Обозначим журнал точкой, а посетителя отрезком, выходящим из этой точки, получим полный граф, степень каждой вершины которого равна 3. Значит, у него 4 вершины и 6 рёбер.

Ответ: 4 журнала, 6 посетителей.

Команда 008 "Лидер" решила задачу правильно
Команда 011 "ГрафОграфы" решила задачу неправильно
Команда 025 "Смежные вершины" решила задачу правильно
Команда 040 "Львы" решила задачу правильно
Команда 061 "Графство "жареных семечек" решила задачу правильно

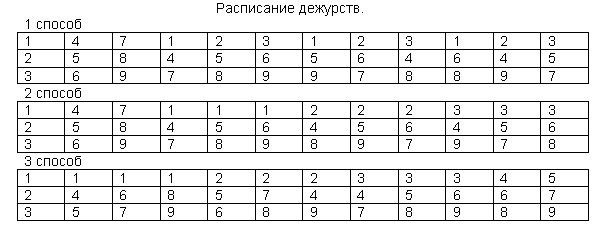
Задача 6. В походе, который длился 12 дней, участвовали 9 человек. Каждый день дежурили 3 человека. При этом дежурные ссорились друг с другом, и никакие двое из них не хотели больше ни разу дежурить вместе. Тем не менее, участники похода утверждают, что все 12 дней им удавалось назначать тройки дежурных с учётом этого требования. Составьте расписание дежурств.

Решение: Участники похода обозначены цифрами от 1 до 9, каждый столбец соответствует тройке дежурных.

Команда 005 "Графство №90" решила задачу неправильно
Команда 006 "ГрафУм" решила задачу неправильно
Команда 011 "ГрафОграфы" решила задачу правильно
Команда 025 "Смежные вершины" решила задачу правильно
Команда 061 "Графство "жареных семечек" решила задачу правильно

Решения задач присылайте на: sas2589@yandex.ru --Янина Ирина Владимировна 21:42, 3 декабря 2007 (UZT)

Команда 061 "Графство "жареных семечек""

MLB1@yandex.ru

Задача №1.

Несколько одноклассников организовали турнир по шашкам. Каждый участник турнира сыграл с каждым по одной партии. За выигрыш присуждали 2 очка, за ничью – 1 очко, за проигрыш – 0 очков. Пять самых слабых игроков набрали вместе 22 очка – в 4 раза меньше, чем остальные участники, вместе взятые. Сколько было участников турнира?

Представила правильное решение Команда 025

Представила правильное решение Команда 053

Решение

Всего участники турнира могли набрать 22*4+22=22*5=110 очков. У нас получается полный граф, в котором вершины – игроки, а ребра – партии, каждая партия 2 балла, значит всего партий 110:2=55. Пусть игроков (вершин) Х, тогда число сыгранных каждым партий (степень вершины) - (Х-1). Всего партий (ребер) 55. Используя свойство полного графа, составим уравнение: Х*(Х-1)/2=55. Решим его.

Х=-10, Х=11. Х= -10 не удовлетворяет условию задачи.

Итак, участников турнира 11 человек.

Ответ: 11 человек.

Задача №2.

Последовательность аn задана с помощью рекуррентной формулы: Доказать, что в полном графе с вершиной, ребра которого окрашены в n цветов, найдется треугольник с одноцветными сторонами.

Задача №3.

Как-то в минуту отдыха друзья-мушкетеры: Атос, Портос, Арамис и д’Артаньян решили помериться силой при перетягивании каната. Портос с д’Артаньяном легко перетянули Атоса и Арамиса. Но когда Портос встал в паре с Атосом, то победа против Арамиса с д’Артаньяном досталась им уже не так легко. Когда же Портос с Арамисом оказались против Атоса с д’Артаньяном, то ни одна из этих пар не смогла одолеть друг друга. Можете ли вы определить как мушкетеры распределяются по силе?

Представила правильное решение Команда 025

Представила правильный ответ Команда 053

Решение:Пусть Атос - №1, Портос- №2, Арамис- №3 и д’Артаньян- №4. Пары: (2;4) с (1;3); (2;1) с (3;4); (2;3) с (1;4).

В каждом поединке, где нет проигрыша есть Портос (№2). Значит, он самый сильный, д’Артаньян и Атос проиграли по только одному разу, но д’Артаньян в паре с Портосом уверенно обыграл пару Атоса с Арамисом в отличии от Атоса с Портосом, которые ели-ели выйграли пару д’Артаньян и Арамиса. Значит, д’Артаньян на втором месте по силе. Атос на третьем, а Арамис, допустивший больше всех проигрышей на последнем.

Построим граф. Вершины – мушкетеры. Ребра графа - ориентированные, причем сплошная линия – уверенная победа, пунктиром – трудная победа. Из графа видно, что Больше всего побед у Портоса, затем идет д’Артаньян, затем Атос и замыкает Арамис.

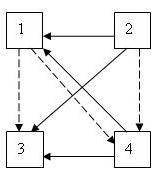
Ответ: Портос, затем идет д’Артаньян, затем Атос и замыкает Арамис.

Задача №4.

В одной из школ 20 раз проводился кружок по астрономии. На каждом занятии присутствовало ровно пять школьников, причем никакие два школьника не встречались на кружке более одного раза. Докажите, что всего на кружке побывало не менее 20 школьников.

Представила правильное решение Команда 025

Представила неверное решение Команда 040

Решение:

Из пяти школьников можно составить ровно 10 различных пар.

(1-2), (1-3), (1-4).(1-5), (2,3), (2-4), (2-5), (3-4),(3-5), (4-5). Т.к. никакие два школьника не были одновременно более чем на одном занятии кружка, то получается, что из всех ходивших на кружок можно составить не менее чем 10*20=200 пар. Предположим, что на кружке побывало 19 школьников. Тогда каждый школьник мог быть связан парами с 18-ю другими. Получаем полный граф, где 19 вершин, степень которых 18. Тогда ребер (различных пар) в этом графе 19*18/2=171. Но 171 меньше 200. Противоречие. Значит, на кружке побывало не менее 20 школьников.

Задача №5.

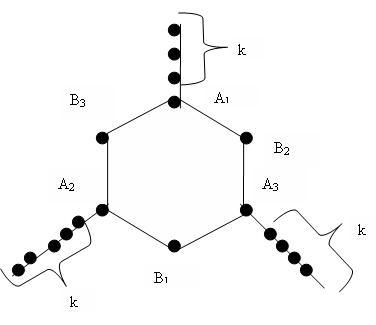
В игре «Десант» две армии захватывают страну. Они ходят по очереди, каждым ходом занимая один из свободных городов. Первый свой город армия захватывает с воздуха, а каждым следующим ходом она может захватить любой город, соединенный дорогой с каким-нибудь уже занятым этой армией городом. Если таких городов нет, армия прекращает свои боевые действия (при этом, возможно, другая армия свои действия продолжает). Найдется ли такая схема городов и дорог, что армия, ходящая второй, сможет захватить более половины всех городов, как бы ни действовала первая армия? (Число городов конечно, каждая дорога соединяет ровно два города).

Решение:

Рассмотрим страну, карта которой представлена графом (точки – города, отрезки – дороги). Покажем, что второй армии всегда удастся захватить хотя бы два города Аi . Действительно, если первая армия первым ходом занимает город на одной из «веток», то вторая армия должна занять соответствующий этой «ветке» город Аi; если первая армия занимает Аl , то вторая – Bl. Если первая выбирает город Bl, то вторая – один из городов Аj, соединенный дорогой с Вl. Дальнейшие действия очевидны. Итак, после прекращения боевых действий вторая армия занимает хотя бы два города Аi, а значит, и две соответствующие «ветки», и город Вj между занятыми городами Аi , всего по крайней мере 2k+3 городов. Поэтому доля городов, захваченных второй армией, не менее (2k+3)/(3k+6). Уже при k=1 это число больше ½.

Задача №6.

В шахматном турнире участвовали n шахматистов – мастера и гроссмейстеры. После окончания турнира оказалось, что каждый участник ровно половину своих очков набрал в партиях против мастеров. Докажите, что n - квадрат целого числа.

Представила не совсем верное решение Команда 025

Представила правильное решение Команда 053

Решение:

Пусть было m мастеров и g гроссмейстеров. Тогда m + g = n. Все мастера играют друг с другом. Образуется полный граф. Аналогично, все гроссмейстеры тоже играют друг с другом, их игры тоже можно представить в виде графа. Как бы ни окончилась партия между двумя партнерами, суммарное число очков, набранных ими, увеличится на 1. Значит, мастера в партиях с мастерами набрали m(m-1)/2 очков. Поскольку каждый мастер половину своих очков набрал в партиях с гроссмейстерами, общее число очков, набранных мастерами в партиях против гроссмейстеров, равно m(m-1)/2. Точно так же гроссмейстеры в партиях против мастеров набрали g(g-1)/2 очков. Число партий, в которых мастер играл с гроссмейстером, равно mg.

--Графство "жареных семечек" 061 15:51, 7 декабря 2007 (UZT)

Команда 062 "Альтаир"

Решения присылать по адресу ele-na00@mail.ru Альтаир 062

1. Какое наибольшее число веревочек можно перерезать в квадратной сетке 8х8 ячеек, чтобы сетка еще не распалась на куски? Веревочкой является каждый кусок веревки между узлами сетки. В решении следует доказать, что при любом разрезании больше веревочек, чем вы указали, разрезать не удастся.

Команда 025 "Смежные вершины" решила задачу верно

Команда 061 "Графство "жареных семечек"" решила задачу верно

Команда 008 дала правильный ответ

Команды 005, 006 дали неправильный ответ, т.к. неверно поняли условие

Команда 040 дала неправильный ответ

Команда 053 решила задачу верно

2. У Винни-Пуха есть 3 сорта варенья - яблочное, вишневое и сливовое. Он составляем меню завтрака так, чтобы каждый раз набор сортов варенья был различный. Через сколько дней набор точно повторится? (Хотя бы один сорт варенья на завтрак должен быть).

Команда 025 "Смежные вершины" решила задачу верно

Команда 061 "Графство "жареных семечек"" решила задачу верно

Команда 008 дала неправильный ответ

Команды 005, 006 дали неправильный ответ

Команда 053 решила задачу верно

3. Как рассадить за 3 парты 6 детей, если Лена не любит Ваню, Маша не любит Петю, а Петя не любит Лену. Гена и Ира сказали, что они любят всех.

Команда 061 "Графство "жареных семечек"" решила задачу верно

Команда 025 "Смежные вершины" решила задачу верно

Команда 063 "Форсаж" решила задачу верно

Команда 040 решила задачу верно

Команда 053 решила задачу верно

Решение 1: Сетка это граф с 9*9=81 вершинами и количеством ребер 8*9+9*8=72+72=144. Мы можем разрезать веревочки до тех пор, пока граф не превратится в дерево. У дерева будет 81 вершина, а количество ребер вычисляется по формуле (n-1), т.е будет равно 80. Так как из 144 ребер осталось 80, значит, разрезано 64. Ответ: можно перерезать 64 веревочки

Задача №2. Винни-Пух может запланировать на завтрак один сорт варенья, таким образом он может завтракать 3 дня (яблочное, вишневое, сливовое) Винни-Пух может запланировать на завтрак два сорта варенья, значит 3 дня Винни-Пух может завтракать двумя сортами варенья Винни-Пух может запланировать на завтрак 3 сорта варенья, возможен только один вариант (все три имеющиеся сорта). Таким образом, получаем, что 7 дней Вини-Пух может завтракать различными наборами, а на 8-ой придется повторить какой-нибудь вариант. Ответ: через 7 дней

Задача №3. Решение: Лена может сидеть только с Геной, тогда Маша с Ваней, а Петя с Ирой. Ответ: Лена с Геной, Маша с Ваней, а Петя с Ирой.

Команда 063 "Форсаж 063"

Решения присылать по адресу ele-na00@mail.ru Форсаж 063

1. В государстве 15 областей. Области считаются соседями, если у них есть общая граница. Может ли у каждой области быть ровно 7 соседей?

Команда 025 "Смежные вершины" решила задачу верно

Команда 005 "Графство №90 дала правильный ответ

Команда 006 "ГрафУм" дала правильный ответ

Команда 062 "Альтаир" решила задачу верно

Команда 061 "Графство "жареных семечек"" решила задачу верно

Команда 040 решила задачу верно

Команда 053 решила задачу верно

Задача №1 Решение: Если мы построим граф, где вершинами будут области, а ребра будут отображать наличие границы между государствами, то получиться, что все вершины будут иметь нечетную степень Такой граф начертить нельзя, потому что граф с нечётным числом нечётных вершин начертить невозможно. Ответ: Нет, не может.

2. На ралли Волгодонск - Тольятти до финиша добрались 6 машин. Сколько существует вариантов заполнения 1-го, 2-го и 3-го мест?

Решение 2.Первое место могут занять 6 экипажей, 2-е любой из 5 оставшихся, 3-е любой из 4 оставшихся. Всего 120=6*5*4 вариантов.

Команда 025 "Смежные вершины" решила задачу верно

Команда 005 "Графство №90 дала правильный ответ

Команда 006 "ГрафУм" дала правильный ответ

Команда 062 "Альтаир" решила задачу верно

Команда 061 "Графство "жареных семечек" решила задачу верно

Команда 040 решила задачу неверно

Команда 053 решила задачу верно