Семинар ДООМ "Использование занимательных задач на уроках математики"

Увеличение умственной нагрузки на уроках математики заставляет задуматься над тем, как поддержать у учащихся интерес к изучаемому материалу, их активность на протяжении всего урока. В связи с этим каждым учителем ведутся поиски новых эффективных методов обучения и таких методических приемов, которые активизировали бы мысль школьника, стимулировали бы их к самостоятельному приобретению знаний. Многие учителя, и я принадлежу к их числу, высказываются за привлечение в учебный процесс элементов игры. Тихомирова Лариса Николаевна, ID 270

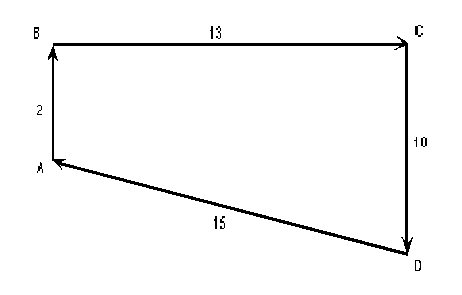
Возможность и целесообразность использования игровых ситуаций на уроках математики в процессе изучения и закрепления нового материала различны в зависимости от дидактических целей урока. В большинстве случаев они применяются в качестве вспомогательного средства для возбуждения познавательного интереса и создания проблемных ситуаций. Это настраивает учащихся на изучение определенного материала. Для создания игровых ситуаций на уроках математики используются исторические экскурсы, жизненные факты, отрывки из литературных произведений, занимательные задачи. Рассмотрим решение одной из занимательных задач с использованием текста литературного произведения на уроке алгебры В начале урока учитель знакомит учащихся с рассказом Л.Н. Толстого «Много ли человеку земли надо». О том, как крестьянин Пахом, который мечтал о собственной земле и собрал наконец желанную сумму, предстал перед требованием старшины: «Сколько за день земли обойдешь, вся твоя будет за 1000р. Но, если к заходу солнца не возвратишься на место, с которого вышел, пропали твои деньги». Выбежал рано утром Пахом, прибежал на место, обежав четырехугольник периметром P = 40км, и упал без чувств.

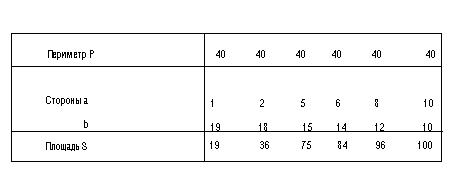
S = (2+10)/2*13 = 78(кв. км) Наибольшую ли площадь при данном периметре получил Пахом? Трем учащимся предлагается выйти к доске и начертить четырехугольник с P = 40 и наибольшей площадью. Учащиеся пробуют чертить известные им четырехугольники: трапецию, ромб, прямоугольник, квадрат. Для подкрепления догадки учитель предлагает составить таблицу для вычисления площадей прямоугольников с различными длинами сторон.

Вывод. Из всех прямоугольников данного периметра наибольшую площадь имеет квадрат. Пахом, например, мог бы пройти всего 36 км (P = 9*4=36 км) и иметь участок площадью S = 9*9 = 81(кв. км) После этого учащиеся составляют функцию и исследуют ее на экстремум. Если стороны прямоугольника x и y, то x + y = 20; S = xy; S = x(20 - x); S` = -2x + 20; S` = 0, x = 10.