Семинар ДООМ Тайны квадрата

Команды: АксиомаIDm014,ТеоремикиIDm013,БесконечностьIDm029.

Любой квадрат можно разделить на равные клетки, при этом количество строк и столбцов будет одинаково. Если по количеству клеток

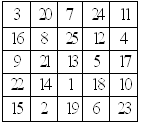
взять числа подряд, начиная с единицы, и вписать их по одному в каждую клетку так, чтобы сумма чисел в каждом столбце, в каждой строке и в каждой диагонали были равны, то такой квадрат называется магическим. Магические квадраты появились на Востоке в незапамятные времена. В Европе о них узнали намного позже, примерно пятьсот лет тому назад. Сначала этим квадратам приписывали таинственную силу, считали, что они могут уберечь от несчастий. Потом ими заинтересовались математики. Многие известные ученые занимались магическими квадратами. На рисунке 1 один из магических квадратов в нем 25 клеток (т.е. магический квадрат порядка 5X5), в которые вписаны числа от 1 до 25. Не поленитесь проверить, что этот квадрат действительно

Постройте сами магический квадрат порядка 3X3 (рис. 2) вписав в него числа от 1 до 9. Подсказка: сначала выясните например,

внимательно рассмотрев квадрат 5X5 на рисунке 1 какое число необходимо вписать в центральную клетку. Попробуйте, не вписывая числа в квадрат, заранее, узнать чему должна равняться сумма чисел в каждой строке, каждом столбце или диагонали квадрата

Надеемся, что вы справились с построением магического квадрата 3X3. Такой квадрат существует только один. Квадраты, которые

получаются путем поворота изначального квадрата или перестановкой его строчек или столбцов, считаются одинаковыми. Построить магический квадрат большего порядка, не имея способа построения, довольно сложно. Существует много различных методов построения магических квадратов. На рисунке вы видите очень красивый способ построения магических квадратов нечетных порядков. Разберитесь в этом способе по рисунку. Впишите красные цифры в красные квадратики, зеленые — в зеленые, синие — в синие, а желтые — в желтые. И получится магический квадрат. Этот метод называется методом террас или индийским методом, он был известен еще в XIII веке. На рисунке показано построение одного из магического квадратов порядка 5X5. Магических квадратов такого порядка очень много, даже не известно точно сколько.

Теперь, пользуясь методом террас, самостоятельно постройте магический квадрат порядка 7X7.

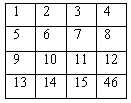
Методы построения магических квадратов четных порядков достаточно сложны. Постройте магический квадрат порядка 4X4. Прежде чем

начать построение, вычислите чему должна равняться сумма чисел в каждой строке, каждом столбце или диагонали готового магического квадрата. Впишем в квадрат числа от 1 до 16 в их обычном порядке. Найдите в этом квадрате такие четыре пары чисел, что если внутри каждой пары поменять числа местами, то получится магический квадрат. Таким образом вы построите один из магических квадратов порядка 4X4, всего разных магических квадратов такого порядка — 880