Семинар ДООМ Тайны квадрата

Команды: АксиомаIDm014,ТеоремикиIDm013,БесконечностьIDm029.

Любой квадрат можно разделить на равные клетки, при этом количество строк и столбцов будет одинаково. Если по количеству клеток

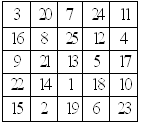
взять числа подряд, начиная с единицы, и вписать их по одному в каждую клетку так, чтобы сумма чисел в каждом столбце, в каждой строке и в каждой диагонали были равны, то такой квадрат называется магическим. Магические квадраты появились на Востоке в незапамятные времена. В Европе о них узнали намного позже, примерно пятьсот лет тому назад. Сначала этим квадратам приписывали таинственную силу, считали, что они могут уберечь от несчастий. Потом ими заинтересовались математики. Многие известные ученые занимались магическими квадратами. На рисунке 1 один из магических квадратов в нем 25 клеток (т.е. магический квадрат порядка 5X5), в которые вписаны числа от 1 до 25. Не поленитесь проверить, что этот квадрат действительно

Постройте сами магический квадрат порядка 3X3 (рис. 2) вписав в него числа от 1 до 9. Подсказка: сначала выясните например,

внимательно рассмотрев квадрат 5X5 на рисунке 1 какое число необходимо вписать в центральную клетку. Попробуйте, не вписывая числа в квадрат, заранее, узнать чему должна равняться сумма чисел в каждой строке, каждом столбце или диагонали квадрата

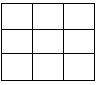
Надеемся, что вы справились с построением магического квадрата 3X3. Такой квадрат существует только один. Квадраты, которые

получаются путем поворота изначального квадрата или перестановкой его строчек или столбцов, считаются одинаковыми. Построить магический квадрат большего порядка, не имея способа построения, довольно сложно. Существует много различных методов построения магических квадратов. На рисунке вы видите очень красивый способ построения магических квадратов нечетных порядков. Разберитесь в этом способе по рисунку. Впишите красные цифры в красные квадратики, зеленые — в зеленые, синие — в синие, а желтые — в желтые. И получится магический квадрат. Этот метод называется методом террас или индийским методом, он был известен еще в XIII веке. На рисунке показано построение одного из магического квадратов порядка 5X5. Магических квадратов такого порядка очень много, даже не известно точно сколько.

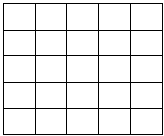
Теперь, пользуясь методом террас, самостоятельно постройте магический квадрат порядка 7X7.

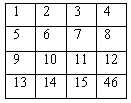
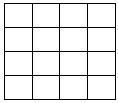
Методы построения магических квадратов четных порядков достаточно сложны. Постройте магический квадрат порядка 4X4. Прежде чем

начать построение, вычислите чему должна равняться сумма чисел в каждой строке, каждом столбце или диагонали готового магического квадрата. Впишем в квадрат числа от 1 до 16 в их обычном порядке. Найдите в этом квадрате такие четыре пары чисел, что если внутри каждой пары поменять числа местами, то получится магический квадрат. Таким образом вы построите один из магических квадратов порядка 4X4, всего разных магических квадратов такого порядка — 880

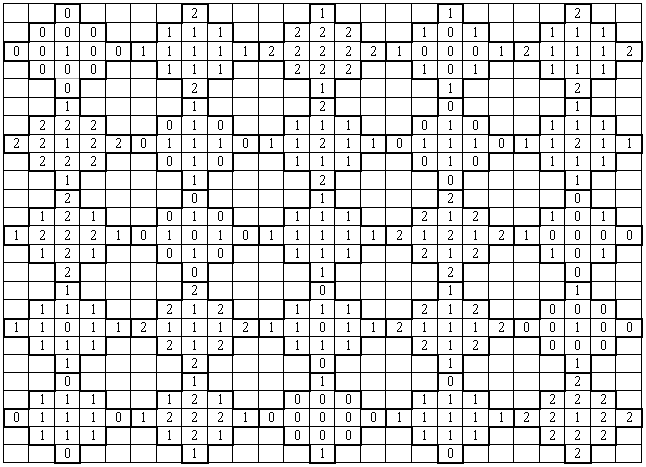
Если вы сложите цифры внутри каждой тринадцатиклеточной "зубчатой" фигуры, очерченной более жирной линией, то получится магический

квадрат порядка 5X5. Раскрасьте нулики в зеленый цвет, единицы в красный цвет, а двойки в желтый цвет, и тогда вы увидите красивую мозаику.

Предполагают, что великий математик Леонард Эйлер придумал эту головоломку присутствуя на одном из петербургских парадов. Вот она:

на площади находятся 36 офицеров, среди них 6 уланов, 6 драгунов, 6 гусаров, 6 кирасиров, 6 кавалергардов и 6 гренадеров, причем среди 6 офицеров каждого рода войск присутствуют офицеры б чинов, т.е. один генерал, один полковник, один майор, один капитан, один поручик и один подпоручик. Можно ли выстроить этих военных в виде квадрата 6X6 так, чтобы в каждом ряду и в каждой колонне встречались офицеры всех шести родов войск и всех шести чинов. Оказалось, что эта головоломка не имеет решения. Решение головоломки, когда по тем же правилам необходимо разложить 9 цветков, где род войск — это вид цветка, а чин военного — цвет цветка, изображено на первой странице обложки. В последние годы жизни Леонард Эйлер написал большой труд о магических квадратах нового типа. Сейчас такие магические квадраты принято называть латинскими, потому что Эйлер вписывал в их клетки не цифры, а латинские буквы. Пример латинского квадрата изображен на рисунке 1. Двадцать пять клеток в нем заполнены пятью латинскими буквами А, В, С, D, F, причем в каждой строчке и в каждом столбце буквы не повторяются. На рисунке 2 изображен другой латинский квадрат, клетки которого окрашены впять цветов. Наложите эти два квадрата друг на друга и нарисуйте то, что получится в квадрате на рисунке 3. Окажется, что каждая латинская буква появится один и только один раз в паре с каждым цветом. Два или более латинских квадратов, которые можно так скомбинировать, называются ортогональными квадратами. Как теперь понятно, на первой странице обложки изображена пара наложенных друг на друга ортогональных латинских квадратов третьего порядка.

У мастера имелись девять плиток: три синие, три красные и три желтые. Он решил выложить на стене из этих девяти плиток квадрат.

Причем т ак, чтобы в каждой строке и в каждом столбце была бы одна синяя, одна красная и одна желтая плитка. И тут мастер задумался: сколько таких разных квадратов из девяти плиток он мог бы выложить? Помогите мастеру и нарисуйте все варианты расстановки плиток.

Какие слова надо вписать в пустые клетки первого и второго квадратов?