Семинар ДООМ Четырехугольники на координатной плоскости

Учитель математики:

Участник:Лосинская Наталья Викторовна МОУ гимназия № 48 Тольятти, 2009 Искатели IDm033

Тема урока:

Четырехугольники на координатной плоскости.

Тип урока:

урок закрепления ранее изученного материала.

Цель урока:

Изучить свойство вершин параллелограмма на координатной плоскости.

Задачи:

1)отработка навыков по применению формул координат середины отрезка и расстояния между точками через решение задач;
2)выявление взаимосвязи тем геометрии "Четырехугольники" 8 кл. и "Метод координат" 9 кл.; применение метода координат для расширения объема знаний;
3)повторение теоретического материала по теме "Четырехугольники" в ходе решения задач;
4)совершенствование вычислительной культуры учащихся;
5)развитие навыков творческого мышления учащихся: развитие логического мышления, памяти, умения анализировать и обобщать, сравнивать и находить аналогии;
6)воспитание культуры речи учащихся;
7)формирование положительных мотивов учения;
8) формирование навыков организации учебной деятельности учащихся.

Оборудование урока:

1)содержание задач учебника Л.С. Атанасяна "Геометрия 7-9";
2)справочник, рабочая тетрадь, инструменты;
3)портрет Рене Декарта;
4)медиапрезентация «Метод координат».

Содержание урока:

1.Организационный момент (1 мин.)
2.Актуализация ранее полученных знаний (5 мин.)
3.Изучение нового материала (15 мин.)
4.Закрепление изученного материала (16 мин.)
5.Подведение итогов урока. Задание на дом.(3 мин.)

I.Организационный момент

Учитель:
Эпиграфом урока сегодня будет высказывание Д. Пойа "Наиболее глубокий след оставляет то, что тебе удалось открыть". Проверить справедливость этих слов нам поможет этот урок, на котором мы проследим связь двух тем "Четырехугольники" и "Метод координат", т.к. геометрия - это наука со взаимосвязанными темами. А поможет нам в этом прямоугольная система координат.

II. Актуализация ранее полученных знаний.

На фоне демонстрации презентация Метод координат тучащиеся повторяют формулы координат середины отрезка и расстояния между точками.
"Не так уж и трудно задачи решать:
Проблема дает вдохновенье
Искусство же в том, чтоб суметь отыскать
Задачу, когда есть решенье".
П. Хэйн

Задача №1:

Доказать, что сумма абсцисс середин сторон треугольника равна сумме абсцисс вершин треугольника (аналогично для ординат).

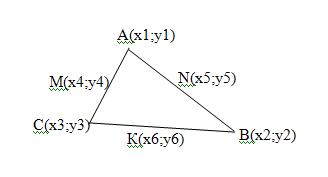
Дано: треугольник ABC, M, N, K – середины AC, AB, BC, А(0;1), В(1;-4), С(5;2)
Доказать:
х4 + х5 + х6 = х1 + х2 + х3,
у4 + у5 + у6 = у1 + у2 + у3.
Доказательство:
х4 = (0 + 5)/2 = 2,5, х5 = (0 + 1)/2 = 0, 5, х6 = (1 + 5)/2 = 3;
х4 + х5 + х6 = 2,5 + 0,5 + 3 = 6, х1 + х2 + х3 = 0 + 1 + 5 = 6, ч.т.д.
Аналогично для ординат точек.

Задача №2

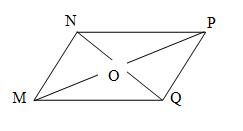
Дано: МNPQ – четырехугольник
М (1;1), N (6;1), Р(7;4), Q (2; 4).
Доказать: МNPQ - параллелограмм.
Вопрос: Какой признак параллелограмма мы будем использовать при решении задачи?
Ответ: Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник - параллелограмм.
Решение:
1) О – середина МР, то O(4; 2,5);
2)O – середина NQ, то O(4; 2,5); тогда МNРQ – параллелограмм (по признаку параллелограмма).

III. Изучение нового материала.

Учитель:
Мы доказали, что МNPQ - параллелограмм. Теперь устно выполните мое задание: Чему равна сумма абсцисс точек, которые являются концами диагонали МР и NQ?
Ответ:х = 8 = 8.
Вопрос:Чему равна сумма ординат диагоналей МР и NQ?
Ответ:у = 5 = 5.
Учитель: Путем вычислений мы получили, что сумма абсцисс концов одной диагонали параллелограмма равна сумме абсцисс концов другой диагонали, аналогично для ординат точек. Случаен ли этот факт?
Задача :Начертите произвольный параллелограмм в прямоугольной системе координат и определите координаты вершин параллелограмма. Каждый для своего чертежа найдите сумму абсцисс концов одной диагонали и сумму абсцисс концов другой диагонали. Сравните эти результаты.
Ответ:Равны, т.е. сумма абсцисс концов одной диагонали равна сумме абсцисс концов другой диагонали параллелограмма. Учитель: Найдите сумму ординат концов диагоналей параллелограмма. Сравните эти числа. Ответ: Равны, т.е. сумма ординат концов одной диагонали равна сумме ординат концов другой диагонали параллелограмма. Учитель: Значит, говорить о случайности данного факта уже нельзя. Можно уже говорить о свойстве параллелограмма, если известны координаты вершин. Накопленные факты позволяют нам выдвинуть гипотезу.
ГИПОТЕЗА: В параллелограмме сумма абсцисс концов одной диагонали равна сумме абсцисс концов другой диагонали, сумма ординат концов одной диагонали равна сумме ординат концов другой диагонали. Но пока это только гипотеза, истинность которой надо проверить доказательством.
Учитель: Какое свойство параллелограмма нам поможет в доказательстве? Ответ: Диагонали параллелограмма точкой пересечения делятся пополам. Учитель: Действительно, при доказательстве используется это свойство параллелограмма и формула координат середины отрезка. Доказательство – будет частью вашего домашнего задания.
Учитель: Сформулируйте признак параллелограмма в декартовых координатах. Ответ: Если в четырехугольнике сумма абсцисс концов одной диагонали равна сумме абсцисс концов другой диагонали, сумма ординат концов одной диагонали равна сумме ординат концов другой диагонали, то этот четырехугольник – параллелограмм.

IV. Закрепление нового материала.

Учитель: Теперь посмотрим как это свойство параллелограмма применяется при решении задач - на практике. Устно выполним задание: АВСD – параллелограмм: А(–4; –3), В(5; –2), С(1; 2). Найдите координаты вершины D. Дано: АВСD – параллелограмм: А(–4; –3), В(5; –2), С(1; 2).
Найти: координаты вершины D.
Решение: - 4 + 1 = х + 5, - 3 + 2 = у + (-2), х = -8, у = 1 (по свойству параллелограмма).
Ответ:D(–8;1);
Учитель: Данная задача имела единственное решение. А сколько параллелограммов можно построить по трем точкам, не лежащим на одной прямой, если они являются вершинами параллелограмма? Ответ: три параллелограмма.

Задача № 1

Дано: АВСD – параллелограмм, К – точка пересечения диагоналей, А(–4; –3), В(5; –2), К(1; 2).
Найти: координаты вершин С и D.
Решение: 1)АВСВ – параллелограмм, К – середина АС и ВD, тогда 2) К – середина АС, то C(6;7); 3) ABCD – параллелограмм, тогда по свойству параллелограмма D(–3;6).
Ответ: C(6;7), D(–3;6).

Задача № 2:

Дано: ABCD – трапеция, AB|| DC, А(–4;–3), В(5;–2), С(6;7), D(–12;5), MN – средняя линия ABCD.
Найти: MN.
Учитель: Какие способы есть для решения данной задачи?
Ответ:
I. По определению средней линии трапеции.
II. По теореме о средней линии трапеции.
Учитель: Задание по вариантам:
I. Найти MN по определению средней линии трапеции;
II. МN по теореме о средней линии трапеции.

IV. Подведение итогов урока. Задание на дом.

Учитель: Сегодня на уроке мы проследили путь познания в математической науке: накопление фактов › выдвижение гипотезы › проверка истинности доказательством › построение теории › выход в практику. Мы с вами "открыли" свойство параллелограмма в декартовых координатах и учились применять это свойство при решении задач.
Задание на дом:
Доказательство свойства параллелограмма.
№ 951 (а) – доказать, что ABCD – прямоугольник.
№ 998 – ABCD – ромб.

Литература.

1. Л.С. Атанасян "Геометрия 7-9", М., 1998.
2. Ю.Г. Разбеглов "Путешествие по Пифагории или Тетрадь с печатной основой", 8 кл., Харьков, 1994.
3. Математика в школе № 5, 1995 Т.А. Иванова "Методология научного поиска - основа технологии развивающего обучения".
4. Математика в школе№ 3, 1994 Е. Феоктистов "Материал по теме "Декартовы координаты на плоскости".