Семинар ДООМ "План-конспект урока геометрии в 8 классе"

Участник:Тихомирова Лариса Николаевна,IDm038

Тема:Прямоугольник. Ромб. Квадрат.

Цели:

• Систематизировать и обобщить знания учащихся по изучаемой теме; совершенствовать навыки решения задач.

• Развивать умение наблюдать, сравнивать, обобщать, классифицировать, анализировать математические ситуации.

• Способствовать воспитанию таких качеств личности, как познавательная активность, самостоятельность, упорство в достижении цели.

Тип урока: обобщающий урок.

Оборудование:

1. Компьютер, проектор;

2. Набор разноцветных моделей ромба, квадрата, прямоугольника, параллелограмма для каждого ученика;

3. Карточки с текстами задач;

4. Боковая доска.

Структура урока:

1. Ознакомление с темой урока, постановка его целей (2 мин).

2. Первичное повторение и закрепление новых знаний и умений на уровне воспроизведения. (10 мин.).

3. Проверочный тест (8 мин.).

4. Систематизация и обобщение новых знаний и умений при выполнении познавательных заданий на преобразующем и творческом уровнях. (12 мин.).

5. Самостоятельная работа (8 мин.).

6. Подведение итогов урока (2 мин.).

7. Домашнее задание (3 мин.).

Ход урока.

1. Ознакомление с темой урока, постановка его целей. Вместе с дежурными учитель проверяет готовность класса к уроку, после чего сообщает тему урока и цели урока.

2. Первичное повторение и закрепление новых знаний и умений на уровне воспроизведения.

Систематизация теоретических знаний по пройденному материалу проходит в несколько этапов:

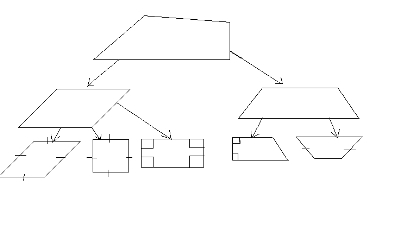
1) С помощью проектора на экран проецируется схема1.

Схема 1.

Учитель проводит фронтальное обсуждение по этой схеме.

Учитель: Почему на схеме 1 самый верхний четырехугольник изображен так, что ни сторон у него равных нет, ни углов?

Ученик: Потому что в определении четырехугольника ничего не сказано о равенстве сторон или углов.

Учитель: О чем говорят стрелки, проведенные от самого верхнего четырехугольника?

Ученик: О том, что среди четырехугольников можно выделить особые, имеющие больше характерных признаков, чем все остальные.

Учитель: Какие же это «особые четырехугольники»?

Ученик: Это параллелограммы (даются определения) и трапеции.

Учитель: Можно ли среди параллелограммов выделить такие, которые обладают какими - то дополнительными свойствами?

Ученик: Можно. Это ромбы и прямоугольники. Всеми свойствами у ромба и прямоугольника обладает квадрат (даются определения всех упомянутых фигур).

Закрепление: У каждого ученика на парте лежат разноцветные модели ромба, квадрата, прямоугольника и др. параллелограммов.

Учитель: Поднимите ту фигуру, которая обладает названным свойством:

а) имеет равные диагонали;

б) имеет равные противоположные углы;

в) имеет перпендикулярные диагонали;

г) имеет равные противоположные стороны;

д) углы, прилежащие к одной стороне, в сумме составляют 180°;

е) диагонали являются биссектрисами углов (ромб и квадрат);

ж) сумма всех углов равна 360°.

2. Проверочный тест: Учащиеся выполняют тест (Приложение 1) по вариантам. Листочки заранее розданы учащимся. Учащиеся должны прочитать задания теста, спроецированные с помощью проектора и записать код правильного ответа. Окончив работу, ученики обмениваются работами. С помощью проектора проверяется правильность ответов и выставляются оценки ( 6 зад.-«5»; 5 зад.-«4»; 4 зад.-«3»; менее 4 зад.- «2»).

Ответ:

1 вариант:

1 - в; 2 - г; 3 - б; 4 - г; 5 - в; 6 - в. 2 вариант:

1 - в; 2 - а; 3 - а; 4 - в; 5 - а; 6 - б.

4. Систематизация и обобщение новых знаний и умений при выполнении познавательных заданий на преобразующем и творческом уровнях.

Осуществляется в два этапа:

1) Во время обучения применению теоретических знаний в процессе решения задач. На партах у учащихся лежат тексты с заданиями.

Задание: Прочитав задачу, составьте чертеж, обозначьте на нем все данные, а также сведения, вытекающие из свойств или определения фигур. Рядом с чертежом сделайте необходимые вычисления, укажите свойства. После того как ребята обдумают решение, учитель открывает на доске сделанный заранее чертеж - заготовку и один из учеников рассказывает решение задачи.

Задача 1: Меньшая сторона прямоугольника равна 4 см и образует с диагональю угол 60°. Найдите диагонали прямоугольника.

Решение:

Диагонали прямоугольника равны и точкой пересечения делятся пополам. Следовательно: Δ ABO - равнобедренный, значит угол ABO = 60° Δ ABO - равносторонний, т.е. BO = AO = BA = 4 см, AC = 8 см и BD = 8 см.

Задача 2: Сумма трех углов параллелограмма равна 252°. Найдите углы параллелограмма.

Решение: Так как противолежащие углы параллелограмма равны, т.е. углы A = C, и углы B = D; Сумма углов, прилежащих к одной стороне параллелограмма, равна180°. По условию сумма углов A + B + C = 252°, но в любом четырехугольнике сумма углов равна 360°. Угол D = 360° - 252° = 108°, угол B = 108°, углы A = C = 180° - 108° = 72°.

Задача 3: Углы, образуемые стороной ромба с его диагональю, относятся как 4:5. Вычислить углы ромба.

Решение: Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов. Следовательно сумма углов 1 + 2 = 90°, тогда 90° / (4 + 5) = 10 - составляет 1 часть; 10° * 4 = 40 - составляет 4 части; 10° * 5 = 50° - составляют 5 частей, т.е. угол D = 40° * 2 = 80°, угол A = 50° * 2 = 100°. Значит углы B = D = 80°.

5. Самостоятельная работа.

1 вариант : Найдите углы ромба, если его диагонали составляют с его стороной углы, один из которых на 30° меньше другого.

2 вариант: Угол между диагоналями прямоугольника равен 80°. Найдите углы между диагональю прямоугольника и его сторонами.

Самостоятельная работа проводится на тех же листочках, на которых выполнялся тест. На боковой доске работают два ученика. После выполнения работы листочки сдаются учителю на проверку, а учащиеся проверяют решенные задачи у двух учащихся, которые выполняли задания на боковых досках.

6. Подведение итогов урока. Проводится в виде фронтальной беседы. Учитель просит назвать учащихся вопросы и задания, которые у них вызвали затруднения и наоборот показались им несложными. С учетом работы в течение всего урока комментируются и оцениваются устные ответы учащихся.

7. Постановка домашнего задания.

Приложение 1.

Задания теста:

1 вариант.

1) Любой прямоугольник является:

а) ромбом; б) квадратом; в) параллелограммом; г) нет правильного ответа. 2) Закончите предложение:

Если в четырехугольнике диагонали перпендикулярны, то этот четырехугольник…

а) ромб; б) квадрат; в) прямоугольник; г) нет правильного ответа. 3) Закончите предложение: Ромб - это четырехугольник, в котором…

а) диагонали точкой пересечения делятся пополам и равны; б) диагонали взаимно перпендикулярны и точкой пересечения делятся пополам; в) противолежащие углы равны, а противолежащие стороны параллельны; г) нет правильного ответа

4). Если одна сторона параллелограмма равна 10 см, а другая - 20 см, то периметр его равен:

а) 10 см; б) 20 см; в) 30см; г) 60 см.

5). Если один угол параллелограмма равен 42°, то чему равны другие его углы:

а) 42° и 82°; б) 42°, 84°; в) 42°, 138°; г) 84°,138°.

6). Если диагональ параллелограмма образует с его сторонами углы 30° и 40°, то углы параллелограмма равны:

а) 60° и 80°; б) 70° и 10°; в) 70° и 110°.

2 вариант.

1). Любой ромб является:

а) квадратом; б) прямоугольником; в) параллелограммом; г) нет правильного ответа.

2).Если в параллелограмме диагонали перпендикулярны, то этот параллелограмм…

а) ромб; б) квадрат; в) прямоугольник; г) нет правильного ответа.

3). Прямоугольник - это четырехугольник, в котором:

а) противолежащие стороны параллельны, а диагонали равны; б) диагонали точкой пересечения делятся пополам и являются биссектрисами его углов; в) два угла прямые и две стороны равны; г) нет правильного ответа.

4). Чему равна сумма углов параллелограмма:

а) 180°; б) 90°; в) 360°; г) 720°.

4). Если стороны параллелограмма равны 3 см и 5 см, то какие это стороны

а) соседние; б) противоположные; в) любые.

5). Сумма двух углов параллелограмма равна 100°. Какие это углы:

а) соседние; б) противоположные; в) любые..