Семинар ДООМ Разработка урока по теме "Подобие прямоугольных треугольников"

План – конспект урока по геометрии в 9 классе.
Тема урока: Подобие прямоугольных треугольников.

Разработала Баканчикова Любовь Николаевна --Многогранники IDm071 00:10, 20 декабря 2009 (SAMT)

Цель урока: Показать применение признака подобия треугольников по двум углам к подобию прямоугольных треугольников. Вывести, опираясь на подобие прямоугольных треугольников, формулу для вычисления катета прямоугольного треугольника по его гипотенузе и проекции катета на гипотенузу. Проверить сформированность навыка решения задач по теме «Признаки подобия треугольников» и понятие среднего пропорционального (геометрического) чисел a и b.

Ход урока.

1. Проверка домашней работы.
Задачи № 35(2) и 18 два учащихся решают на доске.

Задача № 35


Дополнительные вопросы ученику:

1) Какие треугольники называются подобными?

2) Прочитать тот признак подобия треугольников, который был применен в задаче.

3) Дать определение среднего геометрического двух чисел.

Задача №18


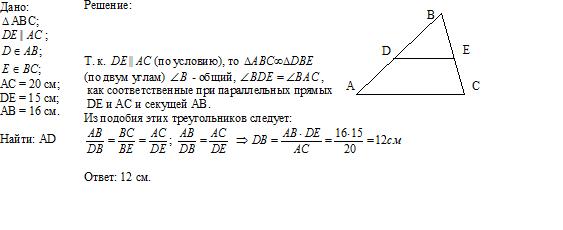
Пока ученики готовятся к ответу, класс работает с учителем.

1) Решить задачи устно по готовым рисункам. Закончить начатую запись и прочитать соответствующий признак подобия треугольников:

2) Найти средние пропорциональные чисел a и b, если:
а) a = 1; b = 25
б) a = 2; b = 3
в) a = 9; b = 16.
Замечание: прежде чем назвать ответ, ученик должен дать определение среднего пропорционального двух чисел.
Дополнительные вопросы:
1) По какому признаку подобны все равносторонние треугольники?
2) Когда будут подобны равнобедренные треугольники?

Оценка «5» ставится в том случае, если к ответу ученика учитель не сможет задать вопрос, который он бы не освятил во время объяснения. Если вопросы остались, и ученик верно ответил на них, учитель может задать дополнительный вопрос.

2. Изучение нового материала.

Учитель держит в руке модель прямоугольного треугольника.
Вопросы к классу:

1. Что у меня в руке? (прямоугольный треугольник).
2. Как называются стороны этого треугольника? (гипотенуза и катеты).

Учитель держит в руках модели двух прямоугольных треугольников.
Вопросы к классу:

1. Что у меня в руках? (прямоугольные треугольники).
2. Каким свойством обладают все прямоугольные треугольники? (у них один угол прямой).
3. А теперь хорошо подумали и ответили на вопрос, чего не хватает прямоугольным треугольникам для их подобия? (равенства одного из острых углов).
4. Тогда по какому признаку они будут подобны? (по двум углам).

Сформулируйте признак подобия прямоугольных треугольников, начиная со слова «Если»
Ученик: «Если острый угол одного прямоугольного треугольника соответственно равен острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники подобны»
Посмотрим, что по этому поводу написано в учебнике, откройте страницу 151.
«Для подобия двух прямоугольных треугольников достаточно, чтобы у них было по равному острому углу».
Обратите внимание, мысль одна: равенство острых углов, но излагали мы ее по-разному. Для объяснения выберите то, что вам по душе, на не забывайте о главном: равенство одного из острых углов.

3. Закрепление изученного материала
По рисункам, заранее заготовленным на доске закончить предложение:


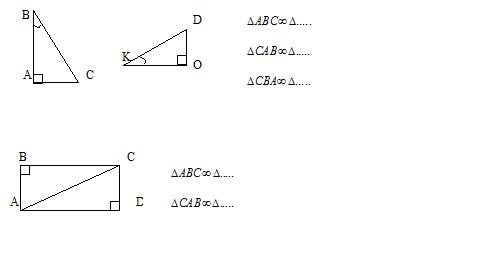
4. Изучение нового материала.
Учитель вызывает ученика к доске. Класс работает вместе с ним.
Учитель – ученику:


Вспомните, что такое средне пропорциональное двух чисел и сделайте вывод о том, как найти катет прямоугольного треугольника. (ученик выводит свое правило).
А теперь читаем этот вывод на странице 151.
"Катет прямоугольного треугольника есть средне пропорциональное между гипотенузой и проекцией этого катета на гипотенузу."Затем правило читается со словами «средне геометрическое».

5. Закрепление изученного материала.
На доске заранее заготовлена задача.
К доске с учебником выходит ученик. Он анализирует данные задачи, читает соответствующее правило и решает задачу.


6. Итог урока. Домашнее задание.

А сейчас мой традиционный вопрос классу: «Что, к тому, что мы уже знали по геометрии, добавилось сегодня на уроке?» Ученики отвечают:
1) Признак подобия прямоугольных треугольников.
2) Правило вычисления длины катета по гипотенузе и его проекции на гипотенузу.

Домашнее задание поможет вам закрепить этот материал.
Учить – страница 151.
Решать №39(1) №40
Повторить теорему Пифагора.