Семинар ДООМ Конспект урока Сумма углов треугольника

Холоденко Надежда Ивановна, IDm046

Тема: Сумма углов треугольника.

Цели урока: сформировать и доказать теорему о сумме углов треугольника, рассмотреть следствия из этой теоремы; формировать умение анализировать, обобщать, развивать математическую речь.

Ход урока.

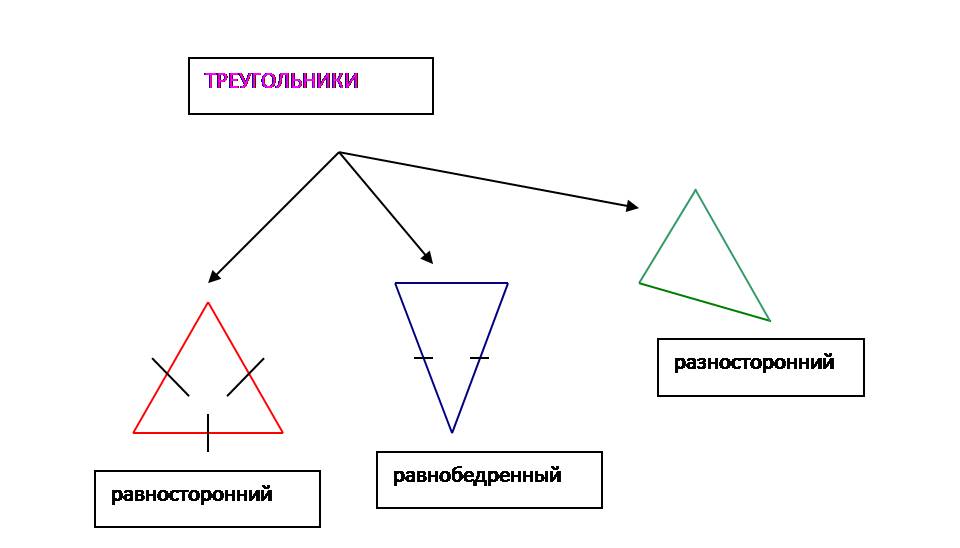
Устная работа. 1) Сегодня на уроке мы работаем с треугольником, одной из основных фигур геометрии. - Что такое треугольник? (Треугольник – фигура, образованная тремя точками, не лежащими на одной прямой, и отрезками, попарно соединяющими эти точки.) - Какие треугольники различают по сторонам? (Равносторонние, равнобедренные или разносторонние)

Сегодня мы узнаем, как классифицируют треугольники по углам. Давайте вспомним об углах. Составьте рассказ по теме «Угол». Можно использовать план: План. 1.) Угол – это фигура… 2.) Если…, то угол называют… 3.) Внутренний угол треугольника – это… (Угол – это фигура, образованная двумя лучами, выходящими из одной точки. Лучи называют сторонами угла, а точку – вершиной. Если величина угла 900 , то угол называют прямым, если угол меньше 900, то его называют острым. Угол больше 900, но меньше 1800 называют тупым. Развёрнутый угол равен 1800. Внутренний угол треугольника – угол, образованный его сторонами, вершина треугольника является вершина его угла. Значит, в треугольнике углы могут быть тупыми, острыми, прямыми.) Практическое задание: 1. Начертить угол: Тупой (I ряд), прямой (II ряд), острый (III ряд) 2. Дополнить рисунок до треугольника. Что для этого нужно сделать? (Взять по точке на сторонах угла и соединить их отрезками.) 3. Измерить транспортиром углы треугольников, изображённых в тетради и найти их сумму. Запишем некоторые результаты на доске. (1800, 1820, 1850, 1780) Что мы заметили? (все суммы близки к 1800) Докажем одну из важнейших теорем геометрии – теорему о сумме углов треугольника. Сумма углов треугольника равна 1800

Дано: треугольник АВС; ∟1, ∟2, ∟3 – внутренние углы. Доказать: ∟1 + ∟2 + ∟3 = 1800. Доказательство: 1.) Через вершину В проведём прямую параллельную АС. 2.) ∟5 = ∟3 (как внутренние, накрест лежащие при параллельных и секущей ВС) ∟1 = ∟4 (как внутренние, накрест лежащие при параллельных и секущей АВ) 3.) ∟4 + ∟2 + ∟5 =1800 (развёрнутый угол) 4.) ∟1 + ∟2 + ∟3 =1800 – ЧТД Запишем теорему и доказательство в тетрадь. (По желанию вызываем учащегося к доске, чтобы повторить доказательство теоремы) Из этой теоремы следует, что в любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой.

Полученные треугольники можно назвать (по углам): остроугольный, прямоугольный, тупоугольный. Если все три угла треугольника острые, то треугольник называется остроугольным. Если один из углов треугольника прямой, то треугольник называется прямоугольным. Если один из углов треугольника тупой, то треугольник называется тупоугольным. Устная работа: - Чему равен угол равностороннего треугольника? (600) (т.к. все три угла равны, т.е. 1800 : 3=600) - Чему равна сумма острых углов прямоугольного треугольника? (900) (1800 – 900 =900) -Чему равен острый угол прямоугольного равнобедренного треугольника? (450) - Почему в треугольнике не может быть два прямых (тупых) угла? (900 * 2 = 1800, т.е. на третий угол не остаётся ничего, а два тупых угла уже больше 1800) Ответы на поставленные вопросы вытекают (следуют) из теоремы, т.е. являются следствиями теоремы. Работа с учебником. № 223 (а, в), №228 (а, в) Задание на дом: стр.84 вопрос 1, № 223 (б, г), №228 (б, г), 226*