Семинар ДООМ:Элективный курс «Избранные вопросы по математике», 9 класс
Содержание[убрать] |
Пояснительная записка.
Курс «Избранные вопросы по математике» предназначен для учащихся 9 классов и ориентирован на углубленное изучение математики учащимися.
Углубленное изучение математики предусматривает формирование у учащихся устойчивого интереса к предмету, выявление и развитие математических способностей, ориентацию на профессию, существенным образом связанные с математикой, подготовку к обучению в вузе.
Для этого в программу включаются задачи, решаемые нестандартными методами, задачи прикладного характера. С помощью данного курса учащиеся могут углубить свои представления о математических понятиях, расширить кругозор, познакомившись с понятиями и фактами, которых нет в учебнике.
Данный курс является предметно-ориентированным.
Основные цели курса:
- повышение уровня общей математической подготовки;
- развитие логического мышления;
- развитие творческих и исследовательских способностей учащихся;
- духовное развитие и обогащение учащихся.
Структура программы содержит три раздела.
1.Уравнения, содержащие целую и дробные части числа.
Основная цель- рассмотрение основных способов решения уравнений ,задач и неравенств ,содержащих целую и дробную части числа, найти их рациональное решение.
2.Замечательные кривые.
Основная цель- систематизация и углубление знаний учащихся о свойствах известных замечательных кривых, применении кривых в технических расчетах.
3.Функции и графики.
Основная цель- рассмотрение построений графиков кусочно-линейных и кусочно-элементарных функций.
Основные задачи курса:
- обеспечить прочное и сознательное усвоение учащимися системы основных математических знаний и умений;
- сформировать навыки и умения решений уравнений и неравенств, содержащих целую и дробные части числа;
- познакомить учащихся с замечательными кривыми и способами их построения;
- способствовать формированию навыков построения функций без производной;
- сформировать представление о математике как об языке, описывающем закономерности реального мира.
Программа знакомит учащихся с элементами традиционной программы, изучаемых в 10-11 классах, и наряду с этим, с элементами углубленного изучения. Весь материал включает в себя информацию за пределами школьной программы.
Курс рассчитан на 34 часа в год или 1 час в неделю.
Срок реализации данной программы один учебный год.
В результате изучения курса учащиеся должны
знать:
- свойства целой и дробной части числа;
- свойства графиков основных замечательных кривых;
уметь:
- решать уравнения, содержащие целую и дробную части числа;
- решать уравнения, содержащие композиции из целой и дробной части числа;
- решать неравенства первой и второй степени, содержащие целую часть числа;
- строить графики функций, содержащие целую и дробную части числа;
- строить замечательные кривые;
- строить графики кусочно-линейных функций без производной.
Изучение каждой темы курса начинается с лекции. Далее учащиеся с помощью учителя решают задачи по данной теме (семинары) и в конце занятия получают домашнее задание. После изучения каждого раздела проводится зачет.
Содержание курса предполагает самостоятельную подготовку учащихся: работу с разными источниками информации (справочные пособия, учебная литература, Интернет и т.д.). Содержание каждого раздела курса включает в себя самостоятельную (индивидуальную, групповую, коллективную) работу учащихся, что позволяет формировать навыки коллективной работы, работы в группах разного уровня , развивать коммуникативные способности.
Курс «Избранные вопросы по математике», предназначенный для учащихся 9 классов, представляется особенно актуальным, так как вооружает учащихся знаниями по темам: «Уравнения, содержащие целую и дробные части числа», «Замечательные кривые», «Функции и графики». Эти математические знания необходимы для дальнейшего изучения математики.
Углубленное изучение математики предполагает наличие у учащихся устойчивого интереса к математике и намерение выбрать после окончания школы связанную с ней профессию. Обучение на этом этапе должно обеспечить подготовку к поступлению в вуз и продолжению образования, а также к профессиональной деятельности, требующей достаточно высокой математической культуры.
Результатом изучения курса должно стать умение применять изученные методы к самостоятельному решению задач. Эта цель достигается формированием на более высоком уровне умений и навыков решения задач повышенной сложности, по сравнению с обязательным уровнем.
Формы проведения итогов реализации дополнительной образовательной программы: учебно-исследовательские конференции школьного и городского уровня.
Содержание курса
Содержание предлагаемого курса включает в себя три раздела:
- Уравнения, содержащие целую и дробные части числа.
- Замечательные кривые.
- Функции и графики.
Главное назначение первого раздела – изучение основных способов решения уравнений, задач и неравенств, содержащих целую и дробную части числа.
Второй раздел включает в себя изучение свойств известных замечательных кривых на основе имеющихся знаний и организации самостоятельной математической деятельности учащихся.
В третьем разделе рассматриваются построения графиков кусочно-линейных и кусочно-элементарных функций без производной.
Содержание курса включает в себя изучение следующих вопросов:
Раздел 1. Уравнения, содержащие целую и дробную части числа
Тема 1. Целая часть числа.
Свойство целой части числа. Функция у = [ х ]. График и ее свойства.
В лекционной форме вводится определение целой части числа. Выводятся свойства целой части числа. Вводится функция у = [ х ]. Рассматривается ее график и свойства.
Тема 2. Простейшие уравнения, содержащие целую часть числа.
Алгоритмы решения уравнений, содержащих целую часть числа.
Занятие проводится в форме семинара. Учащиеся знакомятся с основными алгоритмами решения уравнений, содержащих целую часть числа.
Тема 3. Дробная часть числа.
Свойство дробной части числа. Функция у = { х }. График и ее свойства.
В лекционной форме вводится определение дробной части числа. Выводятся свойства дробной части числа. Вводится функция у = { х }. Рассматривается ее график и свойства.
Тема 4. Простейшие уравнения, содержащие дробную часть числа.
Алгоритмы решения уравнений, содержащих дробную часть числа.
Занятие проводится в форме семинара. Учащиеся знакомятся с основными алгоритмами решения уравнений, содержащих дробную часть числа.
Тема 5. Композиции из целой и дробной частей числа
Свойство композиции из целой и дробной частей числа.
Уравнения, содержащие композиции из целой и дробной частей числа.
Системы уравнений ,содержащие композиции из целой и дробной частей числа .
Занятие проводится в форме практикума. Учащиеся знакомятся с решениями уравнений , содержащих целую часть числа.
Тема 6. Простейшие неравенства первой степени , содержащие целую и дробную часть числа.
В лекционной форме выводится решение основных неравенств с целой и дробной частью числа.
Тема 7.Решение уравнений и неравенств с модулем.
Решение уравнений с модулем. Решение неравенств с модулем.
Занятие проводится в форме практикума. Учащиеся знакомятся с решениями уравнений и неравенств , содержащих целую часть числа.
Тема 8. Построение графиков функций, содержащих целую и дробную части числа.
Построение графиков функций, содержащих целую и дробную части числа. Графическое решение уравнений.
Раздел 2. Замечательные кривые.
Тема 1. Эллипс. Гипербола. Парабола.
Эллипс. Определение. Фокус эллипса. Построение эллипса.
Гипербола. Определение. Фокус гиперболы. Построение гиперболы.
Парабола. Определение. Построение параболы.
Общее свойство эллипса, гиперболы, параболы.
Тема 2. Циклоида.
Спираль Архимеда.
Циклоида. Построение циклоиды. Парадокс Аристотеля. Свойство циклоиды. Касательная и нормаль к циклоиде.
Геометрическое определение циклоиды. Ее площадь.
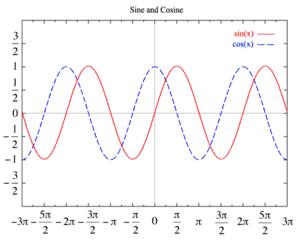
Синусоида. Построение синусоиды.
Тема 3. Родственники циклоиды.
Трохоида. Построение трохоиды.
Эпициклоиды. Построение эпициклоиды
Эпициклоиды с бесконечным множеством арок.
Тема 4.Кардиоида.
Построение кардиоиды. Замечательное свойство кардиоиды.
Улитка Паскаля.
Конхоида. Построение конхоиды.
Гипоциклоиды и их различные виды. Астроида.
Тема 5. Применение свойств кривых в науке и технике.
Циклоидальный маятник. Задача о бранстохроне.
Оптическая задача Ферма.
Применение свойств кривых в науке и технике. Лемниската.
Занятия проводятся в форме защиты проектов, самостоятельного исследования учащихся.
Раздел 3. Графики функций.
Тема. Построение графиков функции (без производной).
Построение графиков функции (без производной). Графики многочленов. Графики дробно-рациональных функций.
В лекционной форме вводятся этапы построения графиков функций и новые понятия, необходимые для более полного построения графиков многочленов высших степеней и графиков дробно-рациональных функций. Важно научить учащихся строить графики сложных функций без аппарата производной.
Методическое обеспечение программы.
В рамках изучения данного курса целесообразно использовать различные формы организации деятельности учащихся. Занятия можно проводить в форме лекций, семинаров, практикумов по решению задач, защиты проектов. Учащиеся самостоятельно, в малых группах, в сотрудничестве с учителем выполняют различные задания в соответствии со своими познавательными возможностями.
Значительное внимание можно уделить обсуждению результатов коллективных и индивидуальных исследований, разнообразных творческих заданий, защиты проектов.
Особое внимание следует уделять развитию умений учащихся самостоятельно приобретать новые математически знания.
Раздел 2. Замечательные кривые.
Основным видом профильного обучения является допрофессиональная познавательная деятельность учащихся, формирующая у них творческие качества личности и ключевые компетентности. Метод проектов эффективно реализует содержание и идею профильного обучения.
В основе проектного обучения лежит самостоятельное конструирование своих знаний и процесса их пополнения, умение ориентироваться в информационном потоке, организация индивидуальной и коллективной учебной деятельности.
Для обучения на основе проектного метода необходимы следующие этапы:
- наличие значимой проблемы, решаемой с помощью интеграционных знаний,
- практической и теоретической значимости полученного результата,
- структурирование этапов выполнения проекта,
- применение в проектировании опыта исследовательской творческой учебной деятельности,
- самостоятельная деятельность учащихся,
- выбор формы презентации полученного результата,
- рефлексивная оценка полученного результата.
Замечательные геометрические объекты – кривые линии привлекают внимание не только изяществом своей формы, но и многими удивительными свойствами.
Возможные проекты в рамках данного курса:
1. Как построить эллипс, параболу и гиперболу с помощью веревки?
2. Применение свойств эллипса, гиперболы, параболы в технике.
3. Составление каталога замечательных кривых.
5. Общее свойство параболы, эллипса, гиперболы.
6. Директриса- это директор школы?
7. Виды и свойства спиралей.
8. Циклоида и ее свойства.
9. Спутница циклоиды-синусоида.
10. Родственники циклоиды.
11. Математический цветник.
12. Применение свойств циклоиды в технике.
13. Прменение свойств кардиоиды в технике.
14. Как быстрее скатиться с горы? (Задача о брахистохроне)
15. Применеие свойств кривых в науке и технике.
Лекционный материал
Тема 1. Эллипс. Гипербола. Парабола.
Эллипс. Определение. Фокус эллипса. Построение эллипса.
Гипербола. Определение. Фокус гиперболы. Построение гиперболы.
Парабола. Определение. Построение параболы.
Общее свойство эллипса, гиперболы, параболы.
Эллипс— множество точек плоскости, для которых сумма расстояний от двух данных точек F1 и F2 (называемых фокусами) постоянна, то есть | F1M | + | F2M | = 2a. Окружность является частным случаем эллипса. Наряду с гиперболой и параболой , эллипс является коническим сечением. Эллипс также можно описать как пересечение плоскости и кругового цилиндра или как ортогональную проекцию окружности на плоскость.
Катящаяся окружность рисует циклоиду.
Циклоида определяется кинематически как траектория фиксированной точки производящей окружности радиуса r, катящейся без скольжения по прямой.
Свойства
- Циклоида — периодическая функция по оси абсцисс, с периодом 2πr. За границы периода удобно принять особые точки (точки возврата) вида t = 2πk, где k — произвольное целое число.
- Для проведения касательной к циклоиде в произвольной её точке A достаточно соединить эту точку с верхней точкой производящей окружности. Соединив A с нижней точкой производящей окружности, мы получим нормаль.
- Длина арки циклоиды равна 8r. Это свойство открыл Кристофер Рен (1658).
- Площадь под каждой аркой циклоиды втрое больше, чем площадь порождающего круга. Торричелли уверяет, что этот факт был открыт Галилеем.
- Радиус кривизны у первой арки циклоиды равен .
- «Перевёрнутая» циклоида является кривой скорейшего спуска (брахистохроной). Более того, она имеет также свойство таутохронности: тяжёлое тело, помещённое в любую точку арки циклоиды, достигает горизонтали за одно и то же время.
- Период колебаний материальной точки, скользящей по перевёрнутой циклоиде, не зависит от амплитуды, этот факт был использован Гюйгенсом для создания точных механических часов.
- Эволюта циклоиды является циклоидой, конгруэнтной исходной, а именно — параллельно сдвинутой так, что вершины переходят в «острия».
- Детали машин, которые совершают одновременно равномерное вращательное и поступательное движение, описывают циклоидальные кривые (циклоида, эпициклоида, гипоциклоида, трохоида, астроида) (ср. построение лемнискаты Бернулли).
Первым из учёных обратил внимание на циклоиду Николай Кузанский в XV веке, но серьёзное исследование этой кривой началось только в XVII веке. Название циклоида придумал Галилей (во Франции эту кривую сначала называли рулеттой).
Содержательное исследование циклоиды провёл современник Галилея Мерсенн. Паскаль писал о циклоиде:
Рулетта является линией столь обычной, что после прямой и окружности нет более часто встречающейся линии; она так часто вычерчивается перед глазами каждого, что надо удивляться тому, как не рассмотрели её древние… ибо это не что иное, как путь, описываемый в воздухе гвоздём колеса.
Новая кривая быстро завоевала популярность и подверглась глубокому анализу, в котором участвовали Декарт, Ферма, Ньютон, Лейбниц, братья Бернулли и другие корифеи науки XVII—XVIII веков. На циклоиде активно оттачивались методы появившегося в те годы математического анализа.
Синусоида — плоская кривая, задаваемая уравнением y = a + bsin(cx + d). График функций синус и косинус представляет собой синусоиду.
Лекционный материал по теме 3. Родственники циклоиды.
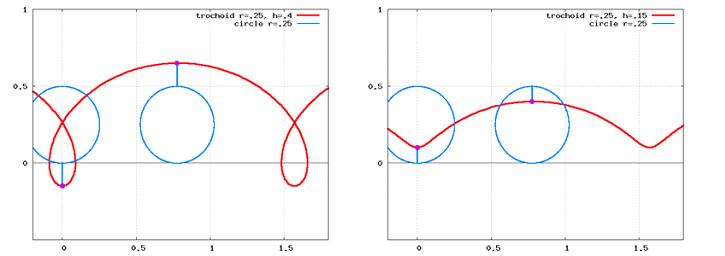
Трохоида представляет собой траекторию точки, жёстко связанной с окружностью радиуса r, катящейся без скольжения по прямой (в приведённом примере такой прямой является горизонтальная ось координат). Расстояние точки от центра окружности — h.
Если h = r трохоида переходит в циклоиду.
При h > r трохоиду называют удлинённой циклоидой, а при h < r — укороченной циклоидой.
Удлинённая циклоида Укороченная циклоида
Практическая реализация в электровакуумных приборах - трохотронах, в которых электроны перемещаются по трохоидальным кривым.
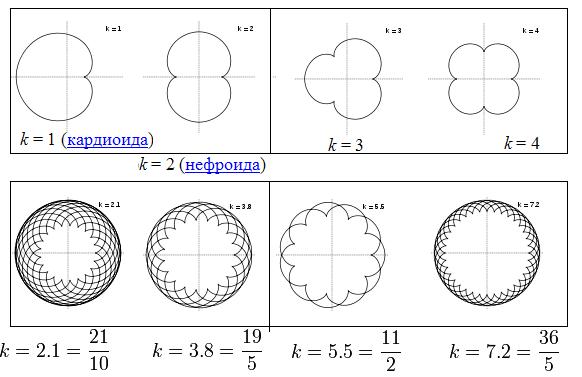
Эпициклоида — плоская кривая, образуемая фиксированной точкой окружности, катящейся по другой окружности.
Эпициклоиды при разных значениях параметра k:
Лекционный материал по теме 4.Кардиоида.
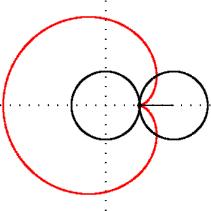
Кардиоида— плоская линия, которая описывается фиксированной точкой окружности, катящейся по неподвижной окружности с таким же радиусом. Получила своё название из за схожести своих очертаний со стилизованным изображением сердца.
Кардиоида является частным случаем улитки Паскаля, эпициклоиды и синусоидальной спирали.
Материал из ВИКИПЕДИИ