Семинар ДООМ "Можно ли не ломая проволоки изготовить каркас куба?"

Цель занятия:

ввести понятие уникурсального (эйлерова) графа;

выявить, проведя математическое исследование, закономерности между возможностью нарисовать граф одним росчерком и степенями вершин графа;

сформировать умения определять является ли граф уникурсальным.

Ход урока:

1. Организационный момент

Сегодня на уроке нам предстоит ответить на вопрос «Можно ли не ломая про-волоки изготовить каркас куба?».

2. Историческая справка (5 мин)

Теория графов один из немногих разделов математики, год рождения которого можно указать достаточно точно. Первая работа, положившая начало этой теории, опубликована в 1736 г (хотя сам термин «граф» появился несколько позднее). А дело было так. В XVIII веке на реке Прегель, протекавшей по городу Кенигсберг (ныне Калининград), было построено 7 мостов. Эти мосты связывали берега с двумя островами, расположенными в черте города (рис. 1). Излюбленным занятием жителей города в воскресные дни были прогулки по набережной и мостам. Однажды один из жителей города заинтересовался, можно ли пройти по всем мостам так, чтобы на каждом из них побывать лишь один раз и вернуться к тому месту, откуда начал прогулку. Одна-ко найти решение этой задачи он не смог, более того, ее не удалось решить никому из жителей города.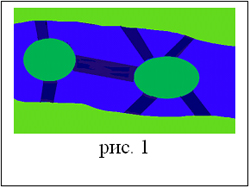 Задачей заинтересовались математики разных стран, и вот в 1736 году было найдено решение. Оно принадлежало известному швейцарскому ученому Леонарду Эйлеру, который почти всю жизнь проработал и Петербургской Академии наук, где добился блестящих успехов в математике, физике и астрономии. Решив эту задачу о кенигсбергских мостах, он указал общий метод решения аналогичных задач. Идеи, использованные Эйлером, явились фундаментом теории, называемой теперь теорией графов.

3. Актуализация знаний (3–5 мин)

Предложить ученикам ответить на следующие вопросы по ранее рассмотренным темам:

1 Что называют графом?

2 Кто и в каком году впервые ввел термин «граф»?

3 Что называют ребром графа, вершиной графа?

4 Что называют степенью вершины графа?

5 Какие вершины графа называют четными, какие нечетными?

4. Математическое исследование (10 мин)

Класс делится на группы по 4–5 человек. Каждая группа получает задание (Приложение №1). Учитель принимает активное участие в процессе поиска ответов на по-ставленные вопросы, помогает группам, координирует работу групп и, если возника-ют затруднения у некоторых групп, привлекает все группы к совместному обсужде-нию полученных результатов.

5. Обсуждение полученных результатов (7–10 мин)

a) Каждая группа делится полученными результатами в процессе математическо-го исследования.

b) Выводы обсуждаются под руководством учителя по каждому пункту работы.

c) Определения и выводы записываются в тетради.

В тетради:

ОПРЕДЕЛЕНИЕ: Граф, который можно нарисовать, не отрывая карандаша от бумаги и проводя каждое ребро один раз, называется эйлеровым или уникур-сальным.

ВЫВОД 1: Если все вершины графа четные, то его можно начертить одним росчерком (не отрывая карандаша от бумаги), при этом движение можно начать в любой вершине и закончить его в той же вершине.

ВЫВОД 2: Если граф имеет только две нечетные вершины, то его можно на-чертить одним росчерком (не отрывая карандаша от бумаги), при этом движение на-чать нужно в одной нечетной вершине, а закончить в другой.

ВЫВОД 3: Граф с более чес двумя нечетными вершинами нельзя начертить од-ним росчерком.

6. Решение задач по теме (3 мин)

Рассмотрим ответ на вопрос нашего занятия: «Дан кусок проволоки 120 см. Можно ли не ломая проволоки изготовить каркас куба с ребром 10 см?» 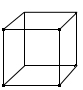Этот вопрос можно сформулировать по-другому: Можно ли нарисовать граф, состоящий из вершин и ребер куба, одним росчерком? Является ли данный граф уникурсальным?

Решение: У куба (графа) 8 вершин и 12 ребер. Т.к. 12.10=120 см, то длины про-волоки хватит на каркас куба, но степень каждой вершины нечетная (третья). Значит, граф не является уникурсальным. Ответ на наш вопрос – нельзя таким образом изготовить каркас куба.

Решение задач по карточке заданий (5 мин)

Задача 1. Граф, соответствующий задаче о кенигсбергских мостах (все вершины нечетные) Уберем один мост, как показано на рисунке, и получим все четные вершины, кроме двух. Значит, граф уникурсальный и можно обойти все ребра по одному разу, начав движение в одной нечетной вершине и закончив в другой нечетной вершине. Добавим один мост, как показано на рисунке. Рассуждения аналогичные.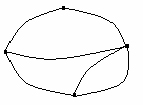

Задача 2. Уникурсальные фигуры:

а, б, в, г, ж, к, м, р, т – все вершины четные, л, о, с – только две вершины нечетные.

7. Итоги урока

Вопрос 1 Какой граф называют эйлеровым?

Вопрос 2 Дайте другое название эйлерова графа.

Вопрос 3 Можно ли нарисовать граф с четными вершинами одним росчерком?

Вопрос 4 Является ли граф с двумя нечерными вершинами уникурсальным?

Вопрос 5 Является ли граф с тремя и более нечерными вершинами уникурсальным?

Вопрос 6 В каком случае можно нарисовать граф одним росчерком, начиная и заканчивая движение в одной вершине (в разных вершинах)?

8. Домашнее задание:

1. Задача №2 (д, е, ж, з)

2. Если граф нельзя нарисовать одним росчерком, то какое минимальное число росчерков существует, которыми этот граф можно нарисовать?

3. Рассмотреть на примере кенигсбергских мостов, куба и графа на рисунке