Семинар ДООМ "Математический КВН"

Соревнования между учащимися 6-7 классов.

Цель:

Образовательная:- рассмотреть решение логических задач и головоломок с помощью теории графов,

- расширение математического кругозора,

- формирование графических и логических умений.

Воспитательная:

- предоставить возможность проявить себя детям с разным уровнем подготовки , разной скоростью мышления,

- выработать умение работать в команде,

- выявить лучшую команду.

Развивающая:

- развивать умение обобщать, систематизировать на основе сравнения , делать вывод,

- развивать познавательный интерес к математике,

- пробуждение творческой активности учащихся,

- интеллектуальное развитие учащихся.

Методы и приемы:

Эстафета, программированный опрос, экспресс - ответы.

Форма организации труда:

Групповая и индивидуальная

Участники: 4 команды 6-7 классов по 10 человек в каждой, болельщики .

Судьи: участники 11 классов, учителя школы.

Оборудование: магнитная доска, раздаточный наглядный материал ,сигнальные карточки, таблицы.

Структура

1 Вступление. Представление жюри. Жеребьевка. Правила игры.

2 Визитка команды( девиз, название, эмблема, приветствие жюри и соперников.

3 Конкурс логиков (Груповое решение задачи)

4 Конкурс художников (Командное решение задания)

5 Конкурс эрудитов (Экспресс-ответ)

6 Конкурс мусорщиков (Тестовое задание с выбором ответа)

7 Конкурс поисковиков (Командное решение задания)

8 Конкурс вычислителей (Эстафета по командам)

9 Конкурс капитанов

10 Выступления болельщиков с математическими номерами.

11 Подведение итогов.Награждение.

В перерывах между конкурсами конкурсы болельщиков - итоги предыдущих конкурсов.

Время проведения 1,5 часа.

Правила КВН.

1. Задания подбираются разного уровня трудности, среди них встречаются и олимпиадные задачи.

2. Критерии оценивания решения заданий

3 балла - правильное решение

2 балла - неполный ответ

1 балл - частичный ответ

3. При решении заданий нельзя общаться с болельщиками.

4. Командам одновременно предлагается ряд заданий и сообщается время, отведенное на их решение.

5. По окончании решения заданий каждая команда рассказывает или показывает свое решение.

6. Если команда не справляется с решением задач, то им помогают болельщики.

7. Выигрывает та команда, которая наберет в сумме наибольшее количество баллов.

8. За досрочные ответы баллы не добавляются.

9. Если команды набрали равное количество баллов, а победитель должен быть обязательно определен, то командам предлагаются дополнительные задачи, количество которых определяет жюри.

Конкурс логиков.

Задание1.

У марсиан бывает произвольное число рук. Однажды все марсиане взялись за руки так, что свободных рук не осталось. Докажите, что количество марсиан с нечетным числом рук четно.

Задание 2.

Докажите, что число перекрестков любого города, в которых встречается нечетное число улиц- четно.

Задание 3.

Докажите, что число зрителей, пришедших на стадион смотреть футбольный матч и имеющих нечетное число знакомых (среди того же множества зрителей) четно.

Задание 4.

Докажите, что число людей, когда-либо живших на Земле и сделавших нечетное число рукопожатий, четно.

Конкурс художников.

Задание. Построить граф с вершинами в точках.

А.Б.

1.( 0 , 8 )

2.( 3 , 9 )

3.( 1 , 12 )

4.( 3 ,11 )

5.( 7, 12 )

6.( 9 , 10 )

7.( 5 , 7 )

8.( 7,7 )

9.( 9 ,5 )

10.(12 , 6 )

11.( 9 , 2 )

12.( 7 ,1 )

13. ( 2, 1 )

14.( 4 , ІІ )

15.( 1 , 3 )

16.( 1 , 7 )

17. ( 3 , 8 )

18.( 0 , 8 )

ГЛАЗ ( 5 , 10 )

В.Г.

1.( 10 ,11 )

2..( 9 , 12 )

3.( 8,12 )

4.( 6 ,11 )

5.( 3 , 8 )

6.( 2 ,4 )

7.( 0 , 1 )

8. ( 2 , 1 )

9.( 3, 3 )

10.( 4 , 4 )

11.( 8 , 6 )

12.( 7 , 6 )

13.( 8 , 7 )

14.( 9 , 9 )

15.( 8 , 10 )

16.( 9 , 11 )

17. ( 10, 11)

Глаз ?

Конкурс эрудитов.

Задание. Закончить математическое предложение или ответить на вопрос. Каждой команде выделяется только 1 минута для ответа на все вопросы. Требуется ответить на все вопросы правильно.

Эспресс - конкурс .

А.Вопросы.

1. Графом называется …?

2.Какое число нечетное 5 или 17?

3. Буквы Л и О уникурсальны?

4. Сколько вершин графа соединяет одно ребро?

5. Является ли графом схема автомобильных дорог?

6.Сколько ребер имеет нулевой граф с 5 вершинами?

7.Граф имеет 6 вершин. Сколько ребер выходит из каждой вершины?

Б.Вопросы.

1. Ребром графа называется…?

2. Какое число нечетное 6 или 12?

3. Уникурсальная фигура это …?

4. Буквы О и Д уникурсальны - …

5.Является ли графом схема метрополитена?

6.Сколько ребер имеет нулевой граф с 4 вершинами?

7.Граф имеет 8 вершин. Сколько ребер выходит из каждой вершины?

В. Вопросы.

1. Вершиной графа называется?

2. Какое число четное 8 или 7?

3. Буквы М и Ш уникурсальны?

4. Является ли графом географическая карта?

5.Сколько ребер имеет нулевой граф с 7 вершинами?

6.Какая фигура не уникурсальна?

7.Граф имеет 6 вершин. Сколько ребер выходит из каждой вершины?

Г.Вопросы.

1. Степенью вершины графа называется?

2. Какое число четное 3 или 10?

3. Буквы Т и Ш уникурсальны?

4. Является ли графом множество городов и соединяющие их дороги?

5.Сколько ребер имеет нулевой граф с 15 вершинами?

6. Каким числом всегда является сумма степеней вершин графа?

7.Граф имеет 11 вершин. Сколько ребер выходит из каждой вершины?

Конкурс мусорщиков.

Задание.

Убери лишнее слово. Объясни почему. Командам выдаются карточки со словами.

А.

Вершина

Цепь

Ребро

Велосипед

Ответ: велосипед

Б.

Прямоугольник.

Квадрат.

Треугольник.

Трапеция.

Ответ: Треугольник

В.

Дерево

Лес

Граф

Ветви

Ответ: ветви

Г.

О Е Ш Т

Ответ: О

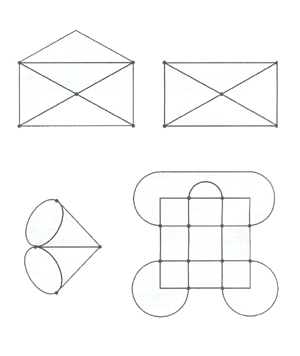
Конкурс поисковиков.

Найти уникурсальные фигуры?

Конкурс вычислителей.

Задание. Вычислить и подняться по лесенке. Игра в форме эстафеты. На доске висят задачи плакатах. Участники – команды решают задачи по одному цепочкой. К доске выходят одновременно по одному человеку от каждой команды. Порядок выхода к доске определяет капитан , который сам не участвует в эстафете. Каждый участник обязательно записывает ответ на соответствующей лесенке. Выигрывает та команда, которая поднимется на последнюю лесенку, получив правильный ответ.

1.Николай, Петр, Алексей, Александр, Михаил при встрече обменялись рукопожатиями (каждый пожал руку каждому по одному разу). Сколько всего рукопожатий было сделано?

2.Футбольный мяч представляет собой многогранник с 32 гранями , 20 из которых – белые правильные шестиугольники, а 12- черные правильные пятиугольники. Сколько вершин у такого многогранника?

3.У Пети есть моток жесткой проволоки длиной 12 дм. На какое наименьшее число кусков его надо разрезать, чтобы собрать каркас куба с ребром 1 дм ?

4.В государстве 100 городов, и из каждого из них выходит по 4 дороги. Сколько всего дорог в государстве?

5.В обеденный перерыв члены строительной бригады разговорились о том, кто сколько газет читает. Выяснилось, что каждый выписывает и читает две и только две газеты, каждую газету читает пять человек, и любая комбинация газет читается одним человеком. Сколько различных газет выписывают члены бригады?

Конкурс капитанов.

Задание. Решить логическую задачу с помощью графов.

Необходимо составить фрагмент расписания для одного дня с учетом следующих обстоятельств:

1.учитель истории может дать либо первый, либо второй, либо третий уроки, но только один урок;

2.учитель литературы может дать один, либо второй, либо третий урок;

3.математик готов дать либо только первый, либо только второй уроки;

4.преподаватель физкультуры согласен дать только последний урок.

Сколько и каких вариантов расписания, удовлетворяющего всем вышеперечисленным условиям одновременно, может составить завуч?

Вопросы болельщикам.

1.Собрать букву Т из четырех элементов.

2.Сколько нулей в произведении от 1 до 50 ?

3.Какой цифрой оканчивается произведение 19•21•23•25•27•29•31.

Ответ: 5

4.Придумать фигуру человека , состоящую из геометрических фигур.

5.Какое двухзначное число при отражении в зеркале увеличится в 4.5 РАЗА?

Ответ:18•4,5 = 81

6.Сколько получится , если разделить полсотни на половину ?

Ответ:100

7.Найти число, равное утроенной сумме своих цифр.

Ответ: 2+7=9 , 9•3 = 27

8.Сколько всего трехзначных чисел?

Ответ: 900.

9.В ящике 70 груш двух сортов. Сколько надо взять груш не глядя, чтобы среди них оказались две груши одного сорта?

Ответ: 3

10.Сколько сейчас времени , если оставшаяся часть суток в 3 раза больше , чем пройденная?

Ответ: 6 часов.

11.25•5•2

Ответ: 250

12.87+21+13+79

Ответ: 250

13. Тройка лошадей проскакала 90 км. Сколько километров проскакала каждая лошадь?

Ответ: 200.

14.Найти два в квадрате, три в квадрате, угол в квадрате.

15.Горело 5 свечей, две погасли. Сколько свечей осталось?

16.Назовите самое большое число?

17.Что легче: килограмм пуха или килограмм железа?

18, Сколько бегемотов может увезти пятитонная машина, если вес одного бегемота 1500 кг ?

19. Один человек купил трех коз и заплатил 3 рубля. Спрашивается: по чем каждая коза пошла ?