Семинар ДООМ "Математический детектив"

Участник:Шишканова Наталья Алексеевна 018 Уважаемые коллеги! Хочу познакомить Вас с интересным и полезным учебным изданием. Автор: Мадер В.В. Математический детектив: Кн. для учащихся. - М.: Просвещение, 1992. Автор в занимательной форме знакомит читателя с методами решений логических задач. В первой главе рассматривается графический метод, во второй – табличный, в третьей главе показано, как решать логические задачи с помощью диаграмм Эйлера-Венна. Главы объединены занимательным сюжетом. Книга доступна учащимся, начиная с шестого класса. Предлагаю несколько историй из этой книги. История с отчетом о соревнованиях. Это дело возникло на соревнованиях по лёгкой атлетике. Наши ребята заняли первые четыре места. Но когда девочки стали вспоминать, как эти места распределились между победителями, то мнения разошлись. Было высказано три мнения. Даша сказала, что Андрей был первым, а Володя - вторым. Галя утверждала, что Андрей был вторым, а Борис – третьим. Лена же была убеждена, что Борис был четвертым, а Сергей – вторым. Холмс сказал, что эти утверждения противоречат друг другу. Тогда девочки обратились к Асе, которая была судьей на этих соревнованиях и поэтому хорошо помнила, как распределились места. Ася сказала, что каждая их трёх девочек сделала одно правильное и одно неправильное заявление. После этого Холмс помог девочкам восстановить истину. Он начал с того, что сделал рисунок.

«На этом рисунке, - сказал Холмс,— мнения всех трёх девочек изображены графически. Даша сказала, что Андрей был первым, а Володя – вторым. Поэтому я провел одну жирную линию между кружочками А и 1 и другую — между кружочками В и 2. Мнение Гали я отметил параллельными линиями, а мнение Лены — обычными линиями.

Ася сказала, что каждая девочка сделала только одно правильное заявление. Значит, из каждой пары одинаковых линий — жирных линий, параллельных линий и обычных линий — надо оставить только по одному компоненту пары. Начнём с жирных линий. Возможен только один из двух случаев: либо истинно только A l, либо истинно только В2 (т. е. либо Андрей занял первое место, а Володя второе место не занял, либо, наоборот, Володя занял второе место, но Андрей первое место не занял).

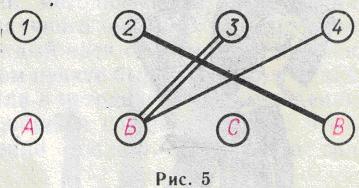
Допустим, что истинно В2, а A1 ложно. Так как A1 ложно, то линию A1 надо стереть. Далее, так как В2 истинно, то, кроме Володи, второе место никто занять не мог. Поэтому надо стереть А2 и С2. После этого получится рисунок 5.

От каждой пары одинаковых линий осталось по одной. Мы из каждой пары стерли тот компонент, который был ложным. Значит, все оставшиеся компоненты должны быть истинными (так как в каждой паре было ровно пo одному правильному заявлению). Но это невозможно, так как Борис не мог одновременно занять третье и четвертое место. Значит, допущение неверно.

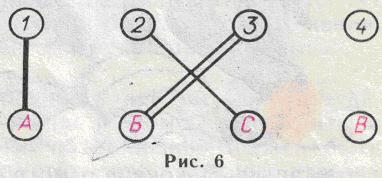
Рассмотрим теперь второй случай. Вернемся снова к рисунку 4. допустим, что A1 истинно, а В2 ложно. Значит, В2 надо стереть. Далее, так как A1 истинно, то А2 ложно (Андрей не мог занять сразу первое и второе места). Значит, стираем А2. Но если А2 ложно, то второй компонент этой пары Б3 должен быть истинным. А если Б3 истинно, то Б4 ложно. Значит, стираем Б4. После этого получится правильный рисунок(рис.6)

Теперь легко записать ответ: А1, С2, Б3, В4.»

История с амфорой

Это дело возникло летом, когда Холмс отдыхал в Крыму. Он тогда часто бывал на археологических раскопках и помогал рабочим. Однажды он сам откопал старинный сосуд — амфору. Осмотрев эту амфору, археологи высказали ряд предположений. Один сказал, что амфора изготовлена финикийцами в V веке. Второй сказал, что амфора изготовлена греками в III веке. А третий сказал, что амфора не греческая, а изготовлена в IV веке. После этого амфору долго рассматривал главный специалист. Он взял лупу и прочитал все надписи. Закончив осмотр, он сказал, что каждый из археологов был прав только наполовину: в каждом из трех предположений одно утверждение истинно, а одно ложно. Наступила пауза. Все ждали, что главный специалист подведет итог и скажет, когда и кем эта амфора была изготовлена. Но вместо этого главный специалист сказал: «Окончательный вывод вы можете сделать сами». Тогда Холмс сказал: «Вы правы, вывод совершенно очевиден: амфора изготовлена финикийцами в III веке».

Археологи удивились: им было непонятно, как Холмс пришел к такому выводу. Поэтому Холмсу пришлось, рассказать о том, как он рассуждал.

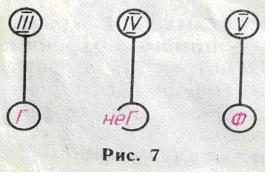
Как всегда, Холмс начал с рисунка (рис. 7).

Затем Холмс стал рассуждать следующим образом. Возможны только два случая: либо истинно Г, либо истинно не Г.

Рассмотрим первый случай. Допустим, что истинно Г. Тогда не Г ложно. А если не Г ложно, то второй компонент этой пары должен быть истинным. Значит, истинно IV. Если же IV истинно, то V ложно (в самом деле, если сосуд изготовлен в IV веке, то он не мог быть изготовленным в V веке). А если V ложно, то второй компонент этой пары истинный, т. е. истинно Ф. Мы допустили, что истинно Г, и пришли к выводу, что истинно Ф. Но сосуд не может быть одновременно и греческим и финикийским. Значит, наше допущение неверно.

Рассмотрим теперь второй случай. Допустим, что не Г истинно. Но если не Г истинно, то Г ложно. А если Г ложно, то второй компонент этой пары должен быть истинным. Значит, истинно III. Если же III истинно, то очевидно, V ложно. Но если V ложно, то второй компонент этой пары истинный. Значит, истинно Ф. Таким образом, получилось, что истинно Ф III. А это значит, что амфора была изготовлена финикийцами в III веке.

Странный приказ

Эта история произошла осенью после начала учебных занятий. Холмс как-то зашел в учительскую и на доске объявлений увидел приказ директора, в котором говорилось о создании методического объединения учителей, преподающих предметы естественнонаучного цикла. В этом приказе было три пункта. В первом говорилось, что каждый член объединения должен быть специалистом по двум предметам. Во втором пункте было сказано, что для любых двух предметов естественнонаучного цикла в методическом объединении должен быть ровно один представитель, являющийся специалистом по этим предметам. В третьем же — что в объединении должно быть ровно три специалиста по каждому предмету.

Когда Холмс рассказал ребятам об этом приказе, они удивились: ведь тут ничего нельзя понять; неизвестно, сколько учителей будет в объединении, и неизвестно, сколько различных специальностей они будут представлять.

Холмс ответил:

— Ничего подобного! Все ясно: в объединении будет шесть учителей, а различных специальностей будет четыре. Вы сейчас в этом сами убедитесь.

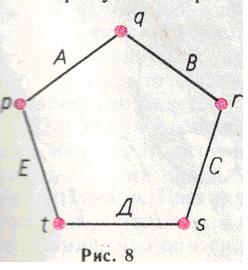
В первом условии сказано, что каждый член объединения должен быть специалистом по двум предметам. Если теперь заметить, что у каждого отрезка два конца, то совершенно ясно, что преподавателей можно изобразить отрезками, а их специальности — точками на концах этих отрезков (рис. 8).

Здесь каждый из преподавателей А, В, С, Д, Е имеет две специальности.

Преподаватель А, например, имеет две специальности р и q.

Обратимся теперь ко второму условию. Там сказано, что для любых двух предметов должен существовать ровно один преподаватель, являющийся специалистом по этим предметам. На нашем рисунке это условие не выполнено.

Для предметов р и q, например, нет преподавателя, являющегося специалистом по этим предметам. Чтобы второе условие было выполнено, надо провести в пятиугольнике р q г s t все диагонали. Получим рисунок 9.

Из этого рисунка видно, что каждой из специальностей p, q, r. s, t владеют по четыре человека (в каждой вершине сходятся четыре отрезка). В третьем же условии сказано, что по каждому предмету должно быть только три специалиста. Значит, пятиугольник не подходит (в нем слишком много диагоналей).

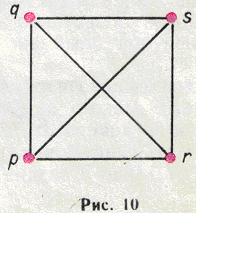
Попробуем теперь нарисовать четырехугольник (рис. 10): Нетрудно проверить, что сейчас все условия выполнены. Значит, в методическом объединении будет шесть преподавателей, которые будут представлять четыре предмета естественнонаучного цикла. По-видимому, этими предметами будут математика, физика, химия и биология.

Задача решена. Но хочется сделать еще одно интересное замечание. Для решения нашей задачи нам потребовалась схема, в которой были бы реализованы все условия задачи. Нарисовав такую схему, мы по существу построили модель той ситуации, которая описана в приказе директора. Число вершин и ребер этой модели не может быть изменено. Никакая другая фигура с другим количеством вершин и ребер не подходит. И в этом смысле можно сказать, что структура модели (число ее элементов, отношения и связи между ними) определена вполне однозначно.

Но форму модели можно изменить. Представим себе, например, что на рисунке 10

изображена пирамида с основанием р q r и вершиной s. Эта пирамида, очевидно, тоже будет моделью рассматриваемой ситуации. Но эта модель будет уже не плоской, а пространственной. Представим себе далее, что мы смотрим на эту пирамиду со стороны вершины s u при этом располагаем пирамиду таким образом, чтобы вершина s спроектировалась вовнутрь основания р q r. То, что мы увидим, изображено на рисунке 11:

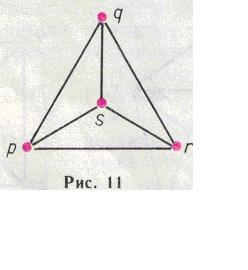
Мы ничего не изменили в нашей модели, мы только посмотрели на нее по-новому. Поэтому рисунок 11, очевидно, тоже может служить моделью рассматриваемой ситуации.

Мы можем видоизменить форму нашей модели еще одним способом.

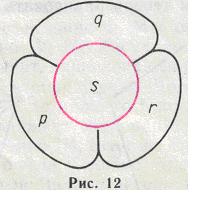
Представим себе, что точки p, q, r, s на рисунке 11 начинают «разбухать», превращаясь в кружочки. Продолжая разбухать, эти кружочки сначала придут в соприкосновение друг с другом, а потом, деформируясь, превратятся в фигуры, плотно прижатые друг к другу. Мы получим картину, изображенную на рисунке 12.

Это еще одна модель рассматриваемой ситуации. На этой модели специальностям p, q, r, s поставлены в соответствие плоские фигуры, а преподавателям — отрезки линий, по которым соприкасаются пары смежных фигур.

Надеюсь,что предложенные сюжеты паполнят Вашу методическую копилку и понравяться Вашим ученикам.