Семинар ДООМ Применение функций острого угла при решении практических задач

Автор: Дунаева Светлана Евгеньевна, IDm 137 Город Событий

Книга - книгой, а мозгами двигай.
Расстояния считай и на практике
Свои знания применяй!

Приложение
Презентация
Дополнительные задачи по теме

Цель урока:
Привитие интереса к предмету, активизация мыслительной деятельности, рассмотрение вопроса реализации учебных знаний с практической целью.

Подготовка к уроку:
на разных стенах классного кабинета развешены плакаты с высказываниями, определениями, историческими фактами из мира математики.

Примеры:

• Что, по преданию, завещал Архимед высечь на своем надгробном камне? (шар, вписанный в цилиндр)
• Назовите великого геометра и механика Дневней Греции, нашедшего значение числа пи.
• Циркуль – от лат. Circulus – «круг».
• Хорда от греч. «корде» - струна, тетина.
• Диаметр – от греч. «диаметрос» - поперечник, насквозь измеряющий
• Фигура, изобретенная в 1975г. преподавателем архитектуры из Будапешта (Кубик).

Оборудование:
компьютер, проектор.

Учитель:
Сегодня у нас состоится урок – конференция. Подумайте, какие знания и умения вы получаете за время учебы, умеете ли вы применять их при решении практических и нестандартных задач, помогает ли вам сообразительность и такой «инструмент» математики, как логическое мышление. Надеюсь, вы подготовились, прочитали дополнительную литературу, повторили основные формулы из курса геометрии. Звучит музыка.

Учитель:
Итак, мы начинаем.

1 этап.
Повторение.
Учитель предлагает повторить основные определения: прямоугольный треугольник, основные функции острого угла прямоугольного треугольника.

2 этап.
Выступление учащихся и совместное решение задач.

Выступление 1 – го ученика

Задача 1.
Пассажирский самолет, находящийся над пунктом А на высоте h=400 м, начал приземление на аэродром, расположенный в 2,5 км от пункта А. Как велик будет в среднем угол приземления самолета?

Решение:
Предположим, что точка приземления самолета В находится на одной горизонтальной плоскости с пунктом А. Из прямоугольного треугольника АВС находим тангенс искомого угла В: tg B = AC / AB = 400 м / 2500 м = 0,16. По таблице тангенсов находим, что угол В равен примерно 9 градусов. Ответ: 9 градусов.

Задача 2.
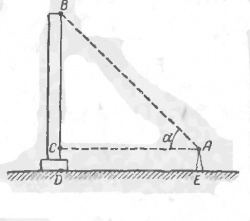
Допустим, что требуется определить высоту фабричной цилиндрической трубы, расположенной на горизонтальной площадке так, что к основанию трубы можно подойти.

Решение:

На некотором расстоянии АС=b м от основания трубы установим угломер и определим угол а между горизонталью и направлением на верхнюю точку В трубы. Применим к прямоугольному треугольнику АВС следствие установим, что
BC = AC tga
Учитывая высоту угломера АЕ = h м, получаем формулу для определения высоты трубы:
BD = h + b tga

По полученной формуле уч-ся самостоятельно просчитывают высоту, если входные данные были следующими: b= 40 м, h=1.5 м и угол а равен 30 градусам. Ответ: примерно 26 м.

Выступление 2–го ученика
Задача 3

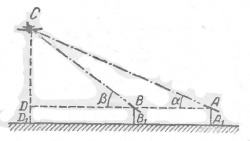
Как на практике определить на какой высоте летит самолет, если наблюдатели находятся в пунктах А и В (см рис).

Решение:
Два наблюдателя устанавливают в горизонтальной плоскости угломерные приборы АА1 и ВВ1 так, чтобы плоскость измерительных приборов АА1ВВ1 пересекла трассу полета самолета (см рис). Далее приборами фиксируются по сигналу углы а и b. Затем измеряют расстояние между угломерными приборами АВ = с метров и высоту приборов АА1=ВВ1= h метров.

Из прямоугольных треугольников CDB и CDA получаем:

CD =DB tgb (*)

CD =DА tga

откуда DB tgb = DА tga.

Но DА= DB+ВА = DB+с, отсюда

DB tgb= (DB+с)tga

DB = (с tga)/(tgb – tga)

Подставив значение DB в равенство (*), получим

CD = (с tga tgb )/(tgb – tga)

Таким образом, искомая высота полета самолета

CD1 = CD+ DD1 = (с tga tgb)/(tgb – tga) + h, так как DD1= ВВ1 = АА1 = h.

Ребята самостоятельно применяют выделенную формулу для конкретного случая проведенных наблюдений и соответствующих измерений. Пусть результаты измерения оказались следующими:
H = 1,5 м, с= 93,5м, угол а примерно 39 градусов, угол b примерно 44 градуса. Ответ: примерно 479 метров.

Выступление 3–го ученика
«Определение расстояния между двумя пунктами, к которым нельзя подойти»

Задача 4
С берега моря видны два предмета А и В, находящиеся на острове (см рис). Как определить расстояние между этими предметами, не совершая поездки на остров?