Семинар ДООМ Комбинаторика. Основные понятия.

Автор: Гурилева Любовь Владимировна, IDm153

Разработка: Гурилёвой Любови Владимировны, учителя математики

Цель и задачи:

Образовательные - ознакомить с определением комбинаторики, основными понятиями и формулами.

Развивающие – развить у учащихся интерес логическому мышлению, научить именять формулы комбинаторики для решения задач.

Воспитательные - воспитывать интерес к комбинаторным задачам, теории вероятностей, познакомить с историей возникновения комбинаторных задач.

Оборудование и материалы урока:
компьютерный класс, компьютерный проектор, экран, ИИП «КМ – школа». Тип урока: изучение нового материала. Продолжительность урока: 1 академический час. Методы обучения: просмотр презентации в ИИП «КМ – школа», обобщение материала - ответы на вопросы, задачи на дом.

Ход урока

1. Постановка цели урока Проверяется подготовленность классного помещения и готовность учащихся к уроку. Учитель: Сегодня будем рассматривать, что такое комбинаторика, её правила и применение полученных знаний к решению задач. Записывается тема урока: «Комбинаторика. Основные правила»

2. Подготовка к изучению нового материала Фронтально проверить домашнее задание. Ответить на вопросы учащихся. 3. Ознакомление с новым материалом ( с демонстрацией слайдов «КМ – школа»)

Правило 1.

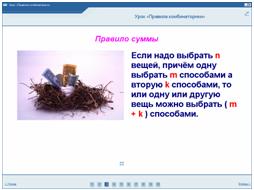
Задача: Имеется 8 шаров: в 1-й ящик положили 5 шт., а во 2-й – 3 шт. Сколькими способами можно вытащить 1 шар?

( ответ: 5 + 3 = 8 способами)

Правило 2.

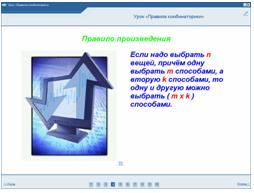
Задача: В 1 ящике 5 зеленых, а во 2-м 3 красных шара. Сколькими способами можно вытащить 1 зеленый и 1 красный шар?

( ответ: 5х3 = 15 способами)

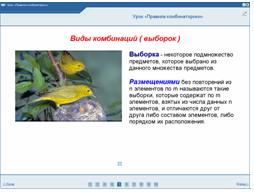
Учитель: в комбинаторике существуют виды комбинаций

Задача: В звене 12 человек. Требуется выбрать звеньевого, санитара, командира. Сколькими способами это можно сделать?

( ответ: звеньевого- 12 способами, санитара- 11 способами, а командира - уже 10. 12х11х10 = 1320 способов).

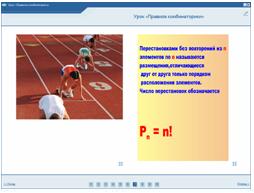
Правило 3.

Задача: Сколько четырехзначных чисел можно записать с помощью цифр 1,2,3,4, если каждая цифра входит в число только один раз?

( ответ: 4! = 1х2х3х4=24)

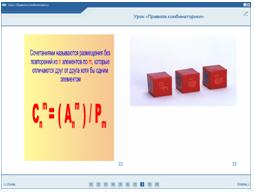
Правило 4.

Пример: На тренировке занимаются 10 баскетболистов. Сколько различных стартовых пятерок может образовать тренер? ( т. к. важно только количество, значит надо определить число сочетаний из 10 элементов по 5: = 252)

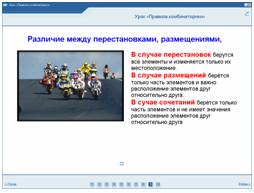
Учитель: Давайте сформулируем различия между размещениями, перестановками и сочетаниями.

4. Обобщение, закрепление материала. Учитель: А теперь каждый проверит себя и соседа.

5. Домашнее задание.

Задачи на дом: В спортивном лагере 8 команд, а на складе имеются синие, черные майки и трусы. Хватит ли на 8 команд комплектов спортивной формы? - в тренировках участвовали 12 баскетболистов. Сколько может образовать тренер различных стартовых пятерок? - сколькими способами можно зачеркнуть пять номеров из 36 в карточках лотереи «Спортлото»?

6. Резервные задания На случай досрочного выполнения всем классом рассмотренных заданий и обеспечения занятости и развития, наиболее подготовленных учащихся планируется использовать дополнительные задания.

На горку ведут 5 дорожек. Сколько имеется вариантов подъёма и спуска по этим дорожкам? В кружке юных математиков 25 членов. Сколькими способами можно выбрать председателя, заместителя, редактора стенгазеты и секретаря? В городе проводится первенство по футболу. Сколько в нём состоится матчей, если участвуют 12 команд?