Семинар ДООМ Использование компьютерных технологий при изучении темы: "Показательные уравнения"

Материал из ТолВИКИ

Версия от 18:54, 8 декабря 2010; Ивушкина Людмила Дмитриевна (обсуждение | вклад)

(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)

Участник:Ивушкина Людмила Дмитриевна, Участник:Одинцова А. М., Участник:Сканавики IDm198

Использование компьютерных технологий при изучении темы: "Показательные уравнения"

Цели урока:

Проверка знаний основных теоретических вопросов по теме “Показательная функция”.
Проверка знаний по темам “Использование условного оператора при составлении тестов”, “Стандартные функции TPascal”.
Введение понятия “показательное уравнение”.
Формирование навыков решения простейших показательных уравнений.
Умение анализировать и на основании экспериментальных данных делать выводы.
Воспитание познавательного интереса к математике и информатике.
Воспитание наблюдательности, самостоятельности, способности к коллективной работе.

Цель интеграции математики и информатики.
1. Совершенствование содержания образования.
2. Освоение и использование информационных технологий в учебном процессе.
Тип урока:
Компьютерная поддержка предмета (алгебра и начала анализа).
Форма работы:классно-урочная
Технология: Личностно-ориентированная; проблемно-исследовательская.
Время проведения: 9 неделя 1 четверти, 3 урок
Оборудование: Компьютерный класс, компьютерные программы “Графики 3.0.3”, “Turbo Pascal”, перфокарты, учебное домино, раздаточный материал, доска.
План урока
1. Организационный момент.
2. Постановка цели.
3. Проверка теоретического материала по математике и информатике.
3.1. Тестирование на ПК по теме “Показательная функция”.
3.2. Работа с учебным домино по информатике.
3.3. Устная работа.
4. Введение понятия показательного уравнения.
5. Работа с графикой на ПК.
6. Решение уравнений.
7. Программированный контроль.
8. Домашнее задание.
9. Подведение итогов.

Ход урока:
1. Организационный момент
2. Постановка цели.
Приветствие.
- Ребята, сегодня на уроке вам предстоит проверить знания основных теоретических вопросов по теме “Показательная функция”, используя при этом знания языка программирования Pascal. Так же, мы с вами введём новый для вас тип уравнений и научимся решать простейшие из них, при этом, при помощи компьютерной программы вы увидите графическое решение этих уравнений. Будьте собраны, внимательны и наблюдательны. Успехов!
3. Класс разбит на две группы.
Учитель информатики поясняет работу каждой из групп:
- Ребята, на предыдущих уроках мы учились писать тесты на языке программирования Pascal, используя условный оператор. Вы составляли тесты по информатике и математике. Я вам предлагаю тест по математике на тему “Показательные функции”. Прежде чем ответить на вопрос теста, вам придется перевести формулы, написанные на языке программирования Pascal, на математический язык. Первая группа садится за компьютер, нажимает на ярлык ТЕСТ и начинает тестирование. Вторая группа, должна составить цепочку домино. Тот, кто закончит работу с тестом или с домино может подумать над вопросом задачи, написанной на доске:
Найдите возможную закономерность последовательности:
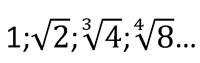
3.1. Первая группа садится за компьютеры и проходит тестирование по теме “Показательная функция” при помощи теста, составленного на языке программирования Pascal.
Тест “Показательная функция”
Критерии оценивания теста:
9-10 баллов – “5”
7-8 баллов – “4”
5-6 баллов – “3”
меньше 5 баллов – “2”
Тестирующая программа, написанная при помощи условного оператора на Pascal
Program TEST;
Var n,k:integer; {n – оценка, k – вариант ответа}
Begin writeln(‘1. Область определения показательной функции:’);
writeln(‘1). (0;+$)’);
writeln(‘2). R’);
writeln(‘3). [0;+$)’);
writeln(‘4). (-$;0)’);
readln(k);
if k=2 then writeln(‘Правильно’) else writeln(‘Неправильно’);
if k=2 then n:=n+1;
writeln;
writeln(‘2. Множество значений показательной функции’);
writeln(‘1). (-$;0)’);
writeln(‘2). R’);
writeln(‘3). (0;+$)’);
writeln(‘4). [0;+$)’);
readln(k);
if k=3 then writeln(‘Правильно’) else writeln(‘Неправильно’);
if k=3 then n:=n+1;
writeln;
writeln(‘3. Показательная функция y=exp(x*ln(a) возрастает на R при’);
writeln(‘1). a>1’);
writeln(‘2). a@R’);
writeln(‘3). 0<a<1’);
writeln(‘4). a>0’);
readln(k);
if k=1 then writeln(‘Правильно’) else writeln(‘Неправильно’);
if k=1 then n:=n+1;
writeln;
writeln(‘4. Показательная функция y=exp(x*ln(a) убывает на R при’);
writeln(‘1). a@R’);
writeln(‘2). a>1’);
writeln(‘3). 0<a<1’);
writeln(‘4). a<1’);
readln(k);
if k=3 then writeln(‘Правильно’) else writeln(‘Неправильно’);
if k=3 then n:=n+1;
writeln;
writeln(‘5. Упростить exp(5*x*ln(7))* exp(-5*x*ln(7))’);
writeln(‘1). exp(-25*x*ln(7))’);
writeln(‘2). 0’);
writeln(‘3). exp(x*ln(7))’);
writeln(‘4). 1’);
readln(k);
if k=4 then writeln(‘Правильно’) else writeln(‘Неправильно’);
if k=4 then n:=n+1;
writeln;
writeln(‘6. Функция y=exp(x*ln(0.2 )) убывает на множестве чисел’);
writeln(‘1). (0;1)’);
writeln(‘2). R’);
writeln(‘3). (1;+$)’);
writeln(‘4). (-$;1)’);
readln(k);
if k=2 then writeln(‘Правильно’) else writeln(‘Неправильно’);
if k=2 then n:=n+1;
writeln;
writeln(‘7. Функция y=exp(x*ln(2 )) проходит через точку‘);
writeln(‘1). (1;1)’);
writeln(‘2). (1;0)’);
writeln(‘3). (0;0)’);
writeln(‘4). (0;1)’);
readln(k);
if k=4 then writeln(‘Правильно’) else writeln(‘Неправильно’);
if k=4 then n:=n+1;
writeln;
writeln(‘8. Функция y=exp(abs(x)*ln(3 )) на множестве R‘);
writeln(‘1). Убывает’);
writeln(‘2). Возрастает’);
writeln(‘3). Немонотонна’);
writeln(‘4). Затрудняюсь ответить’);
readln(k);
if k=3 then writeln(‘Правильно’) else writeln(‘Неправильно’);
if k=3 then n:=n+1;
writeln;
writeln(‘9. Множество значений функции y=exp(x*ln(3 ))+1 ‘);
writeln(‘1). [-4;4]’);
writeln(‘2). (4;+$)’);
writeln(‘3). [1;+$)’);
writeln(‘4). (1;+$)’);
readln(k);
if k=4 then writeln(‘Правильно’) else writeln(‘Неправильно’);
if k=4 then n:=n+1;
writeln;
writeln(‘10. Область определения функции y=exp(sqrt(x+1)*ln(6/7 ))+1 ‘);
writeln(‘1). R’);
writeln(‘2). [-1;+$)’);
writeln(‘3). [0;+$)’);
writeln(‘4). [-1;1]’);
readln(k);
if k=2 then writeln(‘Правильно’) else writeln(‘Неправильно’);
if k=2 then n:=n+1;
writeln;
if n<5 then writeln(‘Оценка ‘,2);
if (n<=5) and (n<7) then writeln(‘Оценка ‘,3);
if (n>=7) and (n<=8) then writeln(‘Оценка ‘,4);
if n>8 then writeln(‘Оценка ‘,5);
readln;
End.
3.2. Вторая группа работает с учебным домино (состоит из 12 карточек).

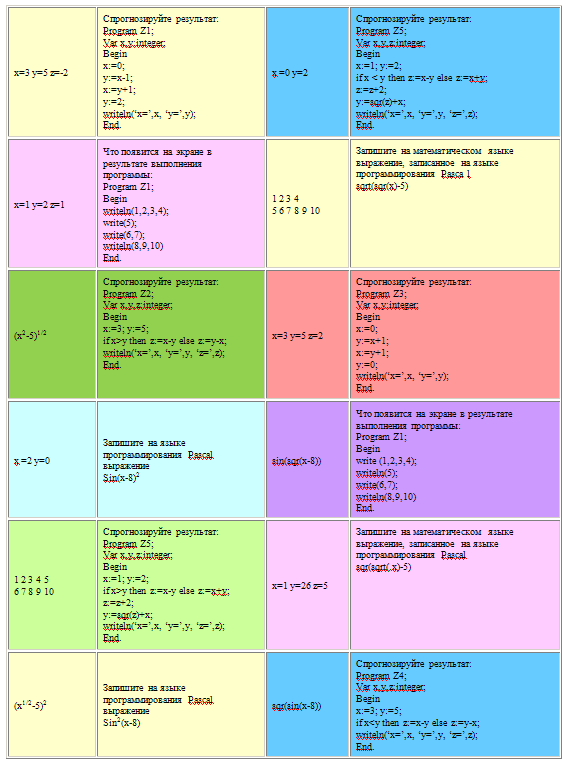
По окончании работы группы меняются видами деятельности: вторая группа идет тестироваться за компьютером, а первая - работать с домино. Затем все занимают рабочие места за партами.
3.3. Устная работа. Урок продолжает учитель математики.

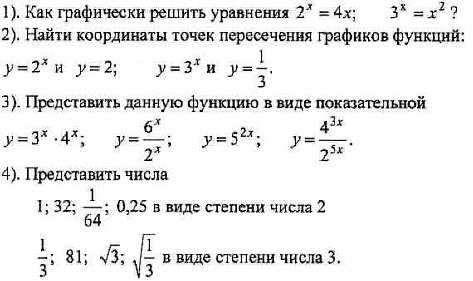
Введение понятия показательного уравнения.
Итак, для того, чтобы решить уравнение графически, надо найти абсциссы точек пересечения графиков функций обеих частей уравнения, а если одна или обе функции показательные, то это уравнение будет называться показательным.
Тема сегодняшнего урока “Показательные уравнения и решения простейших из них”.
В тетрадях запишите тему: Показательные уравнения и общий вид показательного уравнения:

Определение. Уравнение, содержащее переменную в показателе степени, называется показательным.
По раздаточному материалу показать, какими могут быть показательные уравнения и какие уравнения мы сегодня будем решать

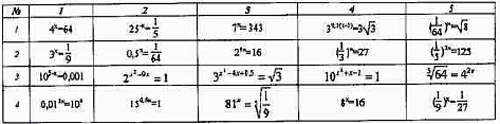
Работа с графикой на ПК. Урок продолжает учитель информатики.
- Ребята, используя программу “Графики 3.0.3”, решите графически уравнения.
С этой программой мы с вами уже работали, она позволит вам сэкономить время и сделать выводы о том, при каких значениях параметра b уравнение имеет решение, а при каких не имеет.
Учащиеся садятся за компьютеры (по 2 человека) и под руководством учителя информатики работают с программой “Графики 3.0.3”. Ученикам необходимо найти графическое решение предложенных уравнений и определить, при каких значениях b уравнения имеют решения [при b>0]. Какое свойство показательной функции отражается в этом выводе? [E(y)=R+].

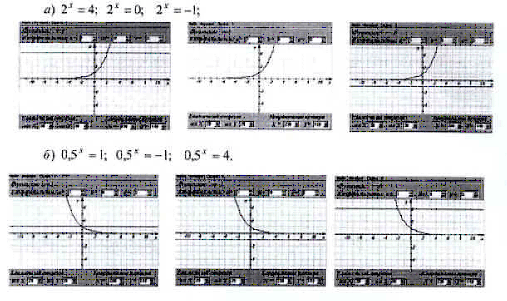
После работы с графической программой ребята занимают места за партой и продолжают работать с учителем математики.
Физкультминутка (за партами сидя).
Вывод из экспериментальных данных.
если уравнение имеет решение, то активно покивать головой вперед-назад и расправить плечи. если уравнение не имеет решения, помотать головой влево-вправо, после чего 2 раза закрыть глаза. Учитель математики: Уравнение можно решить, используя теорему о корне, напомните её.

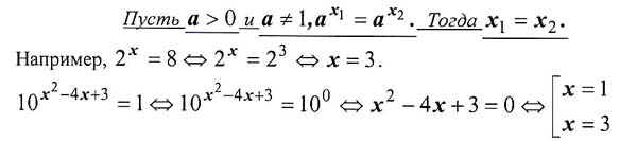
Обобщим все сказанное в виде блок-схемы: (учитель информатики).

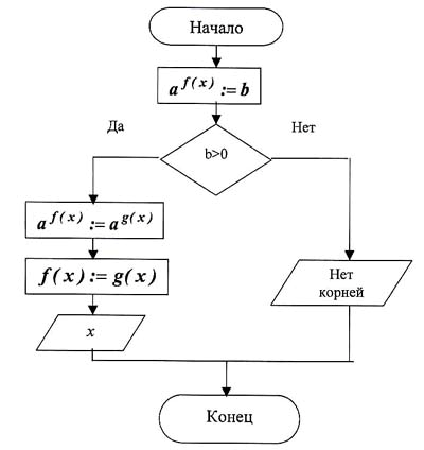
Урок продолжает учитель математики.
Как видно из блок-схемы, от показательного уравнения мы перешли к уравнениям, решать которые вы умеете (работа с раздаточным материалом, 1 столбик).
6. Решение уравнений (2 минуты самостоятельно, затем проверка у доски).
Решение уравнений №214-216 (нечетные).
7. Программированный контроль (по перфокартам, за 7 минут до конца урока).

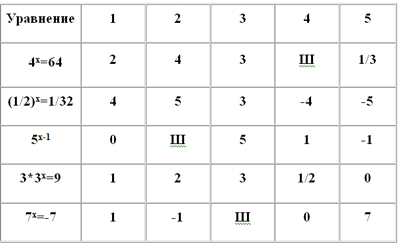
8. Домашнее задание:
Математика:
§12, №214-217 (четные)
Информатика: Написать программу и блок-схему для вычисления:

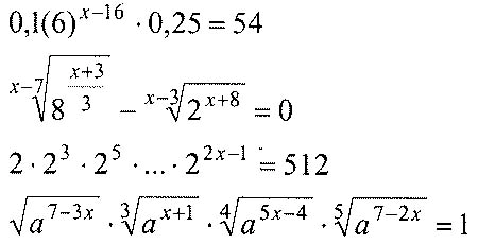
9. Подведение итогов. - О чём вы узнали на сегодняшнем уроке?
Сегодня мы рассмотрели только такие уравнения, обе части которых можно представить в виде степеней с одинаковым основанием, на следующих уроках будут рассмотрены более сложные уравнения и способы их решения.
Мы сегодня поработали с тестирующей программой в Pascal, проверили умение работать со стандартными функциями, операторами присваивания, ввода/вывода.
Работая с программой “Графики 3.0.3”, вы смогли сделать выводы к уроку.
Спасибо вам за урок!