Система счисления Штерна-Броко
Система счисления Штерна-Броко
Система счисления Штерна-Броко — способ записи положительных рациональных чисел, основанный на дереве Штерна-Броко.
Дерево Штерна — Броко — способ расположения всех неотрицательных несократимых дробей в вершинах упорядоченного бесконечного двоичного дерева.
В каждом узле дерева Штерна — Броко (иногда также называемого деревом Фарея) стоит медианта ![]() дробей
дробей ![]() и
и ![]() стоящих в ближайших к этому узлу левом и правом верхних узлах. Начальный кусок дерева Штерна — Броко в этом случае выглядит так:
стоящих в ближайших к этому узлу левом и правом верхних узлах. Начальный кусок дерева Штерна — Броко в этом случае выглядит так:
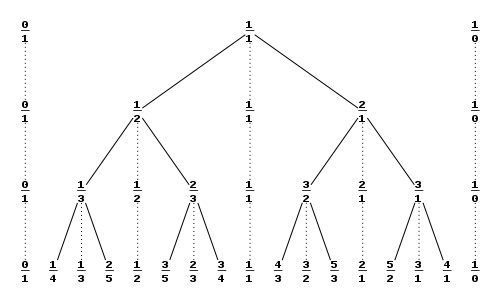
История
В книге Р. Грэхема, Д. Кнута, О. Паташника Конкретная математика открытие «дерева Штерна — Броко» связывается с именами Морица Штерна (1858) и Ахилла Броко (1860). Также была похожая система счисления была известна еще древнегреческим математикам и была построениа в форме «дерева Калкина-Уилфа".
Свойства
* Все дроби в деревьях Калкина — Уилфа и Штерна — Броко несократимы; * Каждая несократимая дробь появляется в дереве ровно один раз.
Для дерева Штерна — Броко доказательство основано на следующей лемме: если p1 / q1 < p2 / q2 — дроби в двух соседних узлах дерева, то q1p2 − q2p1 = 1.
Система счисления Штерна — Броко
Можно воспользоваться символами L и R для идентификации левой и правой ветви при продвижении вниз по дереву от корня, дроби 1/1, к некоторой определённой дроби. Тогда каждая положительная дробь получает единственное представление в виде строки состоящей из символов «R» и «L» (дроби 1/1 соответствует пустая строка). Такое представление положительных рациональных чисел назовём системой счисления Штерна — Броко. К примеру, обозначение LRRL соответствует дроби 5/7.
