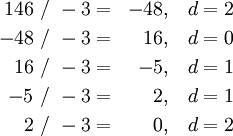Нега-позиционная система счисления

Cкомпоновал статью: Вадим Наумов

Н́ега-позици́онная сист́ема счисл́ения — это позиционная система счисления с отрицательным основанием. Особенностью таких систем является отсутствие знака перед отрицательными числами и, следовательно, отсутствие правил знаков. Всякое число любой из нега-позиционных систем, отличное от 0, с нечётным числом цифр — положительно, а с чётным числом цифр — отрицательно. Часто число в нега-позиционной системе требует для записи на одну цифру больше, чем то же число в системе с положительным основанием. Арифметика над нега-позиционными числами существенно проще из-за отсутствия записи «отрицательных» чисел, что хорошо отражается на машинной реализации и позволяет ускорить вычислительные процессы. Обычно название нега-позиционной системы состоит из префикса нега- и названия соответствующей системы счисления с положительным основанием; например, нега-десятичная (b = —10), нега-троичная (b = —3), нега-двоичная (b = —2) и другие.

История

Нега-позиционные системы счисления были впервые предложены Витторио Грюнвальдом в его работе «Giornale di Matematiche di Battaglini», опубликованной в 1885 году. Грюнвальд описал алгоритмы сложения, вычитания, умножения, деления, вычисления корня, проверки делимости и преобразования систем счисления.

Представление в разных системах

Представления чисел от -12 до 12 в различных системах счисления:

Десятичное	Нега-десятичное	Двоичное	Нега-двоичное	Троичное	Нега-троичное
-12	28	-1100	110100	-110	1210
-11	29	-1011	110101	-102	1211
-10	10	-1010	1010	-101	1212
-9	11	-1001	1011	-100	1200
-8	12	-1000	1000	-22	1201
-7	13	-111	1001	-21	1202
-6	14	-110	1110	-20	20
-5	15	-101	1111	-12	21
-4	16	-100	1100	-11	22
-3	17	-11	1101	-10	10
-2	18	-10	10	-2	11
-1	19	-1	11	-1	12
0	0	0	0	0	0
1	1	1	1	1	1
2	2	10	110	2	2
3	3	11	111	10	120
4	4	100	100	11	121
5	5	101	101	12	122
6	6	110	11010	20	110
7	7	111	11011	21	111
8	8	1000	11000	22	112
9	9	1001	11001	100	100
10	190	1010	11110	101	101
11	191	1011	11111	102	102
12	192	1100	11100	110	220

Перевод в нега-позиционные системы

Нега-позиционное представление числа может быть получено последовательными делениями с остатком исходного числа на b = − r (то есть на основание нега-позиционной системы) и записью подряд остатков начиная с последнего. Заметим, что если a / b = c, с остатком d, то bc + d = a. Пример перевода в нега-троичную систему:

$\begin{align} 146 & ~/~ -3 = & -48, & ~~~d = 2 \\ -48 & ~/~ -3 = & 16, & ~~~d = 0 \\ 16 & ~/~ -3 = & -5, & ~~~d = 1 \\ -5 & ~/~ -3 = & 2, & ~~~d = 1 \\ 2 & ~/~ -3 = & 0, & ~~~d = 2 \\ \end{align}$

Следовательно, нега-троичным представлением числа 146₍₁₀₎ является 21102_(-3).

Проверка знаний

тест по теме нега-позиционная система счисления

Используемые ресурсы

Википедия

Virtual laboratory wiki