Квадратные уравнения

Релейный урок

Учитель: Круглова Валентина Николаевна
Предмет: алгебра
Тема: квадратные уравнения
Тип урока: обобщающий
Продолжительность урока: 80 минут
Класс: 8
МОУ средняя школа № 90

Цели:

• Систематизировать и обобщить знания учащихся по изученной теме.
• Развивать умение наблюдать, сравнивать, обобщать, классифицировать, анализировать математические ситуации.
• Способствовать воспитанию таких качеств личности, как познавательная активность, самостоятельность, упорство в достижение цели.

Предварительная подготовка к уроку: подготовить экран.

Список класса (Ф.И.О. учащегося)

Подготовить карточки с заданиями трех уровней сложности:

• Простые карточки – синей цвет (Первый уровень).
• Карточки достаточного уровня – зеленый цвет (Второй уровень).
• Карточки повышенной сложности – красный цвет (Третий уровень).
• Нестандартные задачи – белый цвет

Педагогические технологии: разноуровневое обучение

Планируемый результат обучения:
Ученик на уроке должен показать умение решать квадратные уравнения с помощью:

• Общей формулы корней.
• Уметь решать уравнения a*x²+2k*x+c .
• Уметь находить корни квадратного уравнения по теореме Виета.
• Уметь раскладывать квадратный трехчлен на множители.

План урока

1. Математический диктант (проводится за компьютером).
2. Практическая работа.
3. Домашнее задание.
4. Итог урока.

1.Математический диктант

1) Выберите из приведенных уравнений: а) полное квадратное уравнение; б) неполное квадратное уравнение;

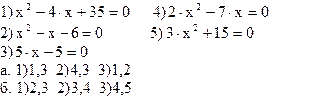
2) Как дискриминант влияет на количество корней квадратного уравнения? 1)D>0, 2 корня 1)D=0, 2 корня 1)D=0, 1 корень 2)D=0, 1 корень 2)D<0, 1корень 2)D>0, нет корней 3)D<0, нет корней 3)D>0, нет корней 3)D<0, 2 корня 3) Записать общую формулу для решения квадратного уравнения. 1) 2) 3) 4) По какой формуле удобнее решать уравнение вида 1) 2) 3) 5) Решить уравнения по теореме Виета: а) 1)5,6 2)3,8 3)4,6 б) 1)-2,1 2)-2,-1 3)3,1 в) 1)2,9 2)-2,-9 3)3,-6 6) Разложить на множители квадратный трехчлен  : 1) (x+5)(x-2) 2) (x-5)(x+2) 3) (x-3)(x-2)

7) Составьте квадратное уравнение корнями которого являются числа: и 1) 2) 3)

Ответы к диктант. 1) а)1,2; б)3,4; 2) 1; 3) 2; 4) 1; 5) а)2,3,8; б)2,-2,-1; в)2,9; 6) (x+5)(x-2); 7)  ;

2.Практическая работа

Мы с вами изучили тему квадратные уравнения. Рассмотрели различные способы решения уравнений. На столе разложены карточки трех уровней, по каждому из способов.

Каждый выбирает карточку своего уровня, если с ней справился, можно взять карточку уровня выше.

Учитель в таблице отмечает каждую карточку, и какой уровень выполнил ученик. В конце считает количество набранных баллов. Ученик сам перемещается по уровням и выполняет посильные ему задания.

А. I уровень

1) Решить уравнения:

II уровень

2) Решить уравнения:

III уровень

3) Решить уравнения:

Б. I уровень

1) Решить уравнения:

II уровень

2) Решить уравнения:

III уровень

3) Решить уравнения:

4) При каких значениях b уравнении имеет два различных корня

В. I уровень

1) Не используя формулу корней, найдите корни квадратного уравнения:

2) Составить квадратное уравнение, по известным корням:

3) Разложить на множители квадратный трехчлен:

II уровень

4) Сократить дробь:

5) Решить уравнение по теореме Виета:

6) Составить квадратное уравнение с заданными корнями

III уровень

7) При каких значениях k произведение корней квадратного уравнения

 равно нулю.

8) В уравнении , сумма квадратов корней равна 16.

  Найти значение а.

9) Не вычисляя корней уравнения , найдите

10) Разность корней уравнения , равно 2.5, найдите р и корни уравнения

11) Сократить дробь:

Решение готовлю в отдельной тетради. Критерии оценок сообщаются перед началом практической работы и он таковы:

             «3» надо набрать 18 баллов;
             «4» надо набрать 24 балла;
             «5» надо набрать 30 баллов;

Нестандартные задачи. 1) В уравнении , определить k так, чтобы один из корней был вдвое больше другого где > 0 , > 0 Ответ: нет решения. 2) Решить уравнение , и определить знаки его корня Ответ: при а>4,а<-1 3) Определить все значения а, при которых уравнение и имеют хотя бы один общий корень. Ответ: а = - 6. 4) При каких значениях, а уравнения имеет два различных корня? Определить знаки его корней в зависимости от а? За решение нестандартных задач, ученик получает дополнительную оценку.

3. Домашнее задание:

§20, §23, §24 I гр. №963(г), 966(г), 942, 819(б) II гр. № 998(б), 1001, 954, 849(б)

4. Итог урока

Подсчитать количество баллов, выставить оценки, согласно критериям, в журнал, на экран и в дневник. На уроке ученики получают по две оценки: за математический диктант и за практическую работу.