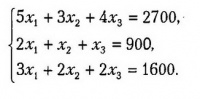Семинар ДООМ Компьютерное математическое моделирование в среде Excel на примере решения экономических задач (10 класс)

Автор: Дунаева Светлана Евгеньевна, IDm 137 Город Событий

ДУНАЕВА СВЕТЛАНА ЕВГЕНЬЕВНА, ГБОУ СОШ № 137 г. Санкт-Петербург

Приложение:

• Презентация к уроку
• Индивидуальная домашняя работа по карточкам

Тип урока:
интегрированный урок по математике, экономике, информатике.

Цель урока:
развитие навыков работы за компьютером, ознакомление с практическим применением таблиц при решении математических задач, рассмотрение связи математики и экономики.

Оборудование:
проектор, компьютеры.

1 этап. Объяснение учителя. Совместный разбор задач. Работа за компьютером над задачами 1 и 2.

2 этап. Самостоятельная работа за компьютерами.

3 этап. Подведение итогов урока.

4 этап. Домашнее задание.

Учитель:
В последние годы мы особенно отчетливо ощутили, что нет ничего важнее для общества, чем здоровая экономика. Научное исследование основ функционирования экономики – сложная и интересная деятельность. Математические методы в ней играют все возрастающую роль. Сегодня мы на уроке рассмотрим два типа задач, которые покажут нам, как при помощи математики и информатики решить ряд практических задач из области экономики.

1 этап.

Задача 1. «Построение кривых спроса и предложения»
Зависимость спроса на некоторый товар Y от его цены X выражается уравнением У=(2/х)+2, а зависимость предложения Z от цены товара – уравнением Z=х²+1. Найдите точку равновесия в диапазоне [0.2; 3] с шагом 0.2.

Решение:
Точка равновесия – это точка пересечения кривых спроса-предложения. Для построения этих кривых прежде всего необходимо ввести данные в рабочую таблицу.

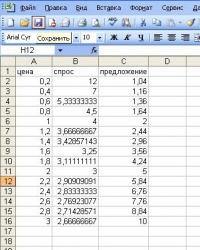
1. Вводим в ячейку А1 слово цена. В ячейку В1 слово спрос,в ячейку С1 – предложение.
   
2. Затем в ячейку А2 вводим первое значение аргумента - 0,2. Далее будем вводить приращение аргумента с шагом 0,2. Введем в ячейку А3 сумму левой границы диапазона плюс шаг, т.е 0,4. Затем, выделив блок ячеек А2:А3, автозаполнением получаем все значения аргумента.
3. Далее вводим значения функции спроса Y. В ячейку заносим формулу =2/А2+2 и нажимаем клавишу Enter. Скопируем формулу во все ячейки блока В3:В16. Таким образом значения спроса получены.
4. Аналогично получаем значения предложения Z. В ячейку С2 вводим формулу =А2*А2+1. Скопируем ее в диапазон С3:С16.
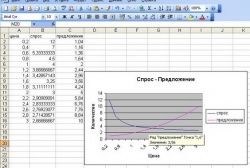
5. Далее по введенным в рабочую таблицу данным строим диаграмму. На панели инструментов вызываем Вставка / Диаграмма. Выбираем тип диаграммы График, вид – левый верхний. После нажатия кнопки Далее с помощью мыши указываем диапазон данных В1:С16. Проверяем положение переключателя Ряды в:столбцах. Выбираем вкладку Ряд и с помощью мыши вводим диапазон подписей по оси х – А1:А16. Нажав кнопку Далее, вводим название диаграммы – Спрос-Предложение, название осей х и у – Цена и Количество, соответственно. Нажимаем кнопку Готово.
6. Как видно из диаграммы, система имеет точку равновесия (точку пересечения кривых). Для ее нахождения необходимо навести указатель мыши на точку пересечения кривых и щелкнуть левой кнопкой. Появляется надпись с указанием искомых координат (точка 1.6 и ее значение 3.56). Здесь точке х соответствует цена, точке у – количество товара.
   

Задача 2.
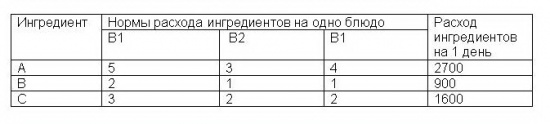
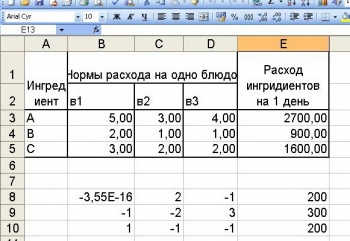
Ресторан специализируется на выпуске трех видов фирменных блюд: В1, В2, В3, при этом используются ингредиенты трех видов А, В, С. Нормы расхода каждого их них на одно блюдо и объем расхода ингредиентов за 1 день заданы таблицей. Найти ежедневный объем выпуска фирменных блюд каждого вида.

Решение:
Пусть ресторан ежедневно выпускает х1 блюд вида В1, х2 – вида В2, х3 – вида В3. Тогда в соответствие с таблицей расхода ингредиентов каждого вида имеем систему.

Задача сводится к решению данной системы. Выполним эту задачу с помощью таблицы Excel.

1. Заполним таблицу по образцу. Вводим коэффициенты уравнений системы в диапазон В3:D5.
2. Выполним действия:
   • выделим блок ячеек блок В8:D10;
   • нажмем на панели инструментов Стандартная кнопку Вставка функции;
   • в появившемся диалоговом окне Мастер функций в рабочем поле Категория выберите пункт Математические, а в рабочем поле Функция – имя функции – МОБР.
   • щелкните кнопку ОК;
   • отодвиньте в сторону появившиеся диалоговое окно МОБР мышью и введите диапазон исходной матрицы В3:D5 в рабочее поле Массив (указатель мыши при нажатой левой кнопке). Нажмите сочетание клавиш CTRL+SHIFT+ENTER. В результате в диапазоне В8:D10 появится матрица коэффициентов системы;
3. Находим решение данной системы:
   • выделим блок ячеек Е8:Е10;
   • нажмите на панели инструментов Стандартная кнопку Вставка функции;
   • в появившемся диалоговом окне Мастер функций в рабочем поле Категория выберите пункт Математические, а в рабочем поле Функция – имя функции – МУМНОЖ.
   • щелкните кнопку ОК.
   • отодвиньте в сторону появившиеся диалоговое окно МУМНОЖ мышью и введите диапазон В3:D5 в рабочее поле Массив 1 (указатель мыши при нажатой левой кнопке), а диапазон D1:D3 в рабочее поле Массив 2. Нажмите сочетание клавиш CTRL+SHIFT+ENTER.В результате в диапазоне D4:D6 появиться решения нашей системы: х1=200, х2=300, х3=200.

2 этап.

Задачи для самостоятельного решения.

1. Зависимость спроса на некоторый товар Y от его цены X выражается уравнением У=lnx, а зависимость предложения Z от цены товара – уравнением Z= - 2x+1. Найдите точку равновесия в диапазоне [0.2; 3] с шагом 0.2.
2. В трех торговых точках проведена ревизия и получены следующие данные о количестве проданных товаров трех видов. В кассе 1-го магазина обнаружено 31.8 условной денежной единицы, 2-го- 154,6 , 3-го – 141, 1. Требуется определить. По какой цене продавался каждый вид товара.

3 этап. Подведение итогов урока.

4 этап. Индивидуальная домашняя работа по вариантам.

Список используемой и рекомендованной литературы.

• Могилев А.В. Информатика: Учеб. пособие для студентов пед. вузов. М.: Москва, Из-во "Академия", 2000 г.
• Белошапка В.К. Информационное моделирование в примерах и задачах. Омск, ОГПИ,1992 г.
• Мур, Джеффри, Лари Р и др.Экономическое моделирование В Ecxel. 6-е издание. Пер. с анг. М.: «Вильямс», 2004 г.
• Математика в экономике. Учебно-методическое пособие. Под ред. Н.Ш.Крамера. М.: Финстатинформ, 1999 г.