Семинар ДООМ: Задачи на построение циркулем и линейкой. 7 класс

Автор: Шувалова Юлия Григорьевна

Тема урока: Задачи на построение циркулем и линейкой

Класс: 7

Тип урока: урок проверки и коррекции знаний и умений

Методы и приёмы ведения урока:

• фронтальная работа с классом;
• закрепление: работа учащихся в группах.

Цели урока:

Обучающая: проверка знания учащимися фактического материала по теме «Задачи на построение циркулем и линейкой»; умений учащихся самостоятельно применять знания в измененных нестандартных условиях.

Развивающая: развивать способность учащихся переносить ранее изученные знания и умения в новую ситуацию.

Воспитательная: воспитывать ответственное отношение к учебе, воли и настойчивости для достижения конечных результатов.

Оборудование:

• раздаточный материал (карточки с задачами).
• цветные карточки: по две на каждого ученика.
• ватман с названиями «В начале урока», «В конце урока» с конвертами.

Задачи урока:

1. обобщить знания учащихся по теме «Задачи на построение циркулем и линейкой»
2. повторить простейшие построения, которые являются стандартными построениями циркулем и линейкой; основные этапы, из которых состоит осмысленное решение задач на построение и смысл каждого этапа; основной метод решения задач на построение.
3. проверить знания учащихся по теме «Задачи на построение циркулем и линейкой».

Ход урока

I. Организационный момент

II. Постановка цели и задач урока.

Ребята должны

знать: стандартные построения циркулем и линейкой, основные этапы решения задач на построение и их смысл.

уметь: применять знания и умения по теме «Построение циркулем и линейкой» при решении задач.

III. Вводная часть

Учитель предлагает отметить свое настроение в начале урока. Для этого ребятам предлагается положить одну карточку в соответствующий конверт под строкой «В начале урока».

IV. Актуализация опорных знаний

Учитель предлагает учащимся устно ответить на предложенные вопросы, которые заранее записаны на интерактивной доске.

1. Какие простейшие построения являются стандартными построениями циркулем и линейкой?

Ответ: построить отрезок, равный данному отрезку; построить середину отрезка; построить перпендикуляр к прямой; построить серединный перпендикуляр; построить угол, равный данному углу; построить биссектрису угла.

2. Какие построения мы добавляем к стандартным построениям циркулем и линейкой?

Ответ: построить треугольник (по трём сторонам, по двум сторонам и углу между ними, по стороне и двум прилежащим к ней углам); построить прямоугольный треугольник (по гипотенузе и катету, по гипотенузе и острому углу); построить прямую, проходящую через данную точку параллельно данной прямой; построение отрезков суммы и разности отрезков, отрезка в n раз больше данного; построение углов суммы и разности двух углов; построение угла в n раз больше данного угла; деление данного угла на 4; 8; 16;… равных углов.

3. Из каких основных этапов состоит осмысленное решение задач на построение?

Ответ: осмысленное решение задач на построение состоит из 4 основных этапов: анализ, построение, доказательство (синтез), исследование.

4. В чем смысл каждого этапа решения задач на построение?

Ответ:

Анализ. Составляется план решения. Нужно найти такую зависимость между данными и искомыми величинами, которая позволила бы определить положение искомой точки (отрезка или угла), на нахождение которых нацелено решение задачи.

Построение – механическое выполнение тех приемов, которые были выведены из плана решения задачи, т.е. анализа. Любая задача на построение разбивается на конечное число шагов (простейших задач на построение).

Доказательство. Когда искомая фигура построена, необходимо доказать, что она удовлетворяет всем требованиям задачи. При этом ход рассуждений будет обратный тому, который применялся при анализе.

Исследование имеет целью выяснить, всегда ли задача разрешима, сколько решений допускается (одно или несколько). Необходимо рассмотреть всевозможные частные случаи, причем нужно выяснить, меняется ли ход решения в них и как именно.

5. Как называется и в чем заключается метод решения задач на построение?

Ответ: Для выполнения основных построений с помощью циркуля и линейки используется метод решения, при котором искомую точку строят как точку пересечения множеств (геометрических мест), определяемых некоторыми условиями.

V. Повторение и закрепление изученного материала

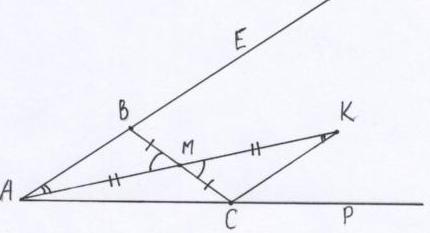
Задача 1: Дан угол и точка внутри него. Постройте отрезок с концами на сторонах угла и серединой в этой точке.

Анализ: Дан угол ЕАР и точка М внутри угла. Пусть ВС искомый отрезок, удовлетворяющий условиям задачи: ВМ=МС, В на АЕ, С на АР. Проведем АМ, откладываем на его продолжении отрезок МК=АМ. Треугольники АМВ = КМС (по I признаку). У них: углы ВМА= КМС (вертикальные), АМ=МК, ВМ=МС. Следовательно, углы ВАМ= МКС. Значит, построение ВС сводится к построению точки С на АР, т.е. к построению АК=2АМ и углов МКС= ВАМ.

Построение:

1) Проводим луч АМ, откладываем на его продолжении МК=АМ.

2) Строим углы МКС = ЕАК. Получаем С на стороне АР угла ЕАР.

3) Проводим луч СМ, получаем В на луче АЕ.

Отрезок ВС – искомый.

Доказательство: При построении получаем треугольники АМВ = КМС (по II признаку). У них: углы ВМА= КМС (вертикальные), АМ=МК (по построению), углы ВАМ= МКС (по построению). Следовательно, ВМ=МС. Получаем ВС – искомый отрезок.

Исследование: Построение выполнимо всегда, т.к. сводится к построению отрезка, равного данному, и угла, равного данному.

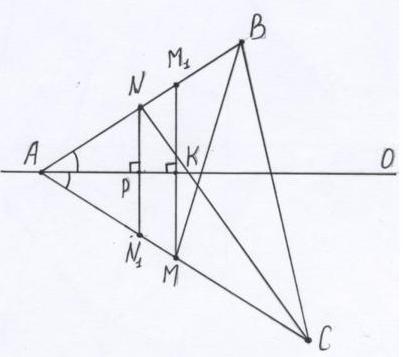
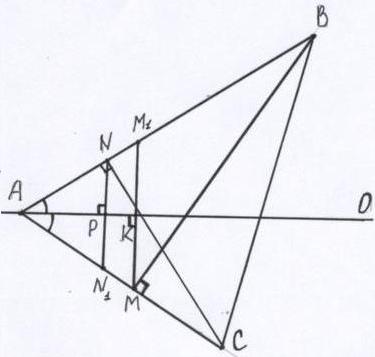
Задача 2. Дана прямая, на которой лежит биссектриса угла A треугольника ABC. По разные стороны от этой прямой даны две точки – основания: а) медиан; б) высот, проведенных из вершин B и C. Восстановите треугольник ABC.

Анализ: Пусть треугольник АВС (луч АО – биссектриса А, медианы СN, ВМ) – искомый. Проведем ММ1||АО и NN1||АО. Треугольники АКМ= АКМ1 (треугольники АРN= АРN1) (по II признаку). У них: 1) АК (АР) – общая, 2) углы АКМ= АКМ1=90 градусов (углы АРN= АРN1=90 градусов), 3) углы КАМ= КАМ1 – АО биссектриса А. Получаем, что точки М, М1 лежат на АС, а N, N1 лежат на АВ и находятся на одном расстоянии от АО. Аналогично, если точки N, М – основания высот.

Построение:

а)

1) Строим МК перперндикулярно АО и NР перпендикулярно АО. Откладываем КМ1=КМ и РN1=РN. Проводим прямые МN1 и NМ1, получаем А на пересечении АО, МN1 и NМ1.

2) Откладываем МС=АМ и NВ=АN. Проводим ВС.

Треугольник АВС построен.

б)

1) Строим МК перперндикулярно АО и NР перперндикулярно АО. Откладываем КМ1=КМ и РN1=РN. Проводим прямые МN1 и NМ1, получаем А на пересечении АО, МN1 и NМ1.

2) Строим МВ перперндикулярно АМ (В – точка пересечения МВ и АВ), NС перперндикулярно NА (С – точка пересечения NВ и АМ).

Треугольник АВС построен.

Доказательство: В обоих случаях мы получаем: точки М и М1 лежат на АС, N и N1 лежат на АВ. Треугольники АКМ= АКМ1 (по I признаку). У них: 1) АК – общая, 2) углы АКМ= АКМ1=90 градусов, 3) КМ= КМ1 – по построению. Углы КАМ= КАМ1, т.к. АО биссектриса А. а) точки N, М – основания медиан, т.к. по построению МС=АМ и NВ=АN. б) точки N, М – основания высот, т.к. по построению МВ перпендикулярно АМ, NС перпендикулярно NА.

Исследование: задача не имеет решения, если точки N, М находятся на одном расстоянии от АО. При этом МN1||AO, NМ1||AO МN1||NМ1 точку А построить невозможно.

Задача 3: Построить прямоугольный треугольник по гипотенузе с и сумме катетов .

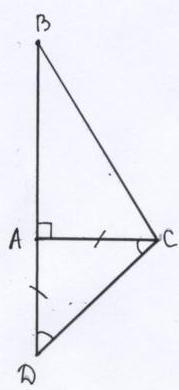
Анализ: Пусть треугольник АВС (угол А=90 градусов) построен. На луче ВА отложим отрезок AD = AC. Получим треугольник АDС – равнобедренный, в котором углы С и D равны половине угла А, т.е. 45 градусов (свойство внешнего угла треугольника). Задача сводится к построению треугольника ВСD по двум сторонам BD = b+а, ВС = с и угол D=45 градусов. Чтобы получить точку А, достаточно провести СА перпендикулярно DВ.

Построение:

1) Строим треугольник ВСD: BD = b+а, ВС = с и угол D=45 градусов.

2) Проводим СА перпендикулирно DВ.

Треугольник АВС – искомый.

Доказательство: При построении получаем треугольника АDС (угол А=90 градусов – по построению)угол CDA=45 градусов следовательно угол АСD= 45 градусов следовательно АС=DC. Т.к. ВС = с , BD = b+а, то АВ+АС= BD = b+а. Значит, треугольник АВС – искомый.

Исследование: Построение выполнимо если b+а>с.

Задача 4. Постройте треугольник по данной стороне, углу, к ней прилежащему, суммы двух других сторон.

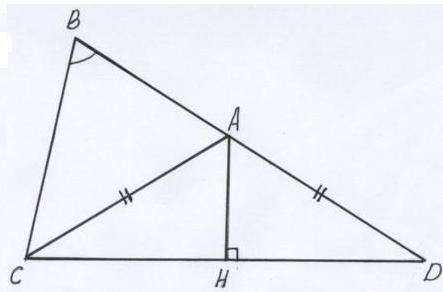
Анализ: Пусть треугольник АВС – искомый. На продолжении АВ отложим AD=CA. Соединим C и D. В треугольнике CBD имеем: BD = b+c, BC = a, угол СBD = углу B. Треугольник CBD можно построить по двум сторонам и углу между ними. Треугольник CAD – равнобедренный: АН – высота, медиана. Проведя серединный перпендикуляр АН к CD, определяем вершину А.

Построение:

1) Строим треугольник CBD: BD = b+c, BC = a, угол СBD = углу B.

2) Проводим серединный перпендикуляр АН к CD и получаем вершину А.

Треугольник АВС – искомый.

Доказательство: При построении получаем треугольник CBD: BD = b+c, BC = a, угол СBD = углу B. Также треугольник CАD: СН=HD, АН перпендикулярно CD следовательно треугольники АНС = АHD (по катетам)следовательно АС=AD. Т.к. BD = b+c, то ВА+АС= BD = b+c. Треугольник АВС – искомый.

Исследование: Построение выполнимо если b+а>с.

Задача 5. Постройте треугольник по двум углам и периметру.

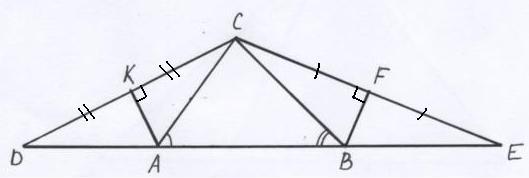
Анализ: Пусть треугольник АВС – искомый. На продолжении стороны АВ в обоих направлениях отложим отрезки DA = АС и ВЕ = СВ и соединим D с С и Е с С, получим треугольник DCE, в котором DE = Р. Треугольники DAC и ВЕС – равнобедренные, и АК перпендикулярно DC, где DK = KC и BF перпендикулярно FE, что позволит определить вершины А и В. Угол D= половине угла А, угол Е= половине угла В (свойство внешнего угла треугольника). Задача сводится к построению треугольника DCE по стороне DE=Р и углам D и E.

Построение:

1) Строим угол D = половине угла А, угол Е = половине угла В (биссектрисы углов).

2) Строим треугольник DCE: DE=Р, угол D, угол E.

3) Проводим серединные перпендикуляры АК к DC и BF к FE, получаем вершины А и В.

Треугольник АВС – искомый.

Доказательство:

1) При построении получаем:

1. Треугольник CАD: СК=КD, АК перпендикулярно CD следовательно треугольники АКС = АКD (по катетам) следовательно AD=CA

2. Треугольник CВЕ: СЕ=FE, BF перпендикулярно CE следовательно треугольники CFB = BFE (по катетам) следовательно CF=FE

2) DE = DA+AB+BE = CA+AB+BC = P

3) Угол BAC= удвоенному углу D, угол CBA = удвоенному углу E (свойство внешнего угла треугольника) следовательно углы В и А – искомые.

Значит, треугольник АВС – искомый.

Исследование: Построение выполнимо если угол В + угол А < 180 градусов.

IV. Физкультминутка (в середине урока)

Учитель проводит с учащимися упражнения для расслабления глаз.

VI. Домашняя работа

Дома: № 356, №354

VII. Итог урока

Учитель подводит итог урока:

• Что нового узнали на уроке?
• Какая задача удивила?

Учитель предлагает отметить свое настроение в конце урока. Для этого ребятам предлагается положить вторую карточку в соответствующий конверт под строкой «В конце урока».

Учитель объявляет оценки за урок.

Список используемой литературы

1. Атанасян Л.С. Геометрия 7-9. М.: Просвещение, 2005. - 335 с.
2. Далингер В.А. Планиметрические задачи на построение. Омск: Изд-во ОГПИ, 1999. - 78 с.
3. Ильина Н.И. Геометрические построения на плоскости. М.: Школа - пресс, 1997. - 172 с.
4. Коренева В.Е. Решение задач на построение методом спрямления. Математика в школе.1995г. №5
5. Клименченко С.В., Цикунова Т.Д. Задачи на построение треугольников по некоторым данным точкам. Математика в школе. 1990г. №1
6. Белошистая А.В. Задачи на построение в школьном курсе геометрии. Математика в школе. 2002г. №9
7. [1]
8. [2]