|
МОУ СОШ № 16, г. Жигулевск Сайт школы
Тема урока: "Проценты на Едином Государственном экзамене"
Тип урока: урок применения знаний и совершенствования умений и навыков
Вид урока: урок – игра «Исправляем ошибки»
Образовательная технология: развитие критического мышления
Цели:
1. проверить знание и понимание теоретического материала по теме «Проценты»;
2. совершенствовать умения строить логическую цепочку рассуждений, проводить обобщение и совершенствовать навыки применения знаний в новой ситуации;
3. стимулировать учащихся применять информационных технологии на уроках математики в плане поиска и изучения материала, решения заданий.
1. развитие критического мышления, внимания, умения обосновывать свою точку зрения;
2. создать условия для проявления познавательной активности учащихся, способствовать развитию математического кругозора.
1. содействовать воспитанию интереса к математике, воспитывать чувство целеустремлённости, самостоятельности и самоконтроля;
2. формировать способность к коллективной работе для достижения совместных целей.
Задачи:
1. научить применять теорию для решения задач повышенного уровня;
2. развивать творческую сторону мышления;
3. формировать навыки умственного труда - поиск рациональных путей решения.
Оборудование:
Карточки с правилами игры и со схемой составления эссе, компьютер, мультимедийный проектор, экран, текст заданий с неверным решением.
План урока:
1. Организационный момент;
2. Сообщение темы, цели и задач урока; знакомство с условиями игры;
3. Постановка учебной проблемы «Верно ли выполнено задание?», поиск типичных ошибок при анализе предложенных решений;
4. Самостоятельное выполнение заданий в группе, внешний контроль и самоконтроль;
5. Подведение итогов. Письменная рефлексия - написание эссе. Творческое домашнее задание - выпуск газеты, составление задач на проценты.
Методы обучения на уроке:
• Частично-поисковый;
• Проблемно-сообщающий.
Формы обучения:
Диалог;
Групповая;
Индивидуальная.
Ход урока.
1. Организационный момент;
Добрый день. Эффект урока будет зависеть от нашего взаимопонимания и слаженной работы. На каникулы вам было задано задание - повторить теоретический материал, связанный с процентами, который выложен на школьном сайте. Кроме теории там разобраны способы решения задач, оформление их условий, чтобы избежать ошибки. Теперь настало время продемонстрировать свои знания.
Девиз нашего урока: В математике следует помнить не формулы, а процессы мышления.
2. Сообщение темы, цели и задач урока.
Сегодня, используя эти знания, мы посвятим наш урок решению задач повышенного уровня, которые включены так же в материалы ГИА и ЕГЭ, цели и задачи урока записаны на доске. Урок будет проходить в виде игры «Исправляем ошибки».
3. Знакомство с условиями игры.
Для проведения игры разделимся на группы по 5 человек. Каждая группа получает одну и ту же задачу на проценты с предложенным решением, в котором имеются типичные ошибки ребят, сдававших экзамен в форме ЕГЭ. Вы должны указать эти ошибки, осмыслить содержание задачи, выстроить план практических действий и выполнить правильно задание. Та группа, которая первой успеет подготовиться, дает свою версию. Если её ответ будет неверным, с точки зрения жюри (учитель, три лучших ученика класса), то другие группы имеют возможность доказать свою точку зрения. За верный ответ группа получает пять баллов и правильное решение выносится на доску. Если у другой группы имеется другой способ решения, то он заслушивается и сравнивается с первым по рациональности решения. После выступления у доски все группы получают следующую задачу. Вы должны за урок исправить решение пяти задач. Это наша учебная проблема на сегодня. Желаю удачи всем присутствующим.
4. Самостоятельное решение задач.
Задача №1. В школе девочек на 25% больше, чем мальчиков. На сколько % мальчиков меньше, чем девочек.
Решение (с ошибкой):
1) Пусть х% составляют мальчики, тогда девочек (х+25)%, всего (х+х+25)%, что составляет 100%. Получаем уравнение х+х+25=100; х=37,5%
2) 62,5%-37,5%=25%
Ответ: на 25%.
После анализа решения озвучивается версия ошибки: количество мальчиков надо принимать за х, а не количество % и надо рассматривать отношение разности к количеству девочек, а не к количеству учеников.
Верное решение:
Пусть х мальчиков в школе, тогда девочек 1,25 х, и на (1,25-х) человек меньше, чем девочек мальчиков, что составляет 0,25x*100%/1,25x = 20%.
Ответ: на 20%.
Задача №2. Летом Женя похудел на 10%, а к Новому Году поправился на 10%. Поправился ли Женя, и если вес его изменился, то на сколько %.
Решение (с ошибкой):
Пусть 100% составил вес Жени, тогда после лета вес Жени составлял 90%,а к Новому году вес Жени опять составил 90%+10% = 100%.
Ответ: Женя не поправился.
После анализа решения озвучивается версия ошибки: вес Жени после Нового года увеличился на 10% от 90%, т.е. увеличился на 9%
Верное решение:
Пусть х кг – вес Жени, тогда после лета вес Жени стал 0,9х, а после Нового года его вес стал (0,9х+0,1*0,9х) кг, т.е. 0,99х, что составляет 0,99x*100%/x= 99%. Вес Жени уменьшился на 1%.
Ответ: Женя похудел на 1%.
Задача №3. Костюм состоит из пиджака, брюк и жилета. Пиджак дороже брюк на 26% и дороже жилета на 60%. На сколько процентов жилет дешевле брюк.
Решение (с ошибкой):
Пусть х% стоит пиджак, тогда брюки стоят (х-26)%, а жилет (х-60)%. Находим разность между ценой жилета и брюк: (х-26)-(х-60) = 34%.
Ответ: на 34% жилет дешевле брюк.
После анализа решения озвучивается версия ошибки: цена пиджака дана относительно двух величин, связь между которыми надо найти, а затем найти отношение разности цен относительно брюк.
Верное решение:
Пусть х рублей стоят брюки, тогда пиджак стоит 1,26х рублей. Пусть у рублей стоит жилет, тогда пиджак стоит 1,6у рублей. Т.к. стоимость одна и та же, то 1,26х = 1,6у или 126х = 160у.
Выразим у. у = 63x/80. Разность между ценой жилета и брюк: х-63x/80 = 17x/80 , что составляет от стоимости брюк (17x*100%/80)/x= 21,25%.
Ответ: на 21,25% жилет дешевле брюк.
Задача №4. Стоимость футболки после двух повышений на одно и то же число процентов изменилась с 500 рублей до 720 рублей. На сколько процентов повышалась цена футболки каждый раз?
Решение (с ошибкой):
1) Найдем разность рублей в стоимости футболки 750-500 = 220 рублей.
2) Выразим эту разность в процентах 220*100%/500 = 44%.
3) Т.к. повышение шло 2 раза на одно и то же число процентов, то 44:2 = 22%.
Ответ: на 22% повышалась цена футболки каждый раз.
После анализа решения озвучивается версия ошибки: второе повышение цены футболки рассчитывается не от первоначальной цены, а от новой.
Верное решение:
Пусть на х % повышалась цена футболки каждый раз, тогда после первого повышения цена стала 50*(1+x/100) рублей, а после второго повышения цена стала 500*(1+x/100)* (1+x/100)рублей, что составляет 720 рублей. Составим уравнение:
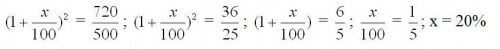
Ответ: на 20% повышалась цена футболки каждый раз.
Задача №5. При повышении цены билета на 29% число зрителей уменьшилось на 23%. На сколько процентов уменьшилась выручка театра?
Решение (с ошибкой):
Пусть цена билета была х рублей, тогда после повышения она стала 0,29х. Пусть у человек было зрителей, а стало 0,23у человек. Тогда ху – была выручка, а стала 0,29х*0,23у = 0,0667ху. Выручка уменьшилась на ху – 0,0667ху = 0,9333ху, что составляет 93,33%.
Ответ: на 93,3% уменьшилась выручка театра.
После анализа решения озвучивается версия ошибки: при повышении величины х на 29 %, она становится 1,29х.
Верное решение:
Пусть х рублей – цена билета, а у человек – количество зрителей, тогда ху рублей – выручка театра. После изменения 1,29х – цена билета, а 0,77у – количество зрителей, и выручка станет 0,77у*1,29х = 0,9933ху. Выручка уменьшилась на ху-0,9933ху = 0,0067ху, т.е. 0,67%.
Ответ: на 0,67% уменьшилась выручка театра.
5. Подведение итогов.
Итак, мы разобрали с вами пять задач с типичными ошибками. Убедились, что никто из нас от ошибок не застрахован, но при совместном поиске, когда идёт письменная запись решения, которая затем проговаривается и анализируется, ошибки становятся «видимыми» и «исправимыми». И каждый из вас приобретает личный опыт в умениях и навыках решать задачи на проценты и делает для себя выводы по проблеме «Верно ли решение?». Мне, как учителю интересно, какие выводы вы вынесли, чем вам интересен такой урок, что вы приобрели нового. Я попрошу вас проанализировать вашу собственную деятельность на уроке и написать эссе. Модель написания эссе у вас имеется на столе, пишется в произвольной форме каждой группой за 10 минут. По окончании данного времени зачитаем каждое эссе и получаем домашнее задание:
1) создать алгоритм правильного решения собственной задачи на проценты, т.е. сформулировать вопросы, на которые надо ответить ученику, чтобы найти правильное решение;
2) выбрать редколлегию для выпуска газеты по решению задач на проценты с опубликованием общего эссе на сайте Dinkypage (ссылки на газету опубликованы на школьном сайте).
Мини-эссе "Проценты на Едином Государственном экзамене"
Поиск решения нестандартных задач является прекрасным средством развития критического мышления, строгости суждений и математического вкуса. Одним из таких средств является использование на уроках математики софизмов, примеров с поиском ошибок. Постановка проблемы – это главный метод, используемый мною на этом уроке. Он позволяет ученику самому проводить поиск решения, выбирать различные варианты, оценивать решения одноклассников. Приемы анализа и обобщения, рефлексия учащихся – это одна из основополагающих граней развития самоконтроля и самокритичности учеников, в то же время стимулирующая их на выработку собственного алгоритма решения задач с учетом применения того опыты и теории, которые они получают на уроке.
Результатом урока является изучение темы «Проценты» с помощью нахождения правильного решения задач, которые изначально представлены с ошибочными ответами. Уроки, проводимые в виде соревнований (с разделением учащихся на команды) всегда интересны для детей, подстегивают их желание проявить все свои возможности.
Использование компьютера и сетевых ресурсов делают процесс обучения более наглядным и современным, это позволяет ученикам проявить свои знания не только в области математики, но и информационных технологий, а для учителя упрощается процесс сбора результатов и значительно расширятся возможность предъявления учебной информации. Создание совместной газеты требует от учеников проявления творческих способностей. Наряду с пониманием математических аспектов данной темы, учащиеся видят насколько важно не только решить пример, но и грамотно его оформить и презентовать. Данный навык будет полезен для них и в дальнейшем обучении, так как в век развития информационных ресурсов человек не может отгородиться от их применения, более того это препятствует развитию его собственного потенциала. Компьютер – это не только средство развлечения и общения, это рабочий инструмент, с помощью которого можно значительно упростить взаимодействие людей и информации.
|