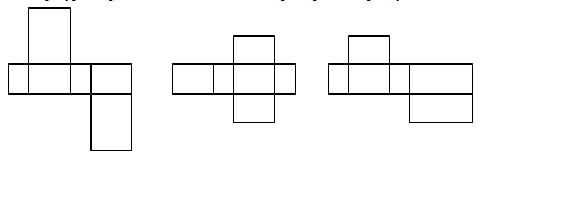Семинар ДООМ Развертки

Семинар ДООМ Развертки

Автор: Участник:Коннова Елена

Руководитель команд ДООМ 2009 Великие математики IDm082 и Многоугольник IDm083

Тип урока: формирование новых знаний.

Место урока: 5 класс, кружок

Форма проведения: Эвристическая беседа.

Цели урока:

-познакомить учащихся с понятием «развертка»

-научить строить различные развертки куба

-формирование исследовательских навыков учащихся

-развитие интереса к математике.

Необходимое оборудование:

- набор многогранников, развертки куба, прямоугольного параллелепипеда, призмы и пирамиды, сложенные в многогранники.

Ход урока:

1. Организационный момент.

1.Вступительное слово.

Мы с вами знаем названия некоторых многогранников : куб, параллелепипед, призма, пирамида. Оказывается, эти и многие другие фигуры можно сделать из бумаги. Сегодня мы научимся строить развертки куба и некоторых других фигур.

2. Решение задач.

1. Нарисуйте все фигуры тетрамино (фигуры, состоящие из 4 квадратиков).

2. Нарисуйте все фигуры пентамино (фигуры, состоящие из 5 квадратиков).

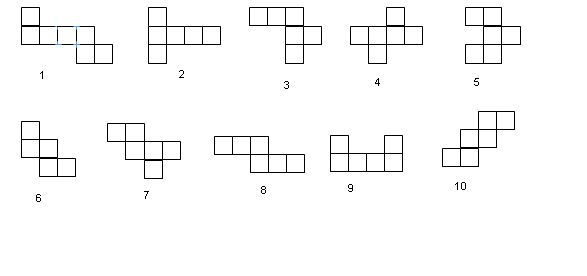
3. Какие фигуры, нарисованные ниже, являются развертками куба?

4. Нарисуйте все развертки куба. Сколько их?

5. Нарисуйте развертку прямоугольного параллелепипеда с измерениями 2, 3, 4.

6. Какие фигуры, нарисованные ниже, являются развертками прямоугольного параллелепипеда?

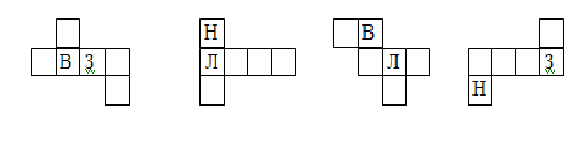
7. На каждой из нарисованных ниже разверток куба помечены две грани. Пометьте остальные грани так, чтобы после склейки развертки все надписи оказались снаружи куба. Отметьте стрелками ребра, которые нужно для этого склеить.

8. Какие пары граней в кубе не являются соседними, то есть не имеют общих ребер? Могут ли они быть соседними на развертке куба?

9. Верно ли утверждение: если две грани не являются соседними на развертке куба, то они не могут быть соседними и в самом кубе?

10. Найдите на поверхности куба путь наименьшей длины, соединяющий две противоположные вершины. Сколько таких путей?

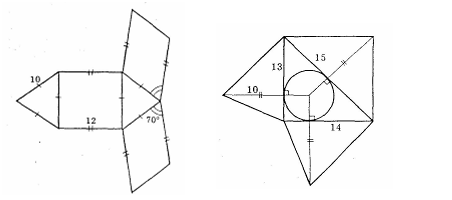
11. Нарисуйте развертки треугольной призмы.

12. Нарисуйте развертки треугольной пирамиды.

13. Нарисуйте развертки четырехугольной пирамиды.

Задание на дом: Склеить модели многогранников.

Использованы задачи Кировской летней школы и обучающего тура.

Дистанционный методический семинар ДООМ 2009 "Геометрическая геометрия"