Семинар ДООнк Логические задачи в олимпиадных работах по математике

Автор: Мартынова Оксана Валентиновна

Участник:Мартынова Оксана Валентиновна

Команда:ID-z037 Конфетти

Мир построен на силе чисел. Пифагор

Чему можно научить ребенка при обучении математике? Размышлять, объяснять получаемые результаты, сравнивать, наблюдать, обобщать и делать выводы. На развитие таких умений и навыков направлены предлагаемые олимпиадные задания для учащихся 2-4 классов. Их можно использовать как во время урока, осуществляя дифференцированный подход при обучении и контроле знаний учащихся, так и во внеклассной работе.

Олимпиада в начальный период обучения занимает важное место в развитии детей. Именно в это время происходят первые самостоятельные открытия ребенка. Пусть они даже небольшие и как будто незначительные, но в них - ростки будущего интереса к науке. Реализованные возможности действуют на ребенка развивающе, стимулируют интерес не только к математике, но и к другим наукам.

Олимпиады по математике — все более и более распространяющаяся форма математического соревнования для младших школьников.

Как готовиться к таким соревнованиям? Нужно ли проводить специальную подготовку к таким соревнованиям? Отбирать ли школьников для участия в таких соревнованиях? С какого класса можно проводить математические олимпиады? Не давая окончательных инструкций по всем этим вопросам, я попробую поделиться своим опытом работы с учащимися младших классов в этом направлении.

К концу первого года обучения в начальной школе накапливается достаточно материала для проведения олимпиады по математике. Уровень развития учащихся к этому моменту позволяет каждому ученику участвовать в такой олимпиаде, если он этого желает. Повторяю, что любой второклассник может участвовать в олимпиаде по математике, и эту возможность следует ему предоставить.

Содержание олимпиады для каждого года обучения должно соответствовать содержанию программы по математике этого года обучения.

Подготовка к математической олимпиаде начинается с работы на уроке. В содержание практически каждого урока должны входить или арифметические ребусы, или логические и комбинаторные задачи, или задания на разрезание и составление фигур, или другие упражнения на сообразительность. Работа на уроках математики дополняется занятиями математического кружка. Кружок проводится один раз в неделю, продолжительность занятия от 45 минут до 1 часа. Его посещают все учащиеся, желающие заниматься математикой. На кружке учащиеся обсуждают решения задач и получают на дом задания, которые разбираются на следующем занятии.

В течение учебного года можно проводить в классе, или на параллели нескольких классов, или с учащимися той же параллели других школ различные математические соревнования: математическую карусель, математический бой и т. д.

Логические задачи в курсе математики 2 класса требуют от учащихся внимательной работы с текстом. Условие такой задачи можно оформить в виде таблицы, с помощью которой учащиеся быстро приходят к правильному ответу на поставленный в задаче вопрос.

Приведу несколько примеров.

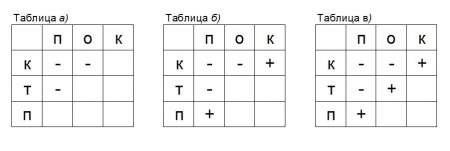
Задача 1. Три котенка — Касьянка, Том и Плут — съели плотвичку, окуня и карася. Касьянка не ел ни плотвичку, ни окуня. Том не ел плотвичку. Какую рыбку съел каждый котенок?

Решение: Составим таблицу, в которой строки обозначены именами персонажей задачи, а столбцы — названиями рыб, которых они съели.

Касьянка не ел ни плотвичку, ни окуня: в соответствующих клетках таблицы ставим «-». Том не ел плотвичку — в соответствующей клетке ставим «-» (табл. а).

Как видно из таблицы а), Касьянка мог съесть только карася, а плотвичку мог съесть только Плут: в соответствующих клетках таблицы ставим «+» (табл. б).

Следовательно, Том съел окуня: в соответствующей клетке таблицы ставим «+» (табл. в).

Задача 2. Трое друзей учатся в первом, втором и третьем классах. Их фамилии Иванов, Петров и Семенов. У самого младшего из друзей нет братьев и сестер. Семенов учится с сестрой Петрова в одном классе, он самый старший из друзей. Назови фамилии первоклассника, второклассника и третьеклассника.

Решение: При решении этой задачи не обязательно составлять таблицу. Достаточно внимательно прочитать текст. Семенов самый старший из друзей, следовательно, он учится в третьем классе. У самого младшего из друзей нет братьев и сестер, а у Петрова есть сестра, с которой Семенов учится в одном классе. Следовательно, самый младший из друзей — Иванов. Он учится в первом классе, а, значит, Петров учится во втором классе.

Такие задачи разбирались во втором классе. Их решения удавалось организовать в виде таблицы. В четвертом классе появляются задачи, в которых требуется проверить, какие из высказанных предположений соответствуют действительности. При этом мы сознательно не пользуемся терминологией доказательства от противного.

Задача 3. Рядом сидят мальчик и девочка. «Я мальчик», — говорит черноволосый ребенок. «Я девочка», — говорит рыжий ребенок. Какой цвет волос у мальчика и какой цвет волос у девочки, если известно, что хотя бы кто-то из них солгал?

Решение: Допустим, что черноволосый ребенок сказал правду: он мальчик. Тогда девочка рыжая. Получается, что рыжий ребенок тоже говорит правду. Но по условию кто-то из них солгал. Следовательно, черноволосый ребенок сказал неправду. На самом деле он девочка, а значит, рыжий ребенок мальчик.

Заметим, что слова «хотя бы кто-то из них солгал» означают, что солгал либо один ребенок, либо солгали оба. В нашей задаче сказали неправду оба ребенка.

Задача 4. Три класса участвовали в туристической эстафете. Один класс занял 1 место, другой — 2 место, а третий — 3 место. Перед началом соревнований болельщики заявили:

1) 4 «А» займет 1 место; 2) 4 «В» не займет 1 место; 3) 4 «Б» не будет последним. Одно из этих предположений оказалось верным, а два других — ошибочными. Какое место занял каждый из четвертых классов?

Решение: Допустим, что 1-е предположение оказалось верным: 1 место занял 4 «А». Тогда 2-е предположение «4 "В" не займет 1 место» тоже верно. Но по условию задачи оказалось верным только одно предположение. Следовательно, 1-е предположение на самом деле ошибочное: 4 «А» не занял 1 место.

Допустим, что 2-е предположение верно: 4 «В» не занял 1 место. Тогда 1 место остается за 4 «Б» и 3-е предположение «4 "Б" не будет последним» становится тоже верным. Но по условию задачи только одно предположение должно быть верным, значит, 2-е утверждение на самом деле ошибочно. Таким образом, 1-е и 2-е предположения оказались ошибочными. Следовательно, 3-е предположение верно: 4 «Б» не был последним. На самом деле, 4 «В» занял первое место, 4 «Б» — второе, а 4 «А» досталось третье место.

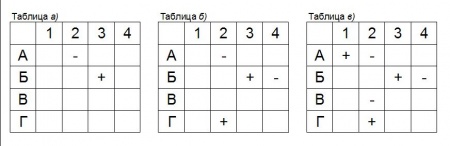
Задача 5. Четверо друзей соревновались в запуске на дальность бумажных самолетиков. Один из них занял 1 место, другой — 2 место, третий — 3 место и четвертый — 4 место. На вопрос, какое каждый из них занял место, они ответили:

Андрей: Я был вторым, Боря — третьим. Вася: Я был вторым, Андрей — первым. Гриша: Я был вторым, Боря — четвертым.

При этом известно, что каждый мальчик один раз говорил правду, а один раз — неправду. Кто какое место занял?

Решение: Допустим, что Андрей первый раз сказал правду: он занял 2 место, а второй раз сказал неправду: Боря не был третьим. Тогда Вася первый раз солгал: он не был вторым, а второй раз сказал правду: Андрей был первым. Но Андрей занять сразу 1 и 2 место не мог, следовательно, Андрей первый раз солгал, а второй раз сказал правду. На самом деле он не занял 2 место, а Боря действительно занял третье место.

Начинаем заполнять таблицу а).

Боря занял, как мы установили, 3 место, поэтому утверждение Гриши «Боря был четвертым» — неправда, а его утверждение «Я был вторым» — правда (табл. б).

Утверждение Васи «Я был вторым» — ложь, а его утверждение «Андрей был первым» — правда.

Следовательно, сам Вася был четвертым (табл. в).

Задача 6. Три друга учатся в гимназии. Один из них в математическом, другой — в физическом и третий — в биологическом классах. При этом известно:

Если Петр математик, то Сергей не физик.

Если Роман не физик, то Петр математик.

Если Сергей не математик, то Роман биолог.

Определи специальность каждого.

Решение: Из условия следует такая последовательность утверждений: Петр математик => Сергей не физик => Сергей биолог => Сергей не математик => Роман биолог. Но друзья учатся в разных классах. Следовательно, на самом деле Петр не математик.

Теперь выстраивается такая последовательность верных утверждений: Петр не математик => Роман физик => => Сергей математик => Петр биолог.

В настоящее время в обществе сложилось новое понимание основной цели образования. Учитель в первую очередь должен заботиться о формировании у ученика способности к саморазвитию, которая обеспечит интеграцию личности в национальную и мировую культуру.

Помочь учащимся в полной мере проявить свои способности, развить инициативу, самостоятельность, творческий потенциал - одна из основных задач современной школы.

Реализовать эту задачу можно, если формировать у них познавательные интересы средствами занимательности, тесно связанными с изучаемым материалом и врожденной любознательностью младших школьников.

Используемая литература:

1. Дьячкова Г.Т. Математика. 2-4 классы: олимпиадные задания.,- Волгоград, изд-во «Учитель» 2008 год.

2. Гейдман Б.П. и др. Подготовка к математической олимпиаде. Начальная школа. 2-4 классы.,- Москва, изд-во «АЙРИС- пресс», 2007 год.

3. Жильцова Т.В. и др. Поручные разработки по наглядной геометрии: 1-4 класс.,- Москва, изд-во «ВАКО», 2004 год.