Как изображаются комбинаций сферы и многогранников?

Для изображения сферы используется ортогональное проектирование.

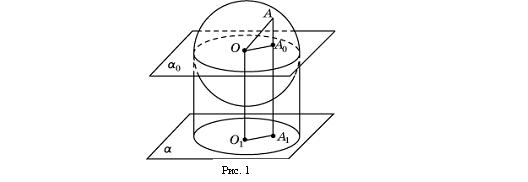
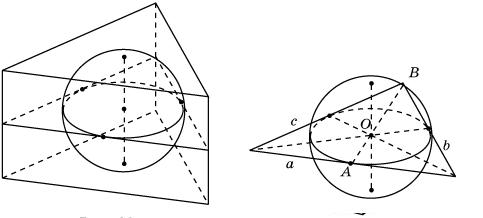
Теорема. Ортогональной проекцией сферы является круг, радиус которого равен радиусу сферы. Доказательство. Проведем плоскость a0, проходящую через центр сферы О и параллельную плоскости проектирования a. Поскольку плоскости a и a0 параллельны, то проекции сферы на эти плоскости будут равны (рис. 1). Сечением сферы плоскостью a0 является окружность радиуса R, равного радиусу сферы. Если А точка сферы, не принадлежащая этой окружности, и А0 ее ортогональная проекция на плоскость a0, то ОА0 < OA R. Таким образом, при ортогональном проектировании на плоскость a0 точки этой окружности остаются на месте, а остальные точки сферы проектируются внутрь соответствующего круга. Следовательно, ортогональной проекцией сферы является круг того же радиуса.

Для большей наглядности изображения сферы в ней выделяют большую окружность (сечение сферы плоскостью, проходящей через ее центр), плоскость которой образует острый угол с направлением проектирования, и полюсы (концы диаметра, перпендикулярного плоскости большой окружности). Большая окружность называется экватором. Окружности, лежащие в плоскостях, параллельных плоскости экватора - параллелями, прямая, проходящая через полюсы – осью, а большие окружности, проходящие через полюсы – меридианами.

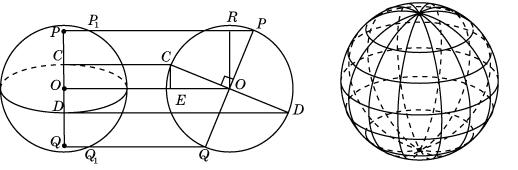
Проекцией выделенной большой окружности будет эллипс. Для нахождения изображения полюсов будем считать исходную ортогональную проекцию видом сферы спереди, и построим вид сферы слева, т. е. ортогональную проекцию сферы на плоскость, проходящую через ось сферы и перпендикулярную плоскости проектирования. Большая окружность и ось сферы изобразятся перпендикулярными диаметрами PQ и CD (рис. 2). Изображение полюсов на основной плоскости получается параллельным переносом полюсов на виде сферы слева.

На практике можно не прибегать к построению вспомогательного чертежа (вида сферы слева). Для построения изображения полюсов P и Q достаточно заметить, что прямоугольные треугольники OPR и OCE равны (по гипотенузе и острому углу). Следовательно, имеет место равенство отрезков RP = CE. Кроме того, имеем RP = PP1 и CE = OC. Значит PP1 = OC. Аналогично, QQ1 = OD. После этого точки P и Q выбираются так, чтобы выполнялись эти равенства.

На изображении сферы, помимо экватора и полюсов, можно нарисовать несколько параллелей и меридианов (рис. 3).

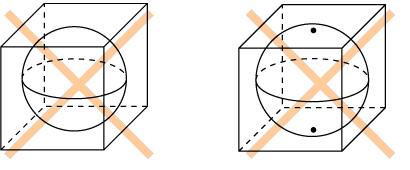
Рассмотрим теперь вопрос об изображении комбинаций многогранников и тел вращения. Начнем с куба и сферы. Одной из распространенных ошибок изображения сферы, вписанной в куб, является изображение, показанное на рисунке 4. Здесь сразу несколько ошибок. Первая связана с неверным изображением точек касания. Точки касания должны располагаться не на окружности, ограничивающей изображение сферы, а внутри нее. Так, например, точки касания верхней и нижней граней куба должны располагаться в полюсах сферы. Эту ошибку можно исправить, несколько увеличив размеры вписанной сферы, как показано на рисунке 5. Здесь как будто точки касания верхней и нижней граней куба расположены в полюсах сферы, однако это изображение также не является верным. Ошибка рисунков 4 и 5 состоит в том, что для изображения сферы и куба использованы разные проекции. Сфера изображена в ортогональной проекции, а куб нет. На одном изображении этого делать нельзя. Если сфера изображается в ортогональной проекции, то и куб должен изображаться в ортогональной проекции.

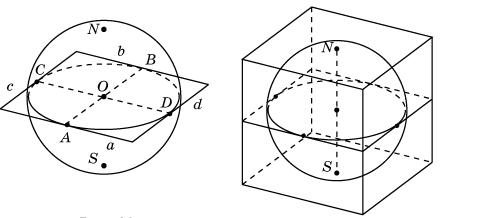
Для построения правильного изображения сферы, вписанной в куб, сначала изобразим сферу с экватором и полюсами (рис.6). Затем опишем около экватора квадрат и построим его изображение. Это можно сделать следующим образом. Отметим на эллипсе, изображающем экватор какую-нибудь точку A и проведем касательную a к эллипсу в этой точке. Через точку A и центр эллипса O проведем прямую, и ее точку пересечения с эллипсом обозначим B. Через точку B проведем прямую b, параллельную a. Она также будет касательной к эллипсу. Построим диаметр CD, сопряженный диаметру AB эллипса и через точки C и D проведем прямые c и d, параллельные AB. Они будут касательными к эллипсу. Параллелограмм PQRS будет искомым изображением квадрата, описанного около экватора.

Через вершины параллелограмма проведем прямые, параллельные оси SN сферы и отложим на них в обе стороны отрезки, равные ON = OS. Получим вершины верхнего и нижнего оснований куба, описанного около сферы. Соединяя теперь соответствующие вершины верхнего и нижнего оснований, получим остальные ребра искомого куба (рис. 7).

Заметим, что изображение куба, описанного около данной сферы, полностью определяется начальным выбором точки A. Выбирая различным образом эту точку можно получать различные изображения куба, описанного около сферы.

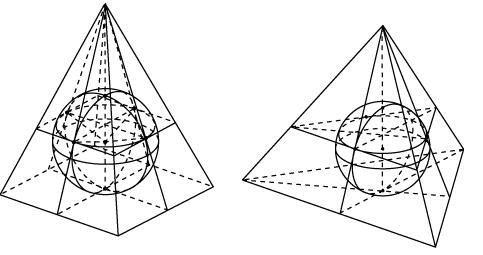
Аналогичным образом строится изображение правильной треугольной призмы, описанной около сферы (рис. 8). Сначала строим изображение правильного треугольника, описанного около экватора. Для этого выбираем точку касания A и проводим через нее касательную a. Через точку A и центр эллипса проводим прямую и откладываем на ней отрезок OB = 2OA. Через точку B проводим касательные b и c к эллипсу. Прямые a, b и c образуют искомый треугольник, описанный около эллипса (рис. 9). Через вершины этого треугольника проведем прямые, параллельные оси SN сферы и отложим на них в обе стороны отрезки, равные ON = OS. Получим вершины верхнего и нижнего оснований призмы, описанной около сферы. Соединяя теперь соответствующие вершины верхнего и нижнего оснований, получим остальные ребра искомой призмы (рис. 8).

Аналогичным образом строится изображение пирамиды с вписанной в нее сферой (рис. 10). В случае, если сфера вписана в правильный тетраэдр (рис. 11), нужно учитывать, что центр сферы делит высоту пирамиды в отношении 3:1 считая от вершины.

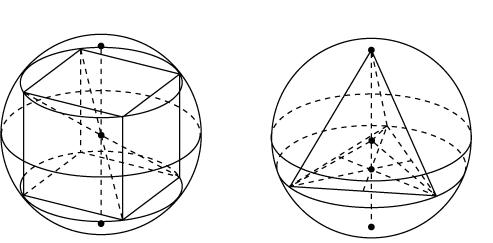
На рисунках 12 изображена сфера с вписанным в нее кубом. На рисунке 13 изображена сфера с вписанным в нее правильным тетраэдром.