Копилка знаменитых задач продолжение
Посмотреть страницу Копилка знаменитых задач.
Уважаемые участники! Страница заполнена, продолжение на странице Копилка знаменитых задач продолжение 3.
Задачи участников ДООМ
ЛАДА-ВЕКТОР ID 279
1. Задача индийского математика XII в. Бхаскары.
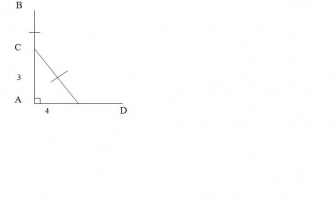
На берегу реки рос тополь одинокий. Вдруг порыв ветра его ствол надломил. Бедный тополь упал. И угол прямой с теченьем реки его ствол составлял. Запомни теперь, что в том месте река в четыре лишь фута была широка. Верхушка склонилась у края реки. Осталось три фута всего от ствола. Прошу тебя, скоро теперь мне скажи: У тополя как велика высота?
Решение:
Дано:
треугольник ACD – прямоугольный,
АС = 3 фута,
AD = 4 фута.
Найти: АВ.
Решение:
АВ = АС + СD; ВС = СD;
CD 2 = AC x2 + AD x2 (по теореме Пифагора),
CD x2 = 3 x2 + 4 x2, CD x2 = 25, CD = 5 (Ф);
АВ = 3+5 = 8 (Ф).
1 фут (1 Ф) ~ 30,5 см.
Ответ: 8 футов или ~ 244 см.
2.Решение древнекитайской задачи
В клетке находятся фазаны и кролики. Известно, что у них 35 голов и 94 ноги. Узнайте число фазанов и число кроликов.
Решение:
I способ Так решали в древнем Китае.
Представим, что наверх клетки, в которой сидят фазаны и кролики, мы положим морковь. Все кролики встанут на задние лапки, чтобы дотянуться до моркови!
1) Сколько ног в этот момент будет стоять на земле?
35 2=70 (ног).
2) Но в условии даны 94 ноги, где же остальные? Это передние лапы кроликов:
94 – 70= 24.
3) Сколько же кроликов?
24: 2 = 12.
4) Сколько фазанов?
35 – 12 = 23.
Ответ: 12 кроликов и 23 фазана.
II способ решения:
Пусть х – число фазанов, у – число кроликов. Всего у них 35 голов и 94 ноги. Значит,
х + у = 35
2х + 4у = 94. Умножим все члены уравнения на 2 и вычтем первое уравнение из второго.
2х + 2у = 70
2х + 4у = 94
2у = 24
у = 12
В клетке было 12 кроликов.
х = 35 – у
х = 23
Было 23 фазана.
Ответ: 23 фазана и 12 кроликов.
3. Задача на применение теоремы Пифагора (Арабский математик XI век)
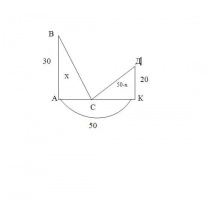
На обоих берегах реки растет по пальме, одна против другой. Высота одной-30 локтей, другой -20 локтей; расстояние между их основаниями- 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, всплывшую к поверхности воды между пальмами; обе кинулись к ней разом и достигли её одновременно. На каком расстоянии от основания более высокой пальмы появилась рыба?
Решение:
Расстояние от основания более высокой пальмы до места появления рыбы, обозначим основания х. тогда расстояние до более низкой пальмы (50-х) локтей, т.к. известно расстояние между ними – 50 локтей.
Рассмотрим прямоугольные треугольники: ABC и KDC.
АВ= 30 локтей, КД= 20 локтей, АС= х локтей, КС=(50-х) локтей, ВС=ДС, т.к. птицы достигли рыбы одновременно.
Применяя теорему Пифагора.
АВ x2 +АС x2 = ВС x2 и КД x2 +КС x2 =ДС x2, т.к. ВС=ДС, то ВС x2 =КД x2 +КС; x2 30 x2 +х =20 x2 +(50-х) x2; 900+х x2 =400+2500-100х+х x2; х=20 Ответ: 20 локтей.
4.Задача на числа (Диофант, III в.)
Найдите 2 числа, зная, что их сумма равна 20, а произведение 96.
1 способ решения:
Первое число обозначим х, второе у и составим систему уравнений; т.к. сумма чисел равна 20, то: х + у = 20; произведение 96, то х у = 96, т.е
Используя т.Виета:
х = 12; у = 8 или х =18; у = 12.
Ответ: 8 и 12.
2 способ решения:
Первое число обозначим х, второе (20-х), т.к. сумма чисел равна 20. Зная их произведение, составим уравнение:
х (20-х) = 96; х -20х+ 96 = 0
Используя т.Виета:
х=8
х=12.
Ответ: 8 и 12.
5.Задача на дроби (Бхаскары; Индия,XII в.)
Из множества чистых цветков лотоса были принесены в жертвы: Шиве- 3 доля этого множества; Вишну-пятая и Солнца- шестая; четвертую долю получил Бхавани, а остальные шесть цветков получил уважаемый учитель. Сколько было цветков?
Решение:
Пусть всего цветов было х.
Шива получил третью долю из всего множества, т. е. 1х/4.
Зная, что ещё цветков получил уважаемый учитель, составим уравнение:
6.Задача на составление системы уравнений (Старинная задача).
Лошадь вместе с седлом стоит 235 рублей; лошадь же вместе со с рубей стоит 250 рублей; сбруя же с седлом стоит 135 рублей. Что стоит лошадь, что седло, что сбруя?
Решение:
Решим задачу с помощью системы уравнений. Пусть х
Возьмём за х рублей стоимость лошади, у рублей – сёдла, я рублей – сбруи. По условию:
x+y=235;
x+y=250;
y+z=135;
Вычитаем из первого уравнения второе:
x+y-x-z=235-250;
y=z-15;
Подставим полученное выражение в третье уравнение:
z-15+z=135;
z=75;
Найдём у:
у = z- 15=75-15=60;
Найдём х:
х + 60=235;
х=175.
Ответ: 175 рублей, 60 рублей, 75 рублей.
7.Вознаграждение воина.
Задача из «Полного курс чистой математики , сочиненный Артиллерии Штык-Юнкером и Математики партикулярным Учителем Ефимом Войтяховским в пользу и употребление юношества и упражняющихся в Математике» (1795г)
Служившему воину дано вознаграждение за первую рану 1 копейка, за другую -2 копейки, за третью – 4 копейки и т.д. По исчислению нашлось , что воин получил всего вознаграждения 655 руб. 35 коп. Спрашивается число его ран.
9. Задача Эйлера
Две крестьянки принесли на рынок вместе 100 яиц, одна больше, нежели другая; обе выручили одинаковые суммы. Первая сказала тогда второй: «Будь у меня твои яйца, я выручила бы 15 крейцеров». Вторая ответила: «А будь твой яйца у меня, я выручила бы за них крейцера». Сколько яиц у каждой?
РЕШЕНИЕ
I способ:
Пусть у первой крестьянки x яиц, тогда у второй 100 – x. Если бы первая имела 100 – x яиц, она выручила бы, мы знаем 15 крейцеров. Значит, первая крестьянка продала яйца по цене
Отрицательный корень в данном случае не имеет смысла; у задачи – только одно решение: первая крестьянка принесла 40 яиц и , значит, вторая 60. II способ: Предположим, что вторая крестьянка имела в k раз больше яиц, чем первая. Выручили они одинаковые суммы; это значит, что первая крестьянка продавала свои яйца в k раз дороже , чем вторая. Если бы перед торговлей они поменялись яйцами , то первая крестьянка имела бы в k раз больше яиц , чем вторая , и продавала бы их в k раз дороже. Это значит ,что она выручила бы в k больше денег, чем вторая. Следовательно, имеем:
10. Покупка лошади
Задача из «Арифметики» Магницкого.
Некто продал лошадь за 156 руб. Но покупатель, приобретая лошадь, раздумал её покупать и возвратил продавцу, говоря - Нет мне расчёта покупать за эту цену лошадь, которая таких денег не стоит тогда продавец предложил другие условия. Если, по-твоему цена лошади высока, то купи только её подковные гвозди, лошадь же получишь тогда в придачу бесплатно. Гвоздей в каждой подкове 6. За первый гвоздь дай мне всего ¼ коп., за второй – ½ коп., за третий – 1 коп. и т.д. Покупатель соблазнённый низкой ценой и желая даром получить лошадь, принял условия продавца, рассчитывая, что за гвозди придётся уплатить не более 10 рублей. На сколько покупатель проторговался?
Решение
12. Задача Л. Эйлера.
Некий чиновник купил лошадей и быков за 1770 талеров. За каждую лошадь он уплатил по 31 талеру, а за каждого быка — по 21 талеру. Сколько лошадей и быков купил чиновник? Здесь неизвестно общее число купленных животных, по¬этому не удастся составить уравнение с одной переменной или систему уравнений с двумя переменными. Пусть чиновник купил х лошадей и у быков. Тогда 31х + 21у=1770.
По смыслу задачи х и у — натуральные числа. Так как 21 и 1770 делятся на 3, то 31 х делится на 3 и х: делится на 3: х = 3х1, где х1 — натуральное число. Тогда 31х1 +21y=1770
13. Задача Л. Пизанского (Фибоначчи)
Некто купил 30 птиц за 30 монет, из числа этих птиц за каждых трех воробьев заплачена 1 монета, за каждые две горлицы - также 1 монета и, наконец, за каждого голубя - по 2 монеты. Сколько было птиц каждой породы?
Пусть купили х воробьев, у горлиц, тогда купили 30-х-у - голубей. Здесь х и у - натуральные числа. Составим уравнение:
1/3х+1/2y+2(30-x-y)=30
Умножим правую и левую части уравнения на 6:
2х + 3у + 12 (30 — х — у) = 180.
После упрощения получим: 10х+9у=180
Применим показанный выше метод понижения коэффициентов. Так как у делится на 10, то у=10у1, где у1-на число.
Подставим 10у вместо у в уравнение (4) и упростим его: х + 9 у1 = 18.
Так как х делится на 9, то х = 9х1, где х1 - - натуральное число. Подставим 9х1 вместо х в уравнение (5) и упростим его: Х1 + у1=2
Это уравнение имеет единственное решение в натуральных числах: Х1= 1 ; у1 = 1, по которому, пользуясь форм х = 9 Х1 и у=10 у1, найдем решения уравнений (4) и х = 9, у=10. Итак, на 30 монет купили 9 воробьев, 10 горлиц и 11 голубей.
14. Задача из «Всеобщей арифметики» И. Ньютона.
Коровы на лугу.
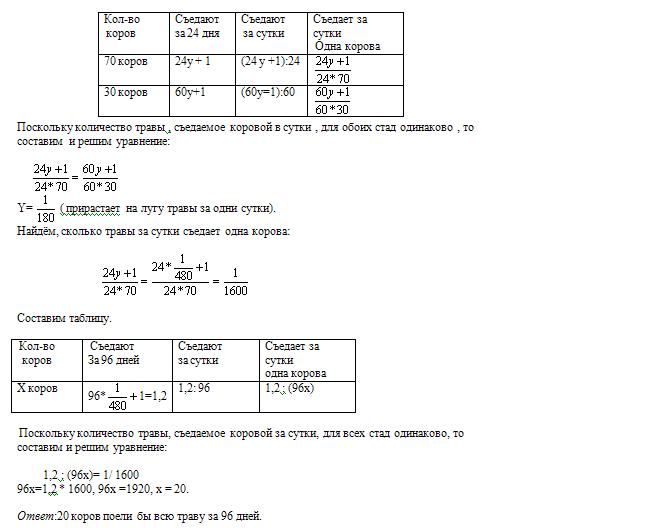
Трава на всём лугу растёт одинаково густо и быстро. Известно , что 70 коров поели бы её в 24 дня, а 30 коров – в 60 дней. Сколько коров поели бы всю траву луга в 96 дней.
При обсуждении этой задачи ребята , как правило , всегда ошибочно излагают ход решения , не учитывая, что трава всё время растёт , и в итоге приходят к нелепым ответам.
Решение.
Введём вспомогательное неизвестное. Пусть в сутки прирастает y травы, общий запас примем за 1, а количество коров обозначим за x .
Составим таблицу.
--Лада-Вектор ID 279 15:40, 24 октября 2008 (SAMST)
--Сталкера задач ID 219 16:11, 24 октября 2008 (SAMST)
Задача 1.
Вопросил некто некоего учителя: "Сколько имеешь учеников у себя,так как хочу отдать сына к тебе в училище". Учитель ответил: "Если ко мне придет учеников еще столько же, сколько имею, и полстолько, и четвертая часть, и твой сын, тогда будет у меня учеников 100." Сколько было у учителя учеников?
Решение:
2х+1/2*х+1/4*х+1=100, х=36
Ответ: 36 учеников.
Задача 2.
Посеял мужик репу на квадратном огороде, периметр которого 100 сажень. Проведал про то медведь, говорит:
- Половину урожая - мне, не то - задеру.
Нечего делать, отделил мужик от своего огорода квадратный участок с вдвое меньшим периметром.
- Вот, - говорит медведю, - тут твоя репа будет расти.
Поспела репа. Надергал медведь со своего участка 6 сотен репок.
Сколько реп мужику досталось?
Решение:
У мужика участок со стороной 25 сажень. Площадь была 625.
У медведя - со стороной 12,5 сажень, площадью - 625/4
Мужик должен был собрать 24 сотни, но 6 сотен собрал медведь.
Ответ: 18 сотен
Задача 3.
Пятая часть пчелиного роя сидит на цветках жасмина, одна треть — на цветках гиацинта.
Утроенная разность последних двух чисел пчел отправились к цветкам роз.
Только одна пчелка летала взад-вперед, не находя себе места.
Скажи мне, сколько всего пчел?
Решение:
Число пчел должно делиться на 3 и на 5.
Ответ: 15
Задача 4.
Молочница торговала молоком из бочки и маленького бочонка, который вмещал втрое меньше молока,чем бочка.
Когда в бочке осталось 39 л молока, а в бочонке — 21л, она долила его молоком из большой бочки.
В результате большая бочка оказалась наполненной ровно наполовину.
Какого объема была бочка?
Решение:
Задача решается уравнением. Объем боченка примем за х, а бочки - 3х.Долили в боченок х-21, т.е. в большой осталось 39 - (х - 21) или 1,5х
Ответ: 72 литра
Задача 5.
У Маши на девяти карточках написано девять цифр: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Она пытается составить из них три трехзначных числа, которые были бы пропорциональны числам 1; 3 и 5, но что-то эта затея у Маши не получается.
Тут пришел Миша и сказал:
— Я знаю, одно число кончается так: ...87.
— Не подсказывай больше! — воскликнула Маша. — Я теперь сама сделаю!
А вы сумеете решить сами?
Решение:
В рассуждении необходимо учесть, что одно число должно делиться на 3, а другое - на 5. Значит одно число заканчивается цифрой 5, а одно из предыдущих - нечетной цифрой.
Ответ: 129, 387, 645.
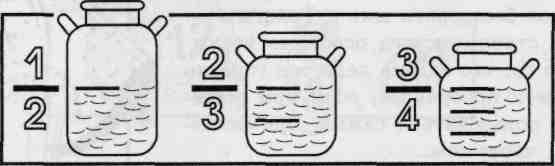
Задача 6.
Каждый из трех бидонов вмещает целое число литров воды. Бидоны заполнили одинаковым количеством воды, при этом первый бидон
был наполнен на 1/2 своего объема, второй — на 2/3 своего объема, а третий — на 3/4 своего объема.
При каких наименьших объемах бидонов возможна такая ситуация?
1/2*х=2/3*у=3/4*z или 6х=8у=9z.
Ответ: 12л, 9л, 8л.
Задача 7.
Хрюша — именинник. У него — кулек конфет. Вначале он сунул 2 конфетки нетерпеливой Каркуше, чтоб отвязалась, потом отложил 5 штук себе, чтоб не забыть. Степашке дал среднее арифметическое числа конфет, выданных Каркуше и себе, Филе — среднее арифметическое числа конфет, данных Каркуше, себе и Степашке, следующему гостю — среднее арифметическое числа конфет, данных Каркуше, себе, Степашке и Филе, и т.д. Как раз хватило всем. В конце праздника Хрюша решил стать справедливым и от своих конфет отделил часть гостю, получившему меньше всех. Кому и сколько конфет отделил Хрюша?
Решение:
Каркуша получила 2 штуки, Хрюша - 5, Степашка - (2+5):2=3,5, Филя - (2+5+3,5):3=3,5, гость - (2+5+3,5+3,5):4=3,5. Т,е каждый получил по 3,5 конфеты кроме Каркуши.
Ответ: Каркуше 1,5 штуки
--Сталкер 14:00, 25 октября 2008 (SAMST)
ЗВЕЗДА ID 248
ЗАДАЧИ РАЗНЫХ СТРАН
Задача №1 РОССИЯ
На вопрос о том, сколько времени, был дан такой ответ: «Две пятых времени, прошедшего от полуночи до этого момента, равно двум третьим времени, которое осталось до полудня». Сколько сейчас времени?
Решение
От полуночи до полудня 12 часов, если t ч. — время, прошед¬шее от полуночи до настоящего времени, то:
2 / 3t = 2 / 3(12 − t)
Следовательно, в данный момент t = 7,5 ч., т.е. часы показы¬вают 7 ч. 30 мин. Ответ: 7 ч. 30 мин.
Задача №2 ФРАНЦИЯ
Чему равно наименьшее число, которое при делении на 2, 3, 4, 5, 6 дает в остатке 1, 2, 3, 4, 5 соответственно.
Решение:
Пусть п - неизвестное число. Так как при делении п на 2 в остатке 1, значит, (п + 1) делится на 2 без остатка. Если п при делении на 3 дает в остатке 2, то число (п + 1) делится на 3 без остатка и т.д. Наименьшее кратное 2, 3, 4, 5, 6 равно 60. Сле¬довательно, п = 60 -1 = 59.
Ответ: 59.
Задача №3
Когда у старушки Леони спрашивают, сколько у нее кошек, она меланхолично отвечает: «Четыре пятых моих кошек плюс четыре пятых кошки». Сколько же у Леони кошек?
Решение:
Пусть п - число кошек у Леони. Со слов старушки можем записать уравнение:
4 4 — n + - = n 5 5
n = 4
Ответ: 4 кошки.
Задача №4 БОЛГАРИЯ
Отец, по имени Николай, с сыном и отец, по имени Петр, с сы¬ном отправились удить рыбу. Число рыб, пойманных Николаем, оканчивается на 2, а число рыб, пойманных его сыном - на 3; число рыб, пойманных Петром, также оканчивается на 3, а число рыб, пойманных его сыном - на 4. Число рыб, пойманных на¬шими рыболовами вместе, совпадает с квадратом некоторого натурального числа. Как зовут сына Николая?
Решение:
Так как сумма последних цифр 2 + 3 + 3 + 4 = 12 оканчива¬ется на 2, и не существует квадрата натурального числа, который оканчивается на 2, то речь идет не о четырех, а лишь о трех ры¬баках, т.е. сын одного из любителей рыбной ловли одновременно является отцом другого (2 + 3 + 4 = 9). Николай не может быть сыном Петра, т.к. улов Николая оканчивается на 2, а не на 4, как того требует условие задачи. Следовательно, Петр - сын Николая.
Ответ: Петр.
Задача №5 ДАНИЯ
Рыбаки Адам, Бауэр, Кристиансен и Дазе (сокращенно: А, Б, К, Д), взвесив свой улов, установили следующее:
1) Д поймал больше, чем К; 2) А и Б вместе поймали столько же, сколько К и Д вместе; 3) А и Д вместе поймали меньше, чем Б а К вместе. Расположите результаты взвешиваний уловов а, б, к, д рыба¬ков А, Б, К, Д по величине.
Решение:
Результаты взвешивания улов а, б, к, д удовлетворяют соот¬ношениям: к<д (1)
а + б = к + д (2)
а + д < б + к (3)
Из (2) и (3) при сложении получим неравенство:
2а + б + д < б + 2к + д
2а < 2к
а < к (4)
Из (1) и (4) следует, что а < к < д.
Из (2) и (4) получим д < б. Значит, выполняется цепочка не¬равенств: а < к < д < б. Значит, самый большой улов у Бауэра, за ним у Дазе, Кристиансена и Адама.
Задача №6 АВСТРАЛИЯ
Скотовод завещал трем своим сыновьям Альфреду, Джону и Чарльзу разделить стадо овец следующим образом: Альфред получит на 20% больше Джона и на 25% больше Чарльза. Часть Джона - 3600 овец. Сколько овец получит Чарльз?
Решение:
Альфред получит 3600 + 0,2 • 3600 = 4320 овец. Это число на 25% больше z - числа овец Чарльза, т.е.
4320 = z - 0,25z
z = 3456
Ответ: 3456 овец получит Чарльз.
Задача №7 ЧЕХИЯ
По преданию, основательница чешского государства принцес¬са Либуша обещала отдать свою руку тому из трех женихов, кто сумеет решить задачу: «Если бы я дала первому жениху половину слив из этой корзины и еще одну сливу, второму жениху - поло¬вину оставшихся слив и еще одну сливу, а оставшиеся сливы поделила пополам и половину их и еще три сливы дала бы треть¬ему жениху, то корзина бы опустела». Сколько слив в корзине?
Ответ: 22 сливы.
Задача №8 Германия
Сын спросил отца, сколько ему лет. Отец ответил так: «Если прибавить к моим годам их половину, затем их четверть и еще один год, то получится 134 года». Сколько отцу лет?
Решение:
Пусть отцу х лет, тогда по условию задачи:
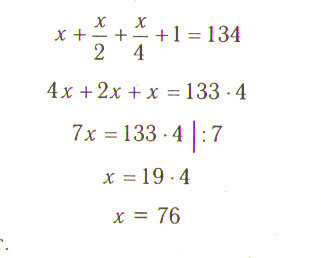
Ответ:76 лет
Задача №9
За какое время лев, волк и собака могут съесть трех овец, если лев один может съесть овцу за 1 час, волк - за 3 часа, а со¬бака - за 6 часов.
Решение:
Если t ч. - время, за которое все трое могут съесть одну овцу, то съеденные части соответственно равны
t/1; t/3; t/6. Из равенства
t/1+t/3+t/6= 1 находим t = 2/3 часа, т.е. 40 мин. Следовательно, все трое съедят трех овец за 40x3=120 мин., т.е. за 2 часа.
Ответ: 2 часа.
Задача №10 Жизнь Диофанта
(наглядно-геометрический способ)алгебраический у команды
Прах Диофанта гробница покоит: дивись ей –
И камень мудрым искусством его скажет успокоившего век.
Волей богов шестую часть жизни он прожил ребенком
И половину шестой встретил с пушком на щеках.
Только минула седьмая, с подругою он обручился.
С нею пять лет проведя, сына дождался мудрец.
Только полжизни отцовской возлюбленный сын его прожил,
Отнят он был у отца ранней могилою своей.
Дважды два года родитель оплакивал тяжкое горе.
Тут и увидел предел жизни печальной своей.
Сколько лет прожил Диофант?
Решение
Наглядно-геометрический способ 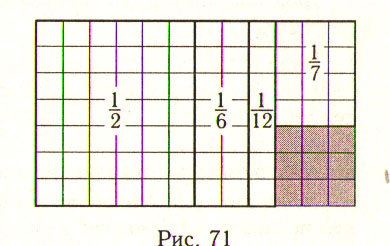
Так как в задаче речь идет о 1/6, 1/12, 1/7 и 1/2 частях жиз¬ни, то число лет, прожитых Дио¬фантом, надо делить на 6, 12, 7 и 2. Изобразим всю жизнь Диофанта в виде прямоуголь¬ника размером 7x12 клеток. Тогда 1/6, 1/12 и 1/2 части жиз¬ни изобразить легко; 1/7 - это полоска размером 1x12, т.е. 12 клеток, значит 1/7 жизни можно изобразить, например, прямоугольником 3x4 клетки. Оставшая¬ся затемненная часть соответствует 9 годам жизни Диофанта (4 + 5 = 9). Итак, одна клетка соответствует одному году жизни, всего получится 7х2 =84 клетки. Способ подбора Число лет Диофанта делится на 6, 12, 7 и 2.
--ЗВЕЗДА ID 248--ЗВЕЗДА ID 248 16:55, 24 октября 2008 (SAMST)
Участник:Совокупность "жареных семечек"ID-224
Задача №1 Продажа сапогов со скидкой.
Сапожник сделал сапоги и сказал подмастерью продать их за 25 рублей. К подмастерью на рынке подошло двое инвалидов (у одного нет левой ноги, у другого - правой), и он продал им по сапогу за 12,50 соотвественно. Возвращается, отдает деньги сапожнику и рассказывает, как удачно продал… А сапожник отвечает: “ну что ж ты, инвалидам надо было сделать скидку. Держи 5 рублей, разыщи их и верни по 2,50″ А подмастерье решил отдать инвалидам только по рублю, а остальные три рубля пропил. Нашел инвалидов и отдал каждому по рублю. Вышло, что сапоги обошлись инвалидам по 11,50. 11,50+11,50 = 23 и еще 3 рубля пропиты. Итого: 26 рублей, а было 25. Откуда лишний рубль?
Ответ на задачу 1.
3 рубля, пропитых подмастерьем, уже входят в 23 рубля, заплаченных инвалидами за сапоги. Поэтому их нельзя складывать, как это сделано в условиях задачи. Сапожник получил за сапоги 25 рублей, затем 5 рублей велел отдать инвалидам. Значит у сапожника осталось 20 рублей. Получается, инвалиды, получив обратно по рублю, заплатили за сапоги 23 рубля, из которых 20 рублей досталось сапожнику, а 3 рубля пропил подмастерье. Никаких “лишних” денег в сделке не возникло.
Задача №2 Воз сена
Лошадь съедает воз сена за месяц, коза за два месяца, овца за три месяца. За какое время лошадь, коза и овца вместе съедят такой же воз сена?
Решение.
Поскольку лошадь съедает воз сена за месяц, то за год (12 месяцев) она съест 12 возов сена. Так как коза съедает воз сена за два месяца, то за год она съест 6 возов сена. И наконец, поскольку овца съедает воз сена за 3 месяца, то за год она съест 4 воза сена. Вместе же они съедят за год 12 + 6 + 4 = 22 воза сена. Тогда один воз сена они все вместе съедят за месяца.
Задача №3 Основание Карфагена.
Об основании города Карфагена существует древнее предание. Дидона, дочь тирского царя, потеряв мужа, убитого ее братом, бежала в Африку. Там она купила у нумидийского царя столько земли, "сколько занимает воловья шкура". Когда сделка состоялась, Дидона разрезала воловью шкуру на тонкие ремешки и благодаря такой уловке охватила участок земли, достаточный для сооружения крепости. Так будто бы возникла крепость Карфаген, а впоследствии был построен и город. Попробуйте приблизительно определить, какую площадь могла, согласно этому преданию, занять крепость, если считать, что размер воловьей шкуры 4 кв. м., а ширина ремешков, на которые Дидона ее разрезала, 1 мм.
Ответ:
Если площадь воловьей шкуры 4 кв. м. (или 4 млн. кв. мм.), а ширина ремешков 1 мм., то общая длина вырезанного ремня (Дидона, надо думать, вырезала его спирально) - 4 миллиона миллиметров, или 4000 метров, т.е. 4 км. Таким ремнем можно окружить квадратный участок 1 кв. км. и круглый - в 1,3 кв. км.
Задача №4 Любители яичницы.
Сколько яиц можно съесть натощак?
Ответ: Только одно. Все следующие уже будут съедены не на пустой желудок.
Задача №5 Влезет или нет?
Это старинная головоломка.
Вырежьте в листе плотной бумаги круглую дырку и предложите кому-нибудь просунуть в нее монетку, бОльшую по диаметру. Надрывать бумагу или каким-то образом сгибать и ломать, а также распиливать монету - нельзя.
Ответ:
Сложите лист бумаги "кульком", дыра должна находиться в самом низу. Затем возьмите бумагу обеими руками и попросите кого-нибудь бросить монетку в "кулек" - пусть она упадет прямо на дно и выглянет нижним концом из дырки. После этого слегка приподнимите углы "кулька" - этого окажется достаточно, чтобы отверстие увеличилось и монетка через секунду-другую вывалилась в дырку. При этом бумага осталась неповрежденной.
Задача №6. Два отца и два сына.
Говорят, что два отца и два сына нашли на дороге, ведущей в Бомбей, три рупии (серебряные монеты) и быстро поделили их между собой, причем каждому досталось по монете. Как им удалось справиться с задачей? Ответ: Путники смогли разделить находку поровну, потому что их было трое: дед, отец и сын (или по-другому - два отца и два сына).
Задача №7 Головоломка в стихах.
Это русская народная потешка, а в ней интересная загадка.
Прилетели галки,
Сели на палки.
Если на каждой палке
Сядет по одной галке,
То для одной галки
Не хватит палки.
Если же на каждой палке
Сядет по две галки,
То одна из палок
Будет без галок.
Сколько было галок?
Сколько было палок?
Ответ:
Четыре галки, три палки.
Задача №8 Как выбрать нужного парикмахера?
Будучи проездом в маленьком городке, один купец зашел перекусить в ресторанчик, а потом решил постричься. В городке было всего две парикмахерские, и в каждой - только один мастер, он же хозяин. В одной парикмахер был неопрятно побрит и плохо пострижен, а в другой - чисто выбрит и с отличной стрижкой. Купец решил стричься в первой парикмахерской. Как по-вашему, он сделал правильный выбор?
Ответ:
Купец верно рассудил, что что раз в городе всего два парикмахера, то они наверняка стригут друг друга. Значит, идти стричься надо к тому, у кого плохая стрижка.
Задача №9 Бочонок кваса.
Один человек выпивает бочонок кваса за 14 дней, а вместе с женой выпивает такой же бочонок кваса за 10 дней. Нужно узнать, за сколько дней жена одна выпивает такой же бочонок кваса . Решение
За 140 дней человек выпьет 10 бочонков кваса, а вдвоём с женой за 140 дней они выпьют 4 бочонков кваса. Значит, за 140 дней жена выпьет 14-10=4 бочонка кваса, а тогда один бочонок она выпьет за 140:4=35 дней.
Задача №10 Как поделить?
Как разделить 5 яблок между пятью лицами так, чтобы каждый получил по яблоку и одно яблоко осталось в корзине.
Ответ: Один человек берет яблоко вместе с корзиной.
Задача №11 Разделить по справедливости.
Трое крестьян: Иван, Петр и Николай - за выполненную работу получили мешок зерна. На беду под рукой не оказалось мерки и пришлось делить зерно на глазок. Старший среди крестьян - Иван - рассыпал зерно на три кучи, как он считал, поровну:
- Первую кучу возьми ты, Петр, вторая достанется Николаю, а третья мне.
- Я не согласен на это, - возразил Николай, - моя куча зерна ведь самая маленькая.
Поспорили крестьяне. Чуть до ссоры не дошло. Пересыпают зерно из одной кучи в другую, из другой в третью и никак к согласию не придут, обязательно кто-нибудь недоволен.
- Будь мы вдвоем, я да Петр, - вскричал в сердцах Иван, я бы мигом разделил. Рассыпал бы зерно на две равные кучи и предложил бы Петру выбрать любую, а оставшуюся взял бы себе. Оба мы были бы довольны. А тут не знаю, как и быть. Задумались крестьяне, как же разделить зерно, чтоб все были довольны, чтоб каждый был уверен, что получил не меньше трети. И придумали. Придумайте и вы.
Ответ:
Иван предложил делить зерно так:
- Я рассыпаю зерно на три кучи, на мой взгляд, поровну и отхожу в сторону. Мне подойдет любая из куч. Пусть затем Петр укажет наименьшую, по его мнению, кучу зерна. Если Николай также посчитает, что зерна в этой куче меньше трети, то отдайте ее мне, а остаток зерна делите между собой известным уже способом. Если же Николай решит, что в указанной куче не меньше трети зерна, пусть возьмет ее себе. Петр возьмет наибольшую, по его мнению, кучу, а оставшаяся достанется мне. Крестьяне последовали предложению Ивана, разделили зерно и, довольные, разошлись.
Задача №12 Задача Диофанта.
Найдите три числа, которые при попарном сложении дают в сумме двадцать, тридцать и сорок.
Ответ: Числа 5, 15 и 25.
Задача №13 Ревнивые мужья. В старинном русском сборнике занимательных задач есть следующая: "Три ревнивых мужа, пришедши с женами своими к берегу реки, нашли при оном лодку, в которую по ее малости более двух человек вмещаться не могло. Почему спрашивается, как бы через реку переехать сим шести человекам так, чтобы ни одна жена с чужим мужем не переезжала и ни на котором берегу не оставалась"
Ответ:
Обозначим пары через Аа, Бб, Вв (маленькими буквами обозначим женщин). Вот схема перевозок, реализующая нужную переправу за 11 рейсов:
| рейс | берег левый | в лодке | берег правый |
|---|---|---|---|
| 1 | Бб Вв | Аа=> | Аа |
| 2 | А Бб Вв | <=А | а |
| 3 | А Б В | б в=> | а б в |
| 4 | Аа Б В | <=а | б в |
| 5 | Аа | Б В=> | Бб Вв |
| 6 | Аа Бб | <=Бб | Вв |
| 7 | а б | А Б=> | А Б Вв |
| 8 | а б в | <=в | А Б В |
| 9 | а | б в=> | А Бб Вв |
| 10 | а б | <=б | А Б Вв |
| 11 | а б=> | Аа Бб Вв |
Стрелки указывают направление движения лодки.
Задача №14 Задача о глубине озера
Задача взята из китайского трактата "Начала искусства вычисления", напечатанного в 1593г. и содержащего ряд статей и задач по арифметике, алгебре и геометрии, причем некоторые вопросы заимствованы из трактата "Арифметика в девяти главах".
ЗАДАЧА: В середине квадратного озера со стороной 10 фунтов растет тросник, выходящий из воды на 1 фут. Если нагнуть тросник, вершина достигнет берега. Как глубоко озеро?
ОТВЕТ: Глубина озера - 12 футов.
Задача №15 Задача из «Арифметики» Л.Ф. Магницкого:
"Некий человек нанял работника на год, обещал ему дать 12 руб. и кафтан. Но тот, отработав 7 месяцев, захотел уйти и просил достойной платы с кафтаном. Хозяин дал ему по достоинству расчет 5 р. и кафтан.
Спрашивается, а какой цены тот кафтан был?"
Алгебраическое решение задачи приводит к уравнению 7 • (x + 12):12 = x + 5, где x руб. — стоимость кафтана.
Арифметическое решение
работник не получил 12 – 5 = 7 (руб.) за 12 – 7 = 5 (месяцев),
поэтому за один месяц ему платили 7:5 = 1,4 (руб.),
а за 7 месяцев он получил 7 •1,4 = 9,8 (руб.),
тогда кафтан стоил 9,8 – 5 = 4,8 (руб.).
Задача №16 Задача из «Всеобщей арифметики» И. Ньютона:
"Мама раздала детям по четыре конфеты, и три конфеты остались лишними. А чтобы дать детям по пять конфет, двух конфет не хватает. Сколько было детей? "
Решение
1) Представим, что мама раздала детям по четыре конфеты. Сколько конфет у нее осталось? — 3. 2) Если она продолжит раздавать конфеты, то по сколько конфет она даст каждому? — По одной (5 – 4 = 1). 3)Скольким детям хватит еще по одной конфете? — Троим. 4) А скольким не хватит? — Двоим. 5) Сколько же было детей? — Пять (3 + 2 = 5).
Задачи из старинных русских рукописей
Задача № 17 На охоте
Пошел охотник на охоту с собакой. Идут они лесом, и вдруг собака увидела зайца. За сколько скачков собака догонит зайца, если расстояние от собаки до зайца равно 40 скачкам собаки и расстояние, которое пробегает собака за 5 скачков, заяц пробегает за 6 скачков? (В задаче подразумевается, что скачки делаются одновременно и зайцем, и собакой.)
Решение.
Если заяц сделает 6 скачков, то и собака сделает 6 скачков, но собака за 5 скачков из 6 пробегает то же расстояние, что и заяц за 6 скачков. Следовательно, за 6 скачков собака приблизится к зайцу на расстояние, равное одному своему скачку. Поскольку в начальный момент расстояние между зайцем и собакой было равно 40 скачкам собаки, то собака догонит зайца через 40ж6 = = 240 скачков.
Задача № 18.
12 человек несут 12 хлебов: каждый мужчина несет по 2 хлеба, женщина - по половине хлеба. А ребенок - по четверти хлеба. Сколько было мужчин, женщин и детей?
Решение:
Как могут распределиться 12 хлебов между мужчинами, женщинами и детьми. Попробуем мысленно распределить хлеба между ними. Сначала дадим всем по половине хлеба. При этом будет роздано 6 хлебов. Чтобы удовлетворить условию задачи, нужно раздать оставшиеся 6 хлебов мужчинам, а затем взять у каждого из детей по четверти хлеба и также распределить этот хлеб среди мужчин. Каждому мужчине до его нормы не хватает полтора хлеба. Шесть хлебов по полтора хлеба можно распределить между четырьмя мужчинами после чего каждый из них будет нести по два хлеба. Отсюда следует, что мужчин не менее пяти. Иначе излишки хлеба, имеющиеся у детей, некому было бы нести. Но если бы мужчин было шесть, то они сами несли бы весь хлеб, а женщинам и детям ничего бы не осталось. Итак, имеется всего пять мужчин. Пятому мужчине до его нормы не хватает полтора хлеба, и именно эти полтора хлеба нужно собрать по четверти. У каждого из детей. Так как полтора хлеба состоят из шести четвертей, то детей имеется всего шестеро и, значит, количество женщин равно 12—5 — 6=1, Следовательно, хлеба несли 5 мужчин, одна женщина и 6 детей.
Ответ:
5 мужчин, одна женщина и 6 детей.
--"Жареные семечки" 20:06, 24 октября 2008 (SAMST)
МОЗГИ ID 215
Фибоначчи создал книгу «Liber abaci», содержащую в себе ряд арифметических и алгебраических заданий.Вот часть из них :
Задача 1-я.
Семь старух отправляются в Рим. У каждой старухи по по семь мулов, каждый мул несет по семь мешков, а в каждом мешке по семь хлебов, в каждом хлебе по семь ножей, каждый нож в в семи ложках. Сколько всего предметов ?
Решение: Задача отличается от Ахмесовой только тем, что к пяти числам лестницы надо прибавить еще шестое число, равное семи т.е 76 = 117649, Всего получится 7 + 72 +73 +74 + 75 + 76 = 137 256 предметов .
Задача 2-я. Таинственная веревка.
Моя темница находилась не ниже рва, а наоборот, в одной из самых верхних частей замка. Дверь была настолько массивной, а замок настолько надежным, что не оставляли надежд убежать этим путем. После многодневных тяжких усилий мне удалось выломать один и зпрутьев решетки в узком окне. Я мог пролезть в образовавшееся отверстие, но расстояние до земли было таково, что вздумав спрыгнуть, я разбился бы насмерть. Тут, к моей великой удаче, в углу темницы я обнаружил забытую кем-то веревку. Однако она оказалась слишком короткой, чтобы безопасно спрыгнуть с его конца. Тогда, я вспомнил, как мудрец из Ирландии удлинял слишком короткое для него одеяло, отрезав ярд снизу и пришив его сверху. Поэтому я поспешил разделить веревку пополам и снова связать две образовавшиеся части. Она стала тогда достаточно длинной, и я смог спуститься вниз живым и невредимым. Как это удалось сделать?
Решение: Шут «разделил веревку пополам»- это вовсе не значит, что он разрезал ее на две равные части. Без сомнения, он просто расплел жгуты, из которых она была свита, и разъединил их, так что у него получились веревки, равные по длине исходной, но вдвое тоньше. Связав их, он получил веревку, в два раза длиннее первоначальной.
Задача 3-я. Через ров.
Теперь я оказался перед широким опоясывающим замок рвом, который был очень глубок. Увы! Я не умел плавать, и мои шансы на спасение были ничтожными, пока я не обнаружил привязанной к стене лодки. Но, забравшись в лодку, я увидел, что в ней нет ни весело, ни любого другого орудия, которым можно было бы грести. Все же я отвязал веревку и оттолкнул лодку от кормы. Но вскоре она остановилась - не было никакого течения. Как же мне удалось переправиться через ров?
Решение: Без сомнения, читатель улыбнется, услышав, что лодка с человеком может двигаться вперед в стоячей воде с помощью причальной веревки. И тем не менее это факт. Если шут привяжет конец веревки к корме,а потом стоя на носу, начнет делать ее резкие рывки, то лодка будет двигаться вперед. Этим часто пользуются на практике и утвердают, что таким образом можно развить скорость от двух до трех миль в час.
Задача 4-я.
Существует народная задача о нищих(или старцах), о которой И.А.Изиосков в своем докладе « О памятниках народной математики», прочитанном в 1884 году в казанском обществе испытателей. «История элементарной математики» трактует эту задачу так, как она распространена среди населения Орловской губ.:
Шли семь старцев. У каждого старца по семь костылей, На каждом костыле по семь сучков, На каждом сучке по семь кошелей, В каждом кошеле по семь пирогов, А в каждом пироге по семь воробьев.
Решение: Задача требует определения чисел всех предметов. Рещение очевидно : 7 + 72 + 73 + 74 + 75 + 76 .
--МОЗГИ ID 215 21:59, 24 октября 2008 (SAMST)
Уважаемые участники! Страница заполнена, продолжение на странице Копилка знаменитых задач продолжение 3.
--ОМЕГА ID 276 10:30, 10 ноября 2008 (SAMST) Задача №1 Получить 7, записав ее пятью двойками. Ответ: 7=2+2:2+22 Задача №2 Получить 28, записав это число пятью двойками. Ответ: 28=2+2+2+22 Задача №3 Записать 23 четырьма двойками. Ответ: 23=22+2:2 Задача №4 Записать 100 четырьма девятками Ответ: 999/9 Задача №5 Записать 100 шестью девятками Ответ: 99 + 99/99 Задача №6 Записать 100 пятью единицами Ответ: 111 - 11 Задача №7 Записать 100 пятью тройками Ответ: 3 х 33 + 3 : 3 Задача №8 Записать 100 пятью пятерками Ответ: (5 х 5 х 5) - (5 х 5) Задача №9 Число 100 изобразить пятью одинаковыми цифрами Ответ: 111 - 11; 3 х 33 + 3 : 3; (5 х 5 х 5) - (5 х 5) Задача №10 Записать 100 при помощи шести девяток Ответ: 9999/99 Задача "11 Записать 100, пользуясь пять раз цифрой Ответ: 33 х 3 + 3 : 3 = 100