Семинар ДООМ. Решение задач на применение теории графов.
участник: Болонина Людмила Александровна, 022.
Урок №1.
Тема: Цепи. Головоломки.
Цели:
познакомиться со свойствами графов;
разобрать закономерности проведения эйлеровых линий без повторений и без отрыва карандаша от бумаги;
показать решение головоломок на языке теории графов, привить интерес к математике.
Ход урока:
Рассмотрим следующую головоломку:
Вы, наверное, знаете, что есть такой город Калининград, раньше он назывался Кенигсберг. Через город протекает речка Преголя.
Она делится на два рукава и огибает остров. В XVIII веке в городе было семь мостов, расположенных так, как показано.
Рассказывают, что однажды житель города спросил у своего знакомого, сможет ли он пройти по всем мостам так, чтобы на каждом
из них побывать только один раз и вернуться к тому месту, откуда началась прогулка. Многие горожане заинтересовались этой
задачей, однако придумать решение никто не смог. Этот вопрос привлек внимание ученых разных стран. Разрешить проблему
удалось известному математику Леонарду Эйлеру. Причем, он не только решил эту конкретную зада¬чу, но придумал общий метод
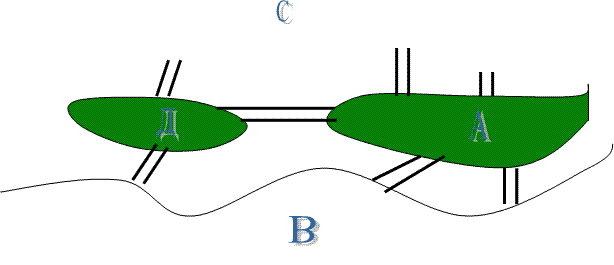
решения подобных задач. Эйлер посту¬пил следующим образом: он «сжал» сушу в точки, а мосты «вытянул» в ли¬нии.
В результате получилась фигура, изображенная на рис.
Такую фигуру, состоящую из точек и линий, связывающих эти точки, называют графом. Точки А, В, С, D называют вершинами графа, а линии, которые соединяют вершины - ребрами графа. На рис. 2 из вершин B, С, D выходят по 3 ребра, а из вершины А -5 ребер. Вершины, из которых выходит нечетное число ребер, называют нечетными вершинами, а вершины, из которых выхо¬дит четное количество ребер, - четными.
Решая задачу про кенигсбергские мосты, Эйлер установил, в частности,
свойства графа:
• Если все вершины графа четные, то можно одним росчерком
(т.е. не отрывая карандаша от бумаги и не проводя дважды по одной и той же линии)
начертить граф. При этом движение можно начать с любой вершины и окончить в той же вершине.
• Граф с двумя нечетными вершинами тоже можно начертить одним росчерком.
Движение надо начинать от любой нечет¬ной вершины, а заканчивать на другой нечетной вершине.
• Граф с более чем двумя нечетными вершинами невозможно начертить одним росчерком.
В задаче о семи кенигсбергских мостах все четыре вершины соответствующего графа нечетные, т.е. нельзя пройти по всем мостам один раз и закончить.путь там, где он был начат. Широко известны в популярной литературе задачи, в которых предлагается выйти из лабиринтов. Эти задачи можно решить, используя правило Тарри: построение цепи, проходящей вдоль всех ребер графа в точности по одному разу в каждом направлении. Рассмотрим задачу на проведение эйлеровских линий без повторений и без отрыва карандаша от бумаги.
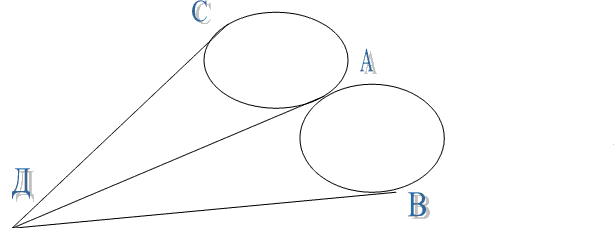
ЗАДАЧА:
Начертить фигуру одной линией, не отрывая карандаша от бумаги и не проводя дважды линий карандашом.
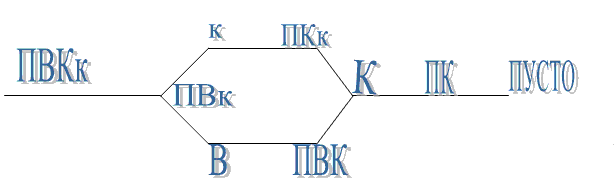
При решении подобных задач необходимо помнить следующее положение. Для того, чтобы на графе имелась цепь, соединяющая А и В, содержащая все его ребра в точности по одному разу, необходимо и достаточно, чтобы А и В были единственными нечетными вершинами. (В нашем примере это вершины В и А). Многие известные головоломки могут быть изложены на языке теории графов. Так, решение широкоизвестной задачи о перевозке козы (К), волка (В) и капусты (к) можно представить в виде графа, изображенного на рисунке. Перевозчик обозначен буквой (П).
Из графа видно, что решение может быть получено двумя способами.
Домашнее задание:
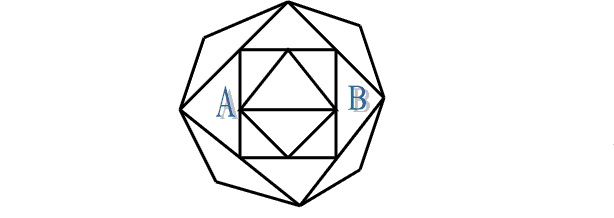
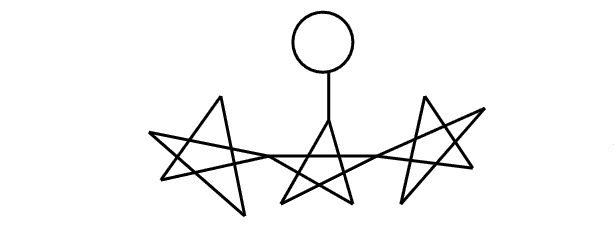
Задача: Можно ли с одного росчерка вычертить такую фигуру?
Урок составила Болонина Л.А. команды 022, г. Казани. Этот урок проводился в 7 классе.