Семинар ДООМ. Урок-семинар по теме: Пифагорейская школа и теорема Пифагора.

Семинар ДООМ. Урок-семинар по теме: Пифагорейская школа и теорема Пифагора.
8 класс
Участник: Коннова Елена

Руководитель команд ДООМ 2009 Многоугольник IDm 083 и Великие математики IDm 082

Презентация к статье Пифагорейская школа и теорема Пифагора

Вид семинара:

Обсуждение поставленных вопросов с использованием в ходе предварительной подготовки разнообразных источников.

Предварительная подготовка.

1. Подготовка двух докладов:
- о пифагорейском союзе,
- о геометрических достижениях пифагорейской школы.
2. подготовка доказательства теоремы Пифагора по учебнику.
План урока.
Класс разбит на 4-5 групп. Орг. вопросы (2 мин.)
Вступление учителя(3 мин.)
Доклады учеников (10 мин.)
История пифагорейского союза

Основателем союза был Пифагор. Его расцвет приходится на время правления тирана Поликрата (ок. 530 г.). Пифагор основал сообщество в италийском городе Кротоне. Умер он в Метапонте, куда переселился вследствие враждебного отношения кротонцев к его союзу.

После смерти Пифагора вражда против пифагорейского союза усиливалась во всех демократиях Великой Греции и в середине V в. разразилась катастрофой: в Кротоне многие пифагорейцы были убиты и сожжены в доме, где они собрались; разгром повторился и в других местах. Уцелевшие были вынуждены бежать, разнося с собой учение и мистерии своего союза.

Пифагорейцы были известны в античности также своим вегетарианством, связанным с учением о переселении душ.

Согласно традиции, последователи Пифагора делились на акусматиков («слушателей») и математиков («учеников»). Акусматики имели дело с религиозными и ритуальными сторонами учения, математики — с исследованиями четырёх пифагорейских «матем»: арифметики, геометрии, гармоники и сферики.

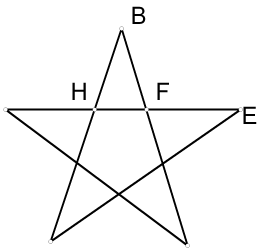
Излюбленной фигурой пифагорейцев была пятиконечная звезда. Она символ четырёх пифагорейских «матем».

Все законы и устройство мира по Пифагору подчиняются четким математическим законам гармонии, заложенным в звучании небесных сфер - луны, солнца, пяти планет и звезд. Расстояние между сферами и издаваемые ими звуки соответствуют гармоническим музыкальным интервалам. И в наши дни эта теория гармонии космоса имеет своих приверженцев.

Открытия Пифагора, основанные на применении математических методов, сыграли большую роль в развитии астрономии и географии. В частности, он одним из первых утверждал, что Земля имеет шарообразную форму. Учился же Пифагор математике в Египте и Вавилоне. Считается, что он первым применил в геометрии метод логического доказательства.

Пифагорейская геометрия Из геометрических работ пифагорейцев на первом месте стоит знаменитая теорема Пифагора. Содержание пифагоровой теоремы было впервые обнаружено рациональными прямоугольными треугольниками с катетом, выражаемым нечётным числом.

Вопрос о подобном свойстве также и других прямоугольных треугольников требовал соизмерения их сторон. При этом пифагорейцам впервые пришлось встретиться с несоизмеримыми линиями. (В алгебре это вопрос о иррациональных числах). Первоначальное доказательство основывалось на сравнении площадей.

Пифагорейцы также дали общее доказательство теоремы о равенстве внутренних углов треугольников двум прямым; они были знакомы со свойствами и построением правильных 3-, 4-, 5- и 6-угольников.

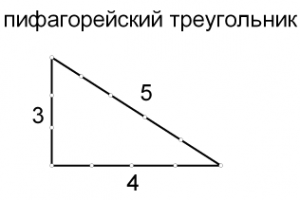
В стереометрии предметом занятий пифагорейцев были правильные многогранники. Собственные исследования пифагорейцев прибавили к ним додекаэдр. Так называемые "пифагорейские" треугольники были известны еще в Древнем Египте. Пифагорейскими называются такие подобные треугольники, стороны которых соотносятся как 3:4:5, все они являются прямоугольными.

Египтянам знание этого соотношения помогало при вычислении площадей прямоугольных земельных наделов. Пифагору же приписывают установление более общего соотношения сторон прямоугольного треугольника, знаменитая теорема Пифагора. Впрочем, в Китае эта теорема была известна еще за 500 лет до Пифагора!

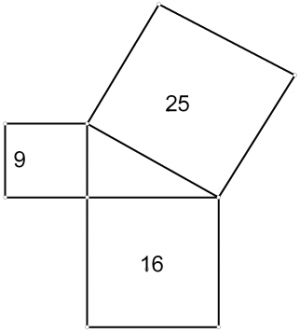
Практическая работа (5 мин.)
Давайте попробуем построить на сторонах треугольника 3,4,5 квадраты. Теперь посчитаем площадь этих квадратов. Их площадь 9,16 и 25. Видим, что выполняется соотношение 9+16=25. Оказывается, для всех прямоугольных треугольников верно, что сумма квадратов катетов равна квадрату гипотенузы.

Давайте докажем эту теорему.
Ученик доказывает теорему Пифагора у доски по рисунку из учебника. (5 мин.)

После этого 3 группы получают задание – найти другие доказательства теоремы Пифагора по другим рисункам, две группы – выразить катеты через другой катет и гипотенузу и решить простые задачи на прямое применение теоремы. (5 минут)

Задания для групп
Задание 1.
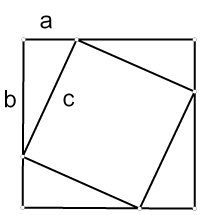
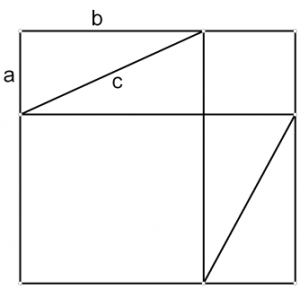
Доказать теорему Пифагора, используя рисунок:

Рис. А)

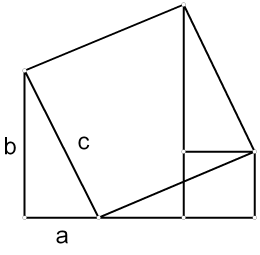
рис. В)

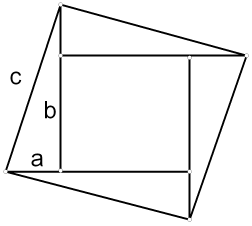
рис.С)
Задание 2.
Дан прямоугольный треугольник с гипотенузой c и катетами a и b.Выразите a,если известно b и с.
Найдите катет, если а) гипотенуза равна 100 см, а второй катет 80 см.
а) гипотенуза равна 13 см, а второй катет 5 см.
Задание 3.
Попробуйте найти катеты пифагорова треугольника, если его гипотенуза равна 17, 25, 29, 41.

Обсуждение доказательств, решение задач - 20 минут.
Если класс быстро справится с решением задач, можно предложить задачи из учебника № 485, 487, 488, 490.
Подведение итогов урока, обобщение, домашнее задание – 5 минут..