Семинар ДООМ. Факультативное занятие. Конкурсные задачи на проценты.
Участник:Москевич Лариса Вячеславовна, ID-224
Цель.
1. Познакомить учащихся с задачами, предлагавшимися на вступительных экзаменах в ВУЗ.
2. Рассмотреть способы решения таких задач.
Задача №1(МГУ, физфак)
Руда содержит 40% примесей, а выплавленный из нее металл содержит 4 % примесей. Сколько получится металла из 24 тонн руды?
Решение.
| № | Количество (т) | Количество чистого металла (т) | Процент % |
|---|---|---|---|
| руда | 24 | 0,6*24 = 0,96х | 60% |
| металл | x | 0,96х | 96% |
0,6*24 = 0,96х
Х=15
Ответ 15 тонн.
Задача №2(МГУ, экономический факультет)
Имеются два бака: первый бак наполнен чистым глицерином, второй бак – водой. Взяли два двухлитровых ковша, зачерпнули полным первым ковшом глицерин из первого бака, полным вторым ковшом – воду из второго бака, после чего первый ковш влили во второй бак, а второй ковш – в первый бак. Затем перемешали, снова зачерпнули полным первым ковшом смесь из первого бака, полным вторым ковшом смесь из второго бака, и влили первый ковш во второй бак, а второй – в первый бак. В результате 40% объема первого бака занял чистый глицерин. Определить суммарный объем баков, если известно, что второй бак в четыре раза больше по объему первого бака.
Решение.
| № | Количество V (л) | Количество V глицерина первоначально(л) | Процент % глицерина |
|---|---|---|---|
| 1 бак | x | x | 100% |
| 2 бак | 4x | 0 | 0% |
| № | Количество V (л) | Количество V глицерина после 1-го переливания(л) | Процент % глицерина |
| 1 бак | x | x-2 | (х-2)*100%/х |
| 2 бак | 4x | 2 | 2*100%/4х |
| № | Количество V (л) | Количество V глицерина после 2-го переливания(л) | Процент % глицерина |
| 1 бак | x | Х-2 -(х-2)*2 /х + 2*2/4х = 0,4х | 40% |
х-2 -(х-2)*2 /х + 2*2/4х = 0,4х,
(х-2)^2 – 0,4x^2 = 0,
решая уравнение и анализируя решения делаем вывод, что
х =5, 4х+х = 20+5 = 25.
Ответ. 25литров.
Задача №3(МГУ, экономический факультет)
Команда школьников, состоящая из мальчиков и девочек, участвовала в командных соревнованиях по шахматам. Мальчики этой команды сыграли в совокупности 60 партий, а девочки- 40. Из всех сыгранных мальчиками партий, мальчики выиграли 45% партий, а из всех сыгранных девочками партий, девочки проиграли 50% партий. Мальчики проиграли на 7 партий больше, чем девочки сыграли вничью. За победу в одной партии дается одно очко, за ничью – 0,5 очка, за поражение 0 очков. Школьники одной и той же команды друг с другом не играют. Определить, сколько очков завоевано мальчиками этой команды, если вся команда набрала 52 очка.
Решение.
Мальчики выиграли 60*0,45 = 27 партий. Девочки выиграли или сыграли вничью 40*0,5 =20 партий. Пусть мальчики вничью сыграли х партий, тогда они проиграли (60-27)-х = 33-х партий, что на 7 партий больше, чем девочки сыграли вничью.
Значит, вничью девочки сыграли 33-х-7 = 26 – х партий.
Всего девочки и мальчики набрали 52 очка.
Составим и решим уравнение:
27*1+х*0,5+(20-(26-х))*1 + (26-х)*0,5 = 52,
х = 18.
Очки, завоеванные мальчиками:
27*1+18*0,5 = 36.
Ответ. 36 очков.
Задача №4(ГУ ВШЭ)
В течение трех лет вкладчик имел одинаковый процент прибыли по отношению к каждому предыдущему году, а затем, в течение двух лет нес убытки ежегодно в половине процентов по сравнению с процентами прибыли. При какой исходной процентной ставке, не превышающей 200% годовых, вкладчик будет иметь наибольшую итоговую прибыль за пять лет и какова она по отношению к первоначальному вкладу?
Решение.
Пусть А0 – начальный капитал, х – доля прибыли, соответствующая х*100% проценту прибыли по отношению к каждому предыдущему году в течение 3-х лет, тогда х/2-соответствующая доля убытков в каждые два последующих года.
Величина вклада за пять лет:
А = А0(1+х)^3(1-[/2)^2.
Необходимо найти А(х), если 0≤х≤2 (до 200%)
Производная А’(x) = A0(1+x)^2(1-x/2)(2-2,5x).
Критические точки, принадлежащие [0;2]: х = 2 и х = 4/5.
A(4/5) наибольшее = А0(1+4/5)^3(1-2/5)^2 = A0* 3436/1125 > A0,
искомый процент равен 4/5*100% = 80%
Относительная прибыль (А-А0)/А0 = 311/1125
Абсолютная прибыль А-А0 = 311/1125 А0.
Ответ. 80%, 311/1125 А0.
Задача №5(ГУ ВШЭ)
Фирма при продаже катеров двух типов А и В имеет соответственно прибыль: по типу А – 2000$, по типу В – 1000$ (в долларах) за каждый катер. Спрос на катера диктует следующие ограничения: общее число катеров, проданных фирмой за неделю не менее 12 штук, но меньше 15 штук. Число катеров типа В при этом составляет не более 25 % от общего числа проданных за неделю, причем не менее 2 штук. Вычислить максимальную прибыль фирмы за неделю и число проданных катеров каждого типа.
Решение.
Пусть х и у – число проданных катеров типов А и В по цене 2000 и 1000 долларов соответственно.
Прибыль, полученная от продажи:
S = 2000x+1000y.
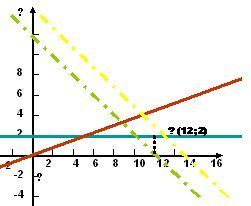
По условию задачи 12 ≤х +у≤15, 2≤у≤0,25(х+у).
у≥2, y≤х/3, 12-х≤у≤15-х.
Построим.
Из геометрических соображений точка (12;2) является искомой, для которой прибыль будет наибольшей
S = 12*2000+2*1000 = 26000$.
Ответ.
Максимальная прибыль 26000$, катеров типа А – 12 штук, типа В – 2.
Задача №6 (ЗФМШ при МФТИ)
В корзине лежало не более 70 грибов. После разбора оказалось, что 52% из них - белые. Если отложить три самых маленьких гриба, то среди оставшихся будет ровно половина белых. Сколько грибов было в корзине?
Решение.
Пусть в корзине лежало x белых и у небелых грибов.
Белых – 52%, т.е. х = 0,52(х+у).
0,48х = 0,52у, у =12х/13.
Из корзины взяли 3 гриба, пусть из них а белых, 0≤а≤3.
После чего белых и небелых в корзине осталось равное количество.
х - а = 0,5(х+у-3), у = 12х/13.
Решая, получаем х = 26а – 39.
Т.к. а – целое и 0≤а≤3, и х и у –натуральные,
то а=2, х = 13, у = 12.
х+у = 25.
Ответ. 25 грибов было в корзине.
--Москевич Лариса Вячеславовна 20:12, 8 ноября 2008 (UZT)