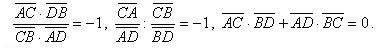Семинар ДООМ: Урок-лекция "Гармонические четверки точек. Их свойства"

Автор: Шувалова Ю.Г.

Тема урока: Гармонические четверки точек. Их свойства.

Класс: 8-9 (углубленное изучение)

Тип урока: урок-лекция изучения нового материала.

МАТЕРИАЛ К УРОКУ

Введем обозначения: AB, CD (со стрелкой) – ненулевые коллинеарные векторы; AB, CD (с чертой)– их длины, взятые с одинаковыми знаками, если векторы сонаправлены, и с разными знаками, если они противоположно направлены. Тогда, в частности, выражения и будут представлять отношение и произведение, взятые со знаком «+», если векторы сонаправлены, и со знаком «–»,они противоположно направлены.

Воспользуемся принятыми обозначениями для определения гармонических четверок точек. Рассмотрим четыре точки А, В, С, D, лежащие на одной прямой. Будем говорить, что точки А, В, С, D (взятые в том же порядке, как указано) образуют гармоническую четверку, если

(*)

Из равенства следует, что среди данных векторов три вектора сонаправлены, а четвертый вектор направлен противоположно по отношению к ним.

Отметим, что данное равенство равносильно каждому из следующих равенств:

Можно написать еще несколько равенств, равносильных (*).

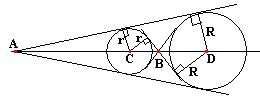
Задача: К двум окружностям разных радиусов, расположенным вне друг друга, проведены две внешние и две внутренние общие касательные. Внешние касательные пересекаются в точке А, внутренние – в точке В, точки С и D – центры окружностей. Доказать, что точки А, В, С, D образуют гармоническую четверку.

Решение: Точки А, В, С, D лежат на одной прямой. Радиусы окружностей обозначим r, R. Тогда, используя подобие прямоугольных треугольников, получаем длины векторов АС:АD=r:R и длины векторов DВ:СВ=-r:R. Отсюда следует, что 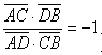. Это равенство равносильно равенству (*), а это означает, что точки А, В, С, D образуют гармоническую четверку.

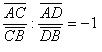
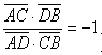
Замечание: Гармонические четверки обладают определенной симметрией: если А, В, С, D – гармоническая четверка, то C, D, A, B также гармоническая четверка. Это следует из того, что равенство равносильно равенству . При этом говорят, что точки А и В гармонически разделяют точки С и D, а точки С и D гармонически разделяют точки А и В.

Свойства гармонических четверок:

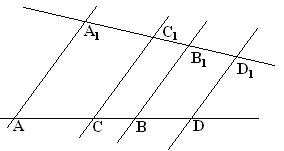
1. Через точки А, В, С, D, лежащие на одной прямой, проведем 4 параллельные прямые. Пусть А1, В1, С1, D1 – точки пересечения этих прямых с какой-нибудь другой прямой. Тогда, если А, В, С, D – гармоническая четверка, то А1, В1, С1, D1 также гармоническая четверка.

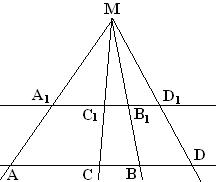
2. Аналогичным свойством обладают точки А1, В1, С1, D1 пересечения прямых МА, МВ, МС, MD с какой-нибудь прямой, параллельной прямой АD.

Рассмотрим задачу, связанную с гармоническими четверками.

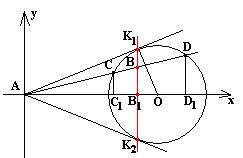
Задача: Из данной точки А проведены к данной окружности с центром О касательные АК1, АК2 и секущая, пересекающая окружность в точках С и D, а отрезок К1К2 в точке В. доказать, что точки А, В, С, D образуют гармоническую четверку.

Решение: Введем систему координат с началом в точке А (как показано на рисунке) Пусть точки В1, С1, D1 проекции точек В, С, D на ось абсцисс. Докажем, что точки А, В1, С1, D1 образуют гармоническую четверку. Отсюда сразу же последует, что точки А, В, С, D образуют гармоническую четверку.

Уравнение окружности имеет вид: , где а=АО, R – радиус окружности. Уравнение секущей АD: y=kx, где k – некоторое число. Координаты точек С, D удовлетворяют данным уравнениям.

Если подставить y=kx в у равнение окружности, то получим квадратное уравнение , корни которого х1 и х2 равны абсциссам точек С, D, т.е. АС1=х1, AD1=х2. По теореме Виета:

Прямая К1К2 называется полярой данной точки А относительно данной окружности.

Нетрудно доказать, что если точка В не лежит на поляре, а прямая АВ пересекает окружность в точках С и D, то точки С, D уже не будут гармонически разделять точки А и В. Поэтому можно сделать вывод: если данная точка А лежит вне данной окружности, то множество точек В, для каждой из которых точки пересечения прямой АВ и окружности гармонически разделяют точки А и В, представляет собой часть поляры точки А относительно данной окружности, лежащую внутри этой окружности.

Рассмотрим еще одну задачу: построение касательной с помощью одной линейки.

Как с помощью циркуля и линейки построить касательную к окружности через данную точку?

Оказывается, построение такой касательной можно выполнить, не используя циркуля, т.е. с помощью одной линейки.

Сначала рассмотрим определение четырехвершинника и задачу.

Возьмем 4 точки, три из которых не лежат на одной прямой, и соединим их попарно отрезками. Полученная фигура, состоящая из шести отрезков, называется четырехвершинником. Четырехвершинник имеет вид четырехугольника, в котором провели диагонали.

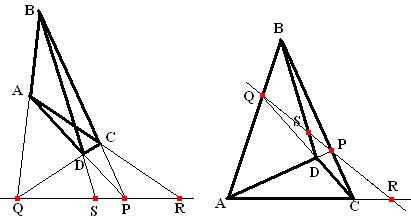
Задача: В четырехвершиннике АВСD непересекающиеся отрезки АD и ВС, а также АВ и СD продолжены до пересечения в точках Р и Q соответственно. Прямая РQ пересекает прямую АС в точке R, а прямую ВD в точке S. Доказать, что точки P и Q гармонически разделяют точки R и S.

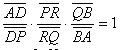
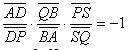
Решение: Рассмотрим APQ. На его сторонах (либо их продолжениях) взяты точки R, B, В так, что прямые AR, PB, QD пересекаются в одной точке С. Отсюда по теореме Чевы следует, что . С другой стороны, на сторонах этого же треугольника (либо их продолжениях) взяты точки D, B, S, лежащие на одной прямой. Следовательно, по теореме Менелая . Разделив первое равенство на второе, получим: . Это означает, что точки P, Q, R, S образуют гармоническую четверку.

Вернемся к вопросу построения касательной к окружности одним циркулем.

Дана окружность и точка М вне этой окружности. Провести через точку М касательную к данной окружности с помощью только линейки.

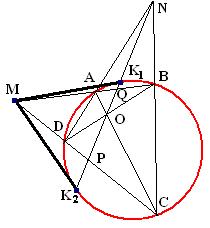
Решение: Проведем через М какие-нибудь две секущие, пересекающие данную окружность в точках А и В, С и D соответственно. Затем проведем диагонали АС и ВD четырехугольника АВСD и обозначим буквой О точку их пересечения. Стороны АD и ВС продолжим до пересечения в точке N. Проведем прямую ON и обозначим через К1, К2 точки пересечения с окружностью. Осталось провести прямые МК1 и МК2 - это и есть искомые касательные.

Доказательство: Обозначим буквами Q и Р точки пересечения прямой К1К2 с отрезками АВ и СD и рассмотрим четырехвершинник АОВN. Согласно задаче точки В и С гармонически разделяют точки М и Р. Значит, точка Р лежит на поляре точки М относительно данной окружности. Аналогично: четырехвершинник СОDN. Точки В и А гармонически разделяют точки М и Q. Значит, точка Q лежит на поляре точки М относительно данной окружности. Таким образом, прямая PQ (что тоже К1К2) есть поляра точки М относительно данной окружности. Значит, МК1 и МК2 - это и есть искомые касательные.

Домашнее задание:

1. Напишите равенства, равносильные равенству .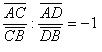

2. Докажите свойства гармонических четверок.

3. Задача: В треугольнике АВС отрезок АА1 – высота, отрезок АА2 – биссектриса, А1 не совпадает с А2, точки К1 и К2 – точки касания вписанной и вневписанной окружностей со стороной ВС. Доказать, что точки А1, А2, К1 и К2 образуют гармоническую четверку.

Список литературы.

• Геометрия: Доп. Главы к шк. учеб. 9 кл.: Учеб. пособие для учащихся шк. и кл. с углубленным изуч. математики/ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, И.И. Юдина. – М.: Просвещение, 1997.
• Шарыгин И.Ф.Факультативный курс по математике: Решение задач: Учеб. пособие для 10 кл. сред. шк. – М.: Просвещение, 1989.