Семинар ДООМ: Урок-лекция "ИНВЕРСИЯ"

Автор: Шувалова Ю.Г.

Тема урока: Инверсия. Основные свойства инверсии.

Класс: 8-9 (углубленное изучение)

Тип урока: урок-лекция изучения нового материала.

МАТЕРИАЛ К УРОКУ:

Сегодня мы рассмотрим одно геометрическое преобразование, называемое инверсией. Начнем с определения.

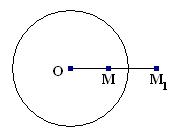
Инверсией относительно окружности с центром в точке О радиуса К называется отображение плоскости (без точки О) на себя, при котором каждой точка М, отличной от О, сопоставляется такая точка М1 луча ОМ, что ОМ1*ОМ=R*R; точке О не сопоставляется никакая точка. Точка О называется центром инверсии, а величина R – ее радиусом.

Непосредственно из определения инверсии видно, что точки окружности S она оставляет на месте, точки, лежащие внутри S, переводит наружу, а точки, лежащие вне S, - внутрь S. Если точка A переходит при инверсии в A*, то точку A* эта инверсия переводит в A, т. е. (A*)* = A. Образом прямой, проходящей через центр инверсии, является сама эта прямая.

В этом месте надо сделать оговорку, связанную с тем, что инверсия не является в строгом смысле слова преобразованием плоскости, так как точка O никуда не переходит. Поэтому формально мы не имеем права говорить об «образе прямой, проходящей через точку O», а должны рассматривать объединение двух лучей, получающихся из прямой выбрасыванием точки O. Аналогично обстоит дело и с окружностями, содержащими точку O. Мы, тем не менее, будем придерживаться этих нестрогих, но зато более наглядных формулировок, надеясь, что читатель легко восстановит точный смысл.

Всюду образ точки A при инверсии обозначается через A*. Сформулируем важнейшие свойства инверсии, постоянно использующиеся при решении задач.

При инверсии с центром O:

Задача 1: Пусть при инверсии с центром O точка A переходит в A*, а точка B - в B*. Докажите, что треугольники OAB и OB*A* подобны.

Решение: Пусть R в квадрате - степень инверсии. Тогда OA *OA* = OB * OB* = R*R, откуда OA : OB = OB* : OA* и треугольники OAB и OB*A* подобны, поскольку углы AOB = B*OA*.

Свойство 1: прямая l, не содержащая O, переходит в окружность, проходящую через O (задача 2);

Задача 2: Докажите, что при инверсии с центром O прямая l, не проходящая через O, переходит в окружность, проходящую через O.

Решение: Опустим из точки O перпендикуляр OC на прямую l и возьмем произвольную точку M на l. Из подобия треугольников OCM и OM*C* (задача 1) следует, что углы OM*C* = OCM = 90 градусов, т. е. точка M* лежит на окружности S с диаметром OC*. Если X - какая-то точка S, отличная от O, то она является образом при инверсии точки Y пересечения прямых l и OX (так как образ точки Y лежит, с одной стороны, на луче OX, а с другой стороны, как уже доказано, на окружности S). Итак, инверсия переводит прямую l в окружность S (без точки O).

Свойство 2: окружность с центром C, проходящая через O, переходит в прямую, перпендикулярную OC (задача 3);

Задача 3: Докажите, что при инверсии с центром O окружность, проходящая через O, переходит в прямую, а окружность, не проходящая через O, - в окружность.

Решение: Случай, когда окружность S проходит через O, фактически был разобран в предыдущей задаче (и формально следует из нее, так как (M*)* = M). Предположим теперь, что точка O не принадлежит S. Пусть A и B - точки пересечения окружности S с прямой, проходящей через O и центр S, а M - произвольная точка S. Докажем, что образом S является окружность с диаметром A*B*. Для этого достаточно показать, что угол A*M*B* = 90 градусов. Но согласно задаче 1 треугольники OAM, OM*A* подобны и треугольники OBM, OM*B* подобны, следовательно, углы OMA = OA*M* и углы OMB = OB*M*, точнее, угол (OM, MA) = – угол (OA*, M*A*) и угол (OM, MB) = – угол (OB*, M*B*) (чтобы не рассматривать различные случаи расположения точек, мы воспользуемся свойствами ориентированных углов между прямыми). Поэтому угол (A*M*, M*B*) = угол (A*M*, OA*) + угол (OB*, M*B*) = угол (OM, MA) + угол (MB, OM) = угол (MB, MA) = 90 градусов.

Свойство 3: окружность, не проходящая через O, переходит в окружность, не проходящую через O) (задача 3);

Свойство 4: касание окружностей и прямых сохраняется, если только точка касания не совпадает с центром инверсии; в последнем случае получается пара параллельных прямых (задача 4);

Задача 4: Докажите, что касающиеся окружности (окружность и прямая) переходят при инверсии в касающиеся окружности или в окружность и прямую, или в пару параллельных прямых.

Определение. Пусть две окружности пересекаются в точке A. Углом между окружностями называют угол между касательными к окружностям в точке A. (Ясно, что если окружности пересекаются в точках A и B, то угол между касательными в точке A равен углу между касательными в точке B.) Аналогично определяется угол между прямой и окружностью.

Решение: Если точка касания не совпадает с центром инверсии, то после инверсии эти окружности (окружность и прямая) будут по-прежнему иметь одну общую точку, т. е. касание сохранится.

Если окружности с центрами A и B касаются в точке O, то при инверсии с центром O они перейдут в пару прямых, перпендикулярных AB. Наконец, если прямая l касается в точке O окружности с центром A, то при инверсии с центром O прямая l переходит в себя, а окружность - в прямую, перпендикулярную OA. В каждом из этих случаев получаем пару параллельных прямых.

Свойство 5: величина угла между двумя окружностями (или между окружностью и прямой, или между двумя прямыми) сохраняется (задача 5).

Задача 5: Докажите, что при инверсии сохраняется угол между окружностями (между окружностью и прямой, между прямыми).

Решение: Проведем через точку пересечения окружностей касательные l1 и l2. Так как при инверсии касающиеся окружности и прямые переходят в касающиеся (по задаче 4), то угол между образами окружностей равен углу между образами касательных к ним. При инверсии с центром O прямая li переходит в себя или в окружность, касательная к которой в точке O параллельна li. Поэтому угол между образами прямых l1 и l2 при инверсии с центром O равен углу между этими прямыми.

Список литературы.

• Геометрия: Доп. Главы к шк. учеб. 9 кл.: Учеб. пособие для учащихся шк. и кл. с углубленным изуч. математики/ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, И.И. Юдина. – М.: Просвещение, 1997.
• Шарыгин И.Ф.Факультативный курс по математике: Решение задач: Учеб. пособие для 10 кл. сред. шк. – М.: Просвещение, 1989.