Семинар ДООМ "Задачи по теме "Можно ли не ломая проволоки изготовить каркас куба?"
Задача 1
Покажите, что если бы в задаче Эйлера число мостов оказалось на один больше или на один меньше, то по ним можно было бы пройти, побывав на каждом один раз. Нарисуй соответствующий граф.
Задача 2
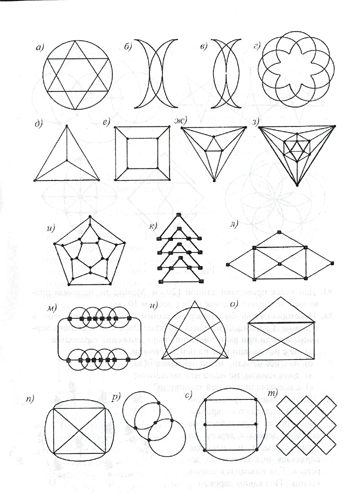
Если возможно, изобразите одним росчерком графы, представленные на рисунке. Указание: если на рисунке вершины графа не выделены, то ими следует считать точки самопересечения.
Задача 3
Какие буквы русского алфавита уникурсальны?
Задача 4
Некоторый граф был начерчен одним росчерком, при этом в вершине А карандаш побывал трижды. Определите степень вершины А, если при вычерчивании графа движение карандаша:
а) не с нее начали и не на ней закончили;
б) не с нее начали, но на ней закончили;
в) с нее начали, но не на ней закончили;
г) с нее начали и на ней закончили.
Задача 5
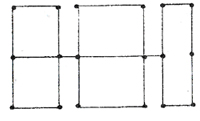
Где на выставке следовало бы сделать вход и выход (рис. 2), чтобы мож-но было провести экскурсию по всем залам, побывав в каждом из них в точности один раз?
Задача 6
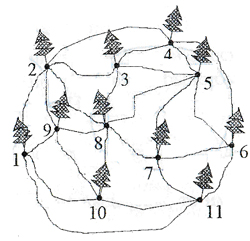
В небольшой роще находится кролик (рис. 3). Выскочив из норы и бегая по снегу от дерева к дереву, он оставил следы и, наконец, спрятался под одним из деревьев. Где сейчас находится кролик? Под каким деревом находится его нора? Сколько решений имеет задача?
Задача 7
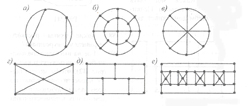
Определить наименьшее число росчерков, которыми можно начертить каждую из фигур на рисунке 4.