Семинар ДООМ "Круги Эйлера"

Круги Эйлера

Участник:Маклецова И.А. учитель математики Маклецова Ирина Анатольевна, ID_236

Тема: «Круги Эйлера». Чем больше я знаю, Тем больше умею.

Цели урока:  формирование знаний о кругах Эйлера;  развить умение решать задачи, используя круги Эйлера;  развить любознательность.

Оборудование: проектор.

Структура урока

I. Организационный момент – 2 минуты. II. Проверка домашнего задания, с исправлением ошибок – 8 минут. III. Новый материал – 10 минут. IV. Первичное осмысление и применение изученного – 10 минут. V. Логическая разминка – 4 минуты. VI. Обобщение и систематизация полученных знаний – 5 минут. VII. Выставление оценок – 3 минуты. VIII. Задание на дом – 3 минуты.

ХОД УРОКА

I. ОРГАНИЗАЦИОННЫЙ МОМЕНТ. II. ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ.

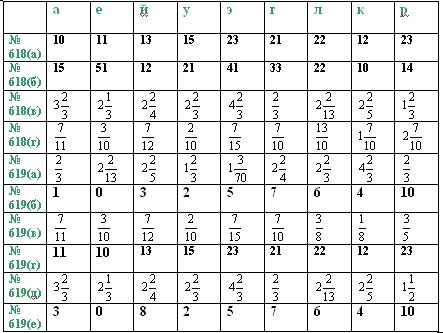
При проверки домашнего задания демонстрируется таблица через проектор.

Ответ: Круг Эйлера.

III. НОВЫЙ МАТЕРИАЛ. Сегодня мы познакомимся с новой для вас темой «Круги Эйлера», а также со способами применения их к решению задач. Круги Эйлера используются при решении задач. Этот метод дает более наглядное представление о возможном способе изображения условий, зависимости, отношений в логических задачах. Один из величайших математиков петербургский академик Леонард Эйлер за свою долгую жизнь (он родился в 1707 г., а умер в 1783 г.) написал более 850 научных работ. В одной из них и появились эти круги. Эйлер писал тогда, что «они очень подходят для того, чтобы облегчить наши размышления». Наряду с кругами в подобных задачах применяют прямоугольники и другие фигуры.

Разберём задачу используя метод кругов Эйлера: Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским - 28, французским - 42. Английским и немецким одновременно владеют 8 человек, английским и французским - 10, немецким и французским - 5, всеми тремя языками - 3. Сколько туристов не владеют ни одним языком?

Всеми тремя языками владеют три туриста, значит, в общей части кругов вписываем число 3. Английским и французским языками владеют 10 человек, а 3 из них владеют еще и немецким. Следовательно, только английским и французским владеют 10-3=7 человек. Аналогично получаем, что только английским и немецким владеют 8-3=5 человек, а немецким и французским 5-3=2 туриста. Вносим эти данные в соответствующие части.

Определим теперь, сколько человек владеют только одним из перечисленных языков. Немецкий знают 30 человек, но 5+3+2=10 из них владеют и другими языками, следовательно, только немецкий знают 20 человек. Аналогично получаем, что одним английским владеют 13 человек, а одним французским - 30 человек.

По условию задачи всего 100 туристов. 20+13+30+5+7+2+3=80 туристов знают хотя бы один язык, следовательно, 20 человек не владеют ни одним из данных языков. Ответ: только английским владеет 13 человек, только французским - 30, только немецким - 20 человек. 20 человек не знают ни одного из этих языков.

IV. ПЕРВИЧНОЕ ОСМЫСЛЕНИЕ И ПРИМЕНЕНИЕ ИЗУЧЕНОГО. Решение задачи в парах с применением новой темы (условие демонстрируется через проектор).

В классе 38 человек. Из них 16 играют в баскетбол, 17 - в хоккей, 18 - в футбол. Увлекаются двумя видами спорта - баскетболом и хоккеем - четверо, баскетболом и футболом - трое, футболом и хоккеем - пятеро. Трое не увлекаются ни баскетболом, ни хоккеем, ни футболом.

Сколько ребят увлекаются одновременно тремя видами спорта? Сколько ребят увлекается лишь одним из этих видов спорта?

Проверка выполнения задания (демонстрация через проектор). Воспользуемся кругами Эйлера.

Пусть большой круг изображает всех учащихся класса, а три меньших круга Б, Х и Ф изображают соответственно баскетболистов, хоккеистов и футболистов. Тогда фигура Z, общая часть кругов Б, Х и Ф, изображает ребят, увлекающихся тремя видами спорта. Из рассмотрения кругов Эйлера видно, что одним лишь видом спорта - баскетболом занимаются 16 - (4 + z + 3) = 9 - z; одним лишь хоккеем 17 - (4 + z + 5) = 8 - z; одним лишь футболом 18 - (3 + z + 5) = 10 - z. Составляем уравнение, пользуясь тем, что класс разбился на отдельные группы ребят; количества ребят в каждой группе обведены на рисунке рамочкам:

3 + (9 - z) + (8 - z) + (10 - z) + 4 + 3 + 5 + z = 38, z = 2. Таким образом, двое ребят увлекаются всеми тремя видами спорта. Складывая числа 9 - z, 8 - z и 10 - z, где z = 2, найдем количество ребят, увлекающихся лишь одним видом спорта: 21 человек. Ответ. Двое ребят увлекаются всеми тремя видами спорта человека. Увлекающихся лишь одним видом спорта: 21 человек.

V. ЛОГИЧЕСКАЯ РАЗМИНКА. Продолжить ряды тремя числами: 1, 5, 9, 13, … 0,2; 0,4; 0,8; 1,4… 18,5; 3,7; 0,74; 0,148;… VI. ОБОБЩЕНИЕ И СИСТЕМАТИЗАЦИЯ ПОЛУЧЕННЫХ ЗНАНИЙ. VII. ВЫСТАВЛЕНИЕ ОЦЕНОК. VIII. ЗАДАНИЕ НА ДОМ.