Семинар ДООМ Задачи, решаемые с помощью деревьев

Коннова Елена Генриевна ID_062,ID_063

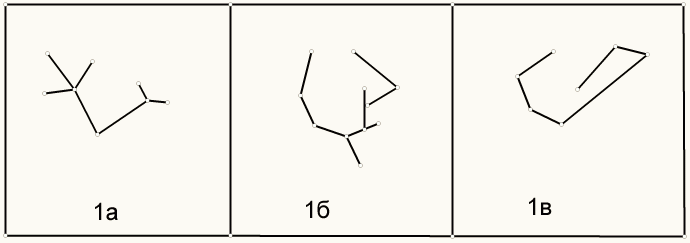
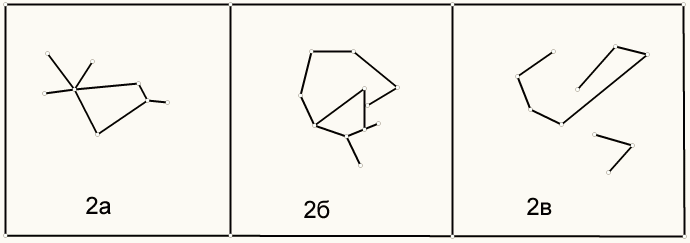
Деревом называется связный граф, не имеющий циклов. Примеры графов которые являются деревьями, приведены на рис. 1а,б,в. На рис. 2а,б,в изображены графы, но не деревья.

Напомним некоторые свойства дерева.

1. В дереве нельзя вернуться в исходную вершину, двигаясь по ребрам и проходя по одному ребру не более одного раза.

Доказательство.

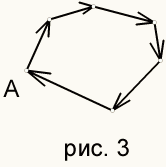
Предположим, что мы смогли это сделать. Выделим этот путь(см. рис. 3). Так как ребра не повторяются, то это цикл. Но в дереве не может быть циклов. Значит, сделать этого нельзя.

2. В дереве любые две вершины соединены ровно одним путем.

Доказательство.

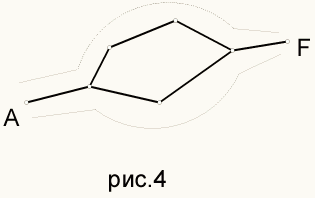
Пусть от одной вершины до другой два пути (см. рис. 4). Даже если начала путей совпадают, то где-то начнется "раздвоение", а раз у них общий конец, то есть вершина, где пути "сойдутся". Получится цикл, чего в дереве быть не может.

3. В дереве с n вершинами n-1 ребер.

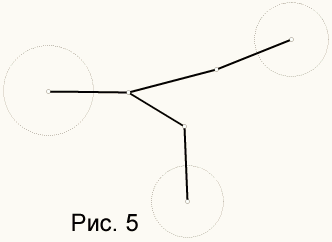
4. В дереве есть вершина, из которой выходит только одно ребро. Такая вершина называется висячей (см. рис. 5 - кругами выделены висячие вершины).

5. При удалении любого ребра из дерева он становится несвязным.

Доказательство.

Пусть мы удалили ребро между вершинами А и В, и граф остался связным. Значит, в получившемся графе есть путь из А в В. Но в первоначальном графе был еще путь АВ по удаленному ребру, а в дереве любые две вершины соединены ровно одним путем.

Признаки дерева - то есть те свойства графа, по которым мы можем определить, что граф - дерево.

1. Если граф связный и в нем нет циклов, то граф - дерево.

2. Если у связного графа число ребер на один меньше числа вершин, то граф - дерево.

3. Если в графе любые две вершины соединены ровно одним простым путем (таким, в котором ребра не повторяются), то граф - дерево.

Доказательство.

Такой граф связный. Докажем, что в нем нет циклов. Пусть цикл есть. Тогда между любыми двумя вершинами этого цикла есть два пути, а это противоречит условию. Значит, граф связный и не содержит циклов, это дерево.

Задачи.

1. В государстве Океания 17 островов, между ними проложены маршруты так, что с каждого острова выходит ровно четыре маршрута. Докажите, что в Океании есть такие два острова, что с одного до другого можно добраться двумя разными путями (но может быть с пересадками на других островах).

Решение задачи 1.

Представим себе острова вершинами графа, а маршруты - ребрами этого графа. В этом графе сумма степеней вершин равна 17*4 и значит в нем 17*4:2= 34 ребра. Если в этом графе есть цикл, то между любыми вершинами цикла есть два пути - с противоположным направлением обхода. Если же циклов в этом графе нет, то граф является деревом или состоит из нескольких деревьев, а в любом дереве число ребер на 1 меньше числа вершин. Но у нас в графе ребер больше чем вершин, значит в графе есть цикл.

2. На острове - столице Океании 53 дома, некоторые из которых соединены дорогами, и любые два города соединяет ровно один путь. Сколько дорог в столице Океании?

Решение задачи 2.

Пусть дома будут вершинами графа, а маршруты - ребрами этого графа. В этом графе любые два города соединяет ровно один путь, значит граф является деревом. В дереве вершин на 1 больше, чем ребер, значит дорог на 1 меньше, чем домов, значит их 52.

3. В 2007 году водное сообщение между 17 островами Океании стало невозможным из-за нашествия акул. Правительство организовало воздушное сообщение так, чтобы с любого острова можно было попасть на любой другой (но, может быть, с пересадками). Было проложено 16 маршрутов. Докажите, что если один маршрут закрыть, то найдется остров, с которого нельзя будет добраться до столицы (столица расположена на одном острове).

Решение задачи 3.

Пусть острова - вершины графа, а ребра - маршруты. Так как с любого острова можно попасть на любой другой, то граф связный, в нем 17 вершин и 16 ребер, ребер на 1 меньше, значит это дерево. Если один маршрут закрыть (удалить одно ребро из дерева), то граф станет несвязным. Тогда рассмотрим вершину (остров) из той компоненты связности, в которую не входит столица. С этого острова нельзя будет добраться до столицы.

4. Маша и Саша любят играть в такую игру: в рыболовной прямоугольной сетке размером 4х5 ячеек по очереди перерезают по одной веревочке так, чтобы сетка не распалась на куски. Победитель тот, кто разрежет последнюю веревочку. Кто выиграет при правильной игре?

Решение задачи 4.

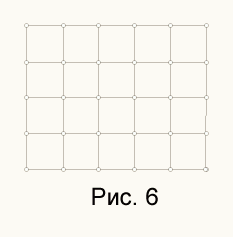
Представим узлы сетки вершинами, а веревочки - ребрами графа. В начале игры было 5*6 вершин и 5*5+4*6=49 ребер (см. рис. 6).

Можно удалять ребра до тех пор, пока в графе остались циклы. Как только граф станет деревом, при удалении любого ребра он перестанет быть связным, и игрок не сможет сделать ход. Вершин при этом осталось 30, значит ребер стало 30-1=29. За игру будет удалено 49-29=20 ребер, значит последний ход сделает второй игрок и выиграет.

5. В Океании объявили конкурс: в куске сетки размером 5x20 ячеек нужно перерезать как можно больше веревочек так, чтобы сетка не распалась на куски. Победитель получит приз. Какое наибольшее число веревочек можно перерезать?

Решение задачи 5.

Если представить узлы сетки вершинами, а веревочки - ребрами графа, то в этом графе нужно удалить как можно больше ребер так, чтобы он остался связным. До разрезания было 6*20+21*5=205 ребер- веревочек. Можно удалять ребра до тех пор, пока не останется граф без цикла. При этом из цикла любое ребро можно удалить, и граф при этом останется связным. Связный граф, в котором нет циклов, дерево, в нем 6*21 вершина и соответственно 6*21 - 1= 125 ребер. Больше ребер удалять нельзя, тогда из дерева получится несвязный граф. Значит, можно удалить 205- 125=180 ребер.