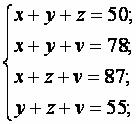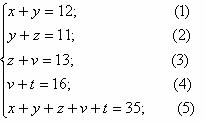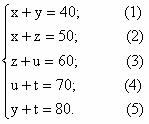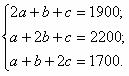Семинар ДООМ Задачи на составление систем с числом уравнений больше двух

Цепенкова Ирина Павловна. ЗВЕЗДА ID 248 Цепенкова Ирина Павловна

Здравствуйте, уважаемые участники методического семинара.

Всем известно, что учебник математики, даже самый замечательный, не может охватить огромное разнообразие текстовых задач. А так хочется разнообразить уроки нестандартными задачками. На уроках математики и в качестве дополнительных домашних задач я предлагаю ребятам задачи на составление систем с числом уравнений больше двух. Знакомить ребят с этими задачами необходимо, они предлагаются учащимся на олимпиадах. Сюжет задачи позволяет привлечь учащихся к анализу условия, составлению системы уравнений и поиску решения этой системы.

Задача 1

Таня купила в магазине шариковую ручку, карандаш, тетрадь и альбом для рисования. Ручка, карандаш и тетрадь вместе стоят 50 коп. Ручка, карандаш и альбом стоят вместе 78 коп, а карандаш, тетрадь и альбом – 55 коп. Сколько стоит каждый предмет в отдельности?

Решение:

Пусть ручка стоит х коп., карандаш – у коп., тетрадь – z коп., альбом – v коп. Составим и решим систему уравнений.

Сложив, уравнения, получим 3x + 3y + 3z + 3v =270.

Откуда x + y + z + v = 90.

От полученного уравнения отнимем последовательно каждое уравнение системы. Получим:

(x + y + z + v) – (x + y + z) = 90 – 50; v = 40;

(x + y + z + v) – (x + y + v) = 90 – 78; z = 12;

(x + y + z + v) – (x + z + v) = 90 – 87; y =3;

(x + y + z + v) – (y + z + v) = 90 - 55; x =35.

Ответ: ручка стоит 35 коп., карандаш – 3 коп., тетрадь – 12 коп., альбом – 40 коп.

Задача 2

От города А до города В по прямой дороге 35 км, На пути расположены 4 автобусных остановки. Зная, что расстояние от города А до второй остановки 12 км, от первой остановки до третьей – 11 км, от второй остановки до четвёртой – 12 км, от третьей остановки до города В – 16 км. Найдите расстояние от города А до первой остановки, от первой остановки до второй, от второй до третьей, от третьей до четвёртой и от четвёртой до города В.

Решение:

Сделаем чертёж и введём обозначение неизвестных.

.

Пусть АС – x км, СD – y км, DE – z км, EF – v км, FB – t км. По условию задачи составим систему уравнений.

Сложим уравнения (1) и (4): x + y + v + t = 28.

Сравним с уравнением (5):(x + y + v + t) + z = 35

28 + z = 35;

z =7.

Тогда из (2) получим y + 7 =11; y = 4.

Из (1) следует x + 4 =12; x = 8;

Из (3) получим 7 +v = 12; v = 5;

Из (4) получим 5 + t = 16; t =11.

Ответ: расстояние от города А до первой остановки 8 км, от первой остановки до второй – 4 км, от второй до третьей – 7 км, от третьей до четвёртой – 5 км, от четвёртой до города В – 11 км.

Задача 3

Катя и Маша вместе весят 40 кг, Катя и Света – 50 кг, Даша и Галя – 80 кг. Сколько весит каждая девочка?

Решение

Пусть Катя весит х кг, Маша – y кг, Света – z кг, Даша – u кг, Галя – t кг. Составим и решим систему уравнений.

Каждая буква в системе повторяется два раза. Сложим все уравнения, получим:

2(x + y + z + u + t) = 300;

x + y + z + u + t = 150. (6)

Обозначим это уравнение (6). В него вошли все пять неизвестных. Теперь будем складывать уравнения так, чтобы в сумму вошли 4 неизвестных по одному. И из уравнении (6) будем вычитать уравнения, полученные от сложения по два. Сложим (1) и (3), получим x + y + z + u =100. Из (6) вычтем полученное равенство

(x + y + z + u + t) - (x + y + z + u) = 150 - 100; t = 50.

Подставим t = 50 в (5): y +50 =80; y = 30;

в (1): x + 30 = 40; x = 10;

в (2): 10 + z = 50; z = 40;

в (3): 40 + u = 60; u = 20.

Ответ: Катя = 10 кг, Маша – 30 кг, Света – 40 кг, Даша – 20 кг, Галя – 50 кг.

Задача 4

Две пачки печенья, пачка сахара, банка варенья имеют массу 1 кг 900 г. Масса одной пачки печенья, двух пачек сахара и банки варенья 2 кг 200 г, а одной пачки печенья, пачки сахара и двух банок варенья 2 кг 700 г. Определите общую массу трёх банок варенья, четырёх пачек печенья и трёх пачек сахара.

Решение:

Пусть масса 1 пачки печенья – а г, 1 пачки сахара – b г, 1 банки варенья – г. Составим и решим систему уравнений.

После сложения уравнений получим: 4a + 4b + 4c = 6800 т. е. a + b + c = 1700. Далее находим: а = 200; b = 500; c = 1000. Тогда масса трёх банок варенья, трёх пачек сахара и четырёх пачек печенья вместе 5 кг 300 г.

Несколько задач без решения, но с ответами:

Задача 6

В двух комнатах было 76 человек. Когда из одной комнаты вышли 30, а из второй 40, то людей в комнатах осталось поровну. Сколько человек было в каждой комнате первоначально?

(Ответ: 33, 43 человека).

Задача 7

На трёх полках 30 книг. На первой и второй 14 книг, на второй и третьей – 15. Сколько книг на каждой полке?

(Ответ: 15, 7, 8).

Задача 8

Пять учеников купили 100 тетрадей. Катя и Вася – 52 тетради, Вася и Юра – 43, Юра и Саша – 34, Саша и Серёжа – 30. Сколько тетрадей купил каждый из них?

(Ответ: Юра – 18, Вася – 25, Коля – 27, Саша – 16, Серёжа - 14).

Задача 9

На лугу паслись 90 телят и гусей. Всего у них было 256 ног. Сколько было телят и сколько гусей?

(Ответ: 38 телят, 52 гуся).

Желаю Всем удачи!.