Семинар ДООМ Методика работы над условием задачи

Решение сюжетной задачи один из самых важных вопросов математики. Чтобы понять условие задачи, я всегда прошу детей записать краткое ее содержание. В своей практике приходилось сталкиваться с тем, что не все учителя отдают этому вопросу должное внимание. Поэтому мне хочется поделиться своими соображениями, опираясь на свой опыт и на работы других педагогов.

Решение каждой математической задачи осуществляется, вообще говоря, по четырем основным этапам:
1. понимание условия и требования задачи; ясное усвоение и осмысливание отдельных элементов условия;
2. составление плана решения;
3. практическая реализация плана во всех его деталях;
4. окончательное рассмотрение задачи и ее решения с целью усвоения тех моментов, которые могут стать полезными для дальнейшего решения задач.

Остановимся на рассмотрении только наиболее важных вопросов, связанных с реализацией этих этапов. Особое внимание учитель должен уделить первому этапу решения. Часто поиск учащимся правильного решения задачи обрывается именно в самом начале, учащийся теряет веру в свои силы.
Поэтому, прежде чем непосредственно приступать к решению задачи, нужно охватить условие задачи в целом, вжиться в нее, суметь отметить ее особенности, наметить в общих чертах возможные направления решения и вспомнить относящиеся к этим направлениям разделы теории.
Все это поможет учащимся в правильном выборе пути решения. Даже при решении простой задачи учащиеся нередко дают утвердительный ответ на ее вопрос. Это можно объяснить лишь тем, что они не вникли в условие задачи, поспешили ответить, не вспомнили соответствующий вопросу раздел теории.
Таким образом, отсутствие должного внимания к работе на первом этапе решения может сразу привести к ошибочному результату. Для выработки правильного понимания школьниками поставленной задачи можно рекомендовать соблюдение следующих требований.
1. Начинайте изучение условия задачи с аккуратно выполненных и наглядных чертежей или иллюстративных схем. Помните, что правильное графическое представление условия задачи означает по существу четкое, ясное и конкретное представление о всей задачной ситуации в целом.
2. Представьте ясно и детально все основное, связанное с данной задачей. Обстоятельно выясните, что дано, что надо найти; выделите при этом главное в тексте условия задачи и сконцентрируйте на нем свое внимание. Выделите на чертеже данные и искомые величины различными яркими цветами.
3. Проверьте тщательно каждое выдвигаемое в процессе решения задачи положение контрольными вопросами вида: что это означает, какие имеются основания для данного утверждения, какую пользу можно извлечь из данного факта?
4. Проверьте, однозначно ли сформулирована задача. Нет ли в условии задачи избыточных или недостающих данных?
Результаты предварительного анализа задач надо как-то зафиксировать, записать. Надо найти более удобную, компактную и в то же время достаточно наглядную форму записи результатов анализа задач. Такой формой является схематическая запись задачи.
Не для всякой задачи надо делать схематическую запись. Так, например, для задач по решению уравнений, неравенств, преобразований выражений анализ проводится обычно устно и никак не оформляется. Вообще для задач, которые записаны на символическом языке (с помощью общепринятых обозначений и символов), схематическая запись не нужна.
Первой отличительной особенностью схематической записи задач является широкое использование в ней разного рода обозначений, символов, букв, рисунков, чертежей. Вторая особенность заключается в том, что в ней четко выделены все условия и требования задачи, а в записи каждого условия указаны объекты и их характеристики, наконец, в схематической записи фиксируется лишь только то, что необходимо для решения задачи; все другие подробности, имеющиеся в задаче, при схематической записи отбрасываются.
На практике используется много разных видов схематической записи задач. Покажем на примерах.

Задача 1. С одного участка, собрали 1440 ц пшеницы, а с другого, площадь которого на 12 га меньше,—1080 ц. Найти площадь первого участка, если известно, что на первом участке собирали пшеницы с каждого гектара на 2 ц больше, чем на втором.

Анализ задачи показывает, что в ней рассматривается сбор урожая пшеницы с двух участков, при этом этот сбор характеризуется тремя величинами: массой собранной пшеницы, площадью участка и урожаем с одного гектара. Исходя из этого, составим таблицу для схематической записи условий и требований задачи. Неизвестные величины, встречающиеся в задаче, запишем в таблице буквами х и у:

Участки	Масса собранной пшеницы, ц	урожай с 1 га, ц	Площадь участка, га
Первый	1440 или (у + 2) х	у + 2	х
Второй	1080 или у(х — 12)	у	х — 12

В этой схематической записи выделены все условия, их объекты и характеристики. Указано и требование задачи: найти площадь первого участка. В то же время эта запись очень компактная, наглядная и полностью заменяет саму формулировку задач, помогает составить систему уравнений.

Задача 2. Скорый поезд должен по расписанию пройти перегон АВ без остановок за 4 ч. Однако в 150 км от станции А он был задержан на 20 мин и, чтобы прибыть на станцию В по расписанию, должен был пройти оставшийся путь со скоростью, превышающей первоначальную на 15 км/ч. Найти длину перегона АВ.

Участки	скорость, км/ч	время, ч	расстояние, км
по расписанию	х	4	4х
первый	х	150/х	150
второй	х + 15	4х – 150)/( х + 15)	4х – 150

Зная общее время и время задержки, можно составить уравнение 150/х + (4х – 150)/( х + 15)+ 1/3 = 4.

Задача 3. Первый рабочий может выполнить некоторую работу за 8 дней, второй – за 12 дней. К выполнению работы оба рабочих приступили одновременно и проработали вместе некоторое число дней, после чего второй рабочий был переведен на другую работу. Оставшуюся часть работы закон-чил один первый рабочий за три дня. Сколько всего дней работал первый рабочий?
В таких задачах объем работы принимаем за 1.

		первый	второй
По плану	кол-во дней	8	12
	производительность	1/8	1/12
	объем работы	1	1
Работали совместно
	кол-во дней	х	х
	объем работы	1/8 х	1/12 х
	Работал один
	кол-во дней	3
	объем работы	1 – (1/8 х + 1/12 х)
	производительность	(1 – (1/8 х + 1/12 х))/3 или 1/8

Согласимся с тем, что не каждый ученик сможет составить такую таблицу. Учитель, показывая, как идет рассуждение при анализе условия задачи, учит детей вжиться в созданную ситуацию.

Использование чертежей для схематической записи задач.

Довольно часто удобно составлять схематическую запись не для всей задачи, а лишь для какой-либо ее части, чтобы более наглядно представлять описываемую в задаче ситуацию, а так же чтобы в решении оперировать теми обозначениями, которые вводятся в этой частичной схематической записи. В этих случаях используются разного рода графические схемы. Приведем пример.

Задача 4. От станции А по направлению к станции В отошел пассажирский поезд. Через 2 ч 30 мин от станции В по направлению к станции А отошел поезд «Стрела». Поезда встретились на станции С. После встречи пассажирский поезд шел 4 ч 30 мин, а поезд «Стрела» 3 ч 40 мин. Сколько времени потребовалось каждому из этих поездов на весь путь между станциями А и В? Предполагается, что скорость поездов постоянна на всем пути. Изобразим схему движения поездов (рис. 1).

Приведенная схема сама по себе не может полностью заменить задачу. Она лишь создает возможность опираться на нее, как на наглядный образ, при решении.
Задание для самостоятельной работы.
Составьте для приведенных задач схематические записи (полные или частичные).
1. Одна мастерская должна была изготовить 420 деталей; другая за тот же срок 500 деталей. Первая выполнила свою работу на 4 дня раньше срока, а вторая на 7 дней. По скольку деталей в день изго-товляла каждая мастерская, если вторая мастерская ежедневно изготовляла на 5 деталей больше?
2. Из А в С вышел пешеход. Спустя 1 ч 24 мин в том же направлении из А выехал велосипедист и через 1 ч ему оставалось проехать 1 км, чтобы догнать пешехода, а еще через 1 ч велосипедисту оставалось проехать до С вдвое меньше расстояние, чем пройти пешеходу до С. Найти скорости пешехода и велосипедиста, если известно, что расстояние АС равно 27 км.

Для схематической записи геометрических и некоторых других задач полезно использовать чертеж той фигуры, которая рассматривается в задаче. При построении такого чертежа надо выпол¬нять ряд требований. Укажем главные из них.
1. Чертеж должен представлять собой схематический рисунок основного объекта задачи (геометрической фигуры, или совокупности фигур, или какой-то части этих фигур) с обозначением с помощью букв и других знаков всех элементов фигуры и некоторых их характеристик. Если в тексте задачи указаны какие-либо обозначения фигуры или ее элементов, то эти обозначения должны быть и на чертеже; если же в задаче никаких обозначений нет, то следует воспользоваться общепринятыми обозначениями или придумать наиболее удобные.
2. Этот чертеж должен соответствовать задаче. Это означает, что если в задаче в качестве основного объекта назван, например, треугольник и при этом не указан его вид (прямоугольный, равносторонний и др.), то надо построить какой-либо разносторонний треугольник. Или если в задаче в качестве основного объекта названа трапеция и не указан ее вид, то не следует строить равнобедренную или прямоугольную трапецию и т.д.
3. При построении чертежа нет надобности выдерживать строго какой-либо определенный масштаб. Однако желательно соблюдать какие-то пропорции в построении отдельных элементов фигуры. Например, если по условию задачи сторона АВ треугольника ABC наибольшая, то это должно быть соблюдено на чертеже. Или если задана медиана треугольника, то соответствующий ей отрезок на чертеже должен проходить приблизительно через середину стороны треугольника и т. д.
Точно так же надо соблюдать на чертеже такие отношения, как параллельность, перпендикулярность и другие, заданные в задаче.
4. При построении чертежей пространственных фигур необходимо соблюдать все правила черчения. Там, где это можно и целесообразно, лучше строить какие-либо плоскостные сечения этих фигур.
Говоря о первом из этих требований, отметим, что оно особенно важно при решении геометрических задач, где наглядный и четкий чертеж позволяет иной раз с первого же взгляда обнаружить возможные пути решения. Чертежи при решении геометрических задач надо делать не только аккуратно, но и грамотно. Нередко в работах учащихся встречаются ошибки, связанные с неграмотностью в по-строении чертежа. Чертежи по условию данной задачи не должны быть мелкими. Полезно, по возможности, следить за соблюдением масштаба в изображении данных величин и особенно масштаба, отвечающего реальному соотношению данных величин друг с другом. Следует предостеречь учащихся от сведения общих случаев к частным (например, когда вместо произвольного треугольника выполняется чертеж равностороннего треугольника), так как в результате несоблюдения этого требования можно прийти к ложным выводам.
Полезно хорошо продумать расположение всех элементов на эскизе чертежа; полезно перемещать отдельные элементы фигуры, рассматривая фигуру в новом положении. В противном случае так-же нередки ложные выводы.

Кроме чертежа, для схематической записи геометрических задач используется еще краткая запись всех условий и требований задачи. В этой краткой записи, пользуясь принятыми на чертеже обозначениями, записываются все характеристики и отношения, указанные в условиях задачи. Названия фигур или отдельных ее частей желательно заменять записью их определений. Например, вместо того чтобы писать: ABCD — трапеция, можно писать: AB || CD.
В краткой записи можно использовать, там, где это целесообразно, стандартные математические знаки (принадлежности элемента к множеству, параллельности, перпендикулярности и т. д.). Конечно, все приведенные рекомендации имеют не всеобщий характер, и при решении отдельных геометрических задач чертеж фигур и краткая запись условия могут производиться иначе.
Рассмотрим на примерах, как строятся схематические записи, геометрических задач с помощью чертежей.
Задача 5. Диагональ трапеции перпендикулярна к ее основаниям; тупой угол, прилежащий к большему основанию, равен 120°, а боковая сторона, прилежащая к нему, равна 7 см; большее основание равно 12 см. Найти среднюю линию трапеции.

Основным объектом этой задачи является трапеция. В этой трапеции одна из диагоналей перпендикулярна к ее основаниям. Если вы начнете чертить эту трапецию обычным способом, т. е. начиная с построения ее сторон, то обязательно ошибетесь (проверьте: попробуйте, не читая последующие строки, начертить заданную трапецию, начиная с построения ее оснований и боковых сторон). Лучше начать с построения указанной диагонали. Обратите внимание на то, что эта диагональ перпендикулярна к обеим основаниям трапеции. Это можно представить так: диагональ — это вертикальный отрезок, от концов которого отходят два горизонтальных отрезка (основания трапеции), притом в разные стороны.

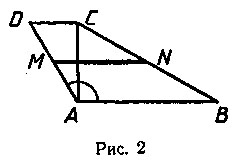
Когда вы это построите, то тогда вам станет ясно, что углы трапеции у вершин, которые соединяет эта диагональ, должны быть оба тупыми. Действительно, в задаче дано, что угол при большем основании равен 120°. Это должен быть как раз тот угол, вершина которого есть один из концов построенной диагонали. Теперь уже построить заданную трапецию нетрудно. Обозначим ее вершины, заданный угол отметим дугой и проведем среднюю линию. Пользуясь принятыми на чертеже обозначениями, запишем все условия и требование задачи. Получаем такую схематическую запись задачи (рис. 2).

Немаловажную роль в успешном решении задач играет целенаправленность поиска решения, т. е. сознательное ограничение числа проб и ошибок, характерных для начальной его стадии.
Иногда учащийся не в состоянии самостоятельно проанализировать задачу и решить ее без помощи учителя. Однако в этом случае трудно переоценить роль учителя в математическом развитии ребят. Именно благодаря творческому труду учителя, умению доходчиво, на хорошем научном уровне объяснить новый материал, умению правильно подобрать задачи возможно всестороннее развитие матема-тического мышления учащихся.
Чем же должен руководствоваться учитель при подборе учебных задач?

Рассмотрим памятку для анализа педагогической ценности задачи:

 Какую учебную цель преследует данная задача?
 Какие элементы математического образования имеются в виду?
 Необходима ли именно эта задача?
 Почему такие, а не другие конкретные величины взяты в задаче?
 Почему выбрана такая именно фабула задачи?
 Почему взяты такие, а не другие числовые данные?
 Отвечают ли числовые данные реальной обстановке, в которой могла бы возникнуть аналогичная задача?
 Интересна ли фабула задачи для учащихся, увлекательна, естественна ли постановка вопроса, вызывает ли она у учащихся интерес к ответу или способу решения, чем именно?
 Сможет ли учащийся самостоятельно решить данную задачу? Что он для этого должен знать, помнить, уметь, представлять себе? Если учащийся не сможет этого сделать, о чем будет свидетельствовать этот факт?
 Чем и в какой мере ему может и должен помочь учитель?  Как эта задача связана с предшествующей и последующей учебной работой учащегося? И т. д.

Давая такую оценку каждой учебной задаче, учитель сумеет при минимальной затрате учебного времени добиться хороших результатов как в обучении, так и в развитии математического мышления школьников.
Но учитель не только должен сам уметь оценивать задачу, выявляя все ее полезные учебные качества, он должен научить этому учащихся.
Даже очень хорошие учащиеся, получив ответ на вопрос задачи и тщательно изложив ход ее решения, закрывают тетрадь, полагая работу законченной. Учитель обязан понимать, что никакую задачу нельзя исчерпать до конца. Этот взгляд он должен прививать и своим ученикам. Всегда остается что-нибудь, над чем можно и нужно поразмышлять; всегда можно усовершенствовать любое решение, глубже его осмыслить, выявить полезную и новую для учащихся информацию. Поэтому после решения каждой задачи следует еще раз оглянуться назад, обратить внимание на метод, который был ис-пользован, попытаться найти другие пути решения, выявить то, что необходимо помнить.

Литература.

1. Методика преподавания математики в средней школе. Ю.М.Колягин и др. Москва, «Просвещение», 1975 год.
2. Как научиться решать задачи. Л.М.Фридман, Е.Н.Турецкий. Москва, «Просвещение», 1989 год.
3. Как решать задачу. Д.Пойа. Львов, журнал «Квантор». 1991 год
4. Решение задач в курсе арифметики 5-6 классов средней школы. П.В.Стратилатов. Москва, Учпедгиз, 1963 год