Семинар ДООМ Применение логических задач в 5-6 классах
Участник:Хайруллина Гульнара Равильевна
Проведение всевозможных олимпиад и марафонов приводит учителя к необходимости искать нестандартные задачи. В этой статье такая подборка задач, которая помогает развивать способности ребят рассуждать, логически мыслить; помогает вырабатывать отношение к математике, как к красивой точной науке. Логические задачи достаточно интересны и очень полезны для развития математических способностей. Они вырабатывают умение устанавливать связи между объектами, наблюдательность, настойчивость. Однако при решении таких задач ученики много времени тратят на рассуждения о том, с чего начать. Поэтому полезна следующая подборка задач.
Степень сложности возрастает постепенно от задачи к задаче. Предлагаемые задачи собраны из разных учебных пособий и периодической печати. Все задачи решены или имеют советы по их решению.
В последней третьей части многочисленные факты, содержащиеся в условии, ребята легко воспринимают с помощью схем или «графов». Принцип их построения доступен каждому: объекты изображаем точками, а отношения между ними – отрезками; точки соединяем сплошной линией, если точки одного множества соответствуют точкам другого множества, или штриховой, если они не соответствуют. С помощью такого наглядного приёма можно научить пятиклассников решать достаточно сложные задачи.
Не торопитесь помочь ученику решить их, если он в состоянии сделать это сам. Пусть ребята учатся думать, искать решение, даже если они сначала не видят плана действий.
« Плохой учитель преподносит истину, хороший учит её находить.» Дистерверг
Содержание[убрать] |
Часть І
1. На каком расстоянии от точки О на отрезке ОД надо отметить точку С , чтобы сумма длин отрезков ОС и СД была наименьшей, если ОД=6 см?
2. От домика паучка Ку до домика паучка Кэ ведёт прямая дорога. Расстояние между домиками Ку и Кэ 13 м. Куда бы эти паучки не ползли, за ними всегда тянется ниточка паутины. В каком месте дороги паучкам лучше встретиться, чтобы сумма длин их ниточек оказалась наименьшей?
3. Если Ку ползёт к Кэ не один, а со своей сестрой Ка ( см. задачу 2), за которой тоже тянется паутинка, то где им лучше всего назначить место встречи, чтобы сумма длин всех трёх паутинок была наименьшей?
4. В деревне Цут живет 100 паучков-учеников, а в деревне Цат – 50 паучков- учеников. На каком расстоянии от деревни Цут( на дороге, соединяющей эти деревни) надо строить школу для паучков, чтобы сумма длин всех паутинок, которые сплетут 150 паучков после того, как выйдут на дорогу до школы, была наименьшей? Длина дороги 10 м.
Часть І І
1. Ребята заметили , что участок ветки в 15 см гусеница проползла за 7 минут. Найдите длину гусеницы, если скорость её движения 3см/мин .
2. Поезд длиной 450 м проходит мост за 35 с, а мимо дежурного по станции проходит за 15 с. Найдите длину моста и скорость поезда.
3. Поезд проходит мост длиной 450 м за 45 с, а мимо светофора- за 15 с. Найдите длину поезда и его скорость .
4. Поезд, длиной 18 м, проезжает мимо столба за 9 с. Найдите время, за которое поезд проедет мост длиной 36м.
Часть І І І (нужно использовать при подготовке к ДООМ по теме «Тайна графов»)
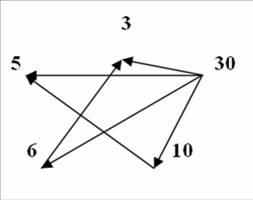
1. А={ 3;5;6;10;30}, a є А , b є А . Найдите все пары ( a ; b ), где a : b и a≠b.
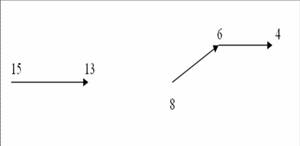
2. М={ 4;6;8;13;15}, k є М , a є М . Найдите все пары ( k ; a ), где k-a=2.
3. Несколько зайчиков встретились на опушке. Каждый с каждым поздоровался за лапу. Сколько было зайчиков, если было 10 лапопожатий ?
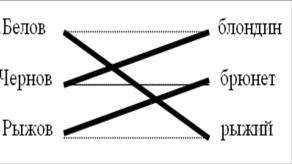
4. Встретились Белов, Чернов и Рыжов .Один из них был блондин, другой- брюнет, третий- рыжий .Брюнет сказал Белову: «Ни у одного из нас цвет волос не соответствует фамилии». Какой цвет волос у каждого из них, если брюнеты всегда говорят правду?
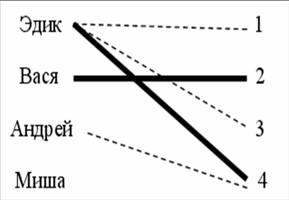
5. Эдик, Вася, Андрей и Миша заняли первые четыре места в соревнованиях, причем ни на одно призовое место не было двух претендентов. На вопрос какие они заняли места, мальчики честно ответили: 1) Андрей - « Я не был последним»;2) Вася - « Я занял второе место»; 3) Эдик - « Я занял ни первое и ни третье место». Какие места заняли мальчики?
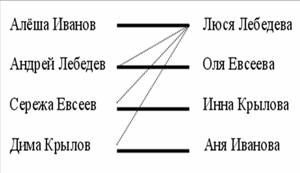
6. Четыре подруги вышли на каток, каждая со своим братом. Они разбились на пары и начали кататься. Оказалось, что в каждой паре партнер выше своей партнерши и никто не катается со своей сестрой. Самый высокий из компании - Алёша Иванов , следующий по росту- Андрей Лебедев, а затем Люся Лебедева, Серёжа Евсеев, Оля Евсеева, Дима Крылов, Инна Крылова и Аня Иванова .Кто с кем катался?
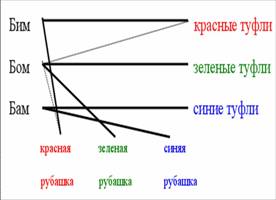
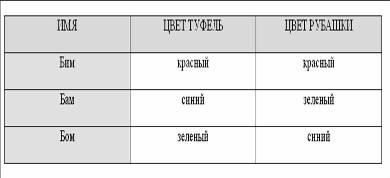
7. Три клоуна Бим , Бом и Бам вышли на арену в красной, зелёной и синей рубашках. Их туфли были трёх же цветов. У Бима цвета рубашки и туфель совпадали. У Бома ни туфли , ни рубашка не были красными . Бам был в зелёных туфлях, но в рубашке другого цвета. Как были одеты клоуны?
РЕШЕНИЯ И УКАЗАНИЯ
Часть І
1. Точка С может совпадать с О или точкой Д, а может находиться где угодно между ними: ОС+СД=ОД.
2. Всё равно.
3. Если бы ползали вдвоём , как в задаче 2,то сумма длин паутинок была равна 13 м, независимо от места встречи. Теперь эта сумма будет увеличиваться на длину паутинки Ка, следовательно, чем дальше от домика Ку и Ка паучки встретятся , тем больше сумма длин паутинок. Чтобы эта сумма была наименьшей, Ку и Ка надо встретиться с Кэ прямо в своем домике.
4. Школу надо построить в деревне Цут.
Часть І І
1. Ребята обязательно должны решать задачу с рисунком. Имеем: 3• 7= 21 (см) «проползет» голова гусеницы за 7 минут, значит, 21см- это длина ветки и длина гусеницы, следовательно, длина гусеницы 21-15= 6 см.
2. 1) 450: 15= 30( м/с)-скорость поезда;
2)30•35=1050(м)-расстояние,пройденное поездом за 35с ;
3)1050-450=600(м) - длина моста (так как 1050м-это длина моста и длина поезда).
3. За 45 секунд поезд проходит расстояние, равное длине моста и длине поезда вместе. Следовательно, длину моста ( 450м) он проходит за 30 с , то есть его скорость:450:30=15 (м/с). «Свою длину» поезд «протягивает» мимо светофора за 15с со скоростью 15 м/с, значит, его длина 15 • 15=225 ( м).
4. 18 : 9 = 2 ( м/с)- скорость поезда. « Голова» поезда проезжает мост, значит и длину поезда. Имеем: 36+18=54 (м), 54:2 =27(сек)
Часть І І І
1. (6;3),(10;5),(30;3), (30;5), (30;10), (30;6).
2. (6;4), (8;6), (15;13).
3. 2 зайчика – 1 лапопожатие, 3 зайчика – 1+2=3 лапопожатия, 4 зайчика – (1+2)+3=6 лапопожатий,
5 зайчиков – (1+2+3)+4= 10 лапопожатий.
4.
5. Эдик мог занять только 4-е место, Андрей- 1-е или 3-е, тогда Миша- 3-е или 1-е.
6. Люся Лебедева может танцевать только с Алёшей Ивановым, так как Андрей Лебедев её брат, а Серёжа и Дима ниже ростом. Рассуждая аналогично, делаем вывод, что Оля танцует с Андреем, Инна- с Серёжей, Аня- с Димой.
7. Жирными линиями обозначим условие:
Бом может быть только в синих туфлях, тогда Бим в красных туфлях и в красной рубашке. Теперь Бам может быть только в синей рубашке, тогда Бом в зеленой. Итак:
Используемая литература:
1. МАТЕМАТИКА ,еженедельная учебно-методическая газета №7-2004год, издательский дом 1 сентября;
2. Внеклассная работа по математике, библиотечка учителя, З. Н. Альхова, А. В. Макеева, из-во «Лицей» 2001год.