Семинар ДООМ Разработка факультативного занятия в 9 классе по теме "Графы"
Вохминцева Галина Сергеевна ID_103
Тема: Графы помогают решать задачи
Цель занятия:
- Рассмотреть типы задач на отыскание путей через лабиринты
- Научиться применять эйлеровы графы к решению задач.
- Прививать интерес к математике средствами теории графов
I. Практическая работа
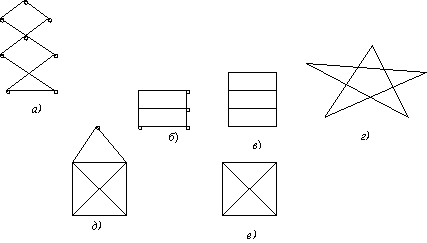
На столах учащихся лист с заданием: Попробуйте обвести изображение графов, представленных на рисунке, не отрывая карандаша от бумаги и не проводя уже по обведенному ребру вторично.
Задания по обведению ребер удается выполнить для графов на рисунке (а) б) г) д)), а для графов в), е) этого сделать нельзя. В чем секрет? Какие свойства графа повлияли на это?
II. Изучение нового материала
Изложение материала осуществляет учитель • Эйлеровым путем в графе называется путь, содержащий все ребра графа. • Эйлеровым циклом в графе называется цикл, содержащий все ребра графа. • Граф, обладающий эйлеровым циклом, называется эйлеровым графом.
Принято всякую замкнутую линию, если ее можно начертить, не отрывая карандаша от бумаги, проходя при этом каждый участок в точности один раз, называется уникурсальной.
Рисунок графа, обладающего эйлеровым путем или эйлеровым циклом, является уникурсальной линией.
Теорема 1. Если граф обладает эйлеровым циклом, то он связный и все его вершины четные.
Доказательство. Связность графа следует из определения эйлерового цикла. Эйлеров цикл содержит каждое ребро и притом только один раз, поэтому, сколько раз эйлеров путь приведет конец карандаша в вершину, столько и выведет, причем уже по другому ребру. Следовательно, степень каждой вершины графа должна состоять из двух одинаковых слагаемых: одно – результат подсчетов входов в вершины, другое – выходов. Верно и обратное утверждение.
Теорема 2: Если граф связный и все его вершины четные, то он обладает эйлеровым циклом.
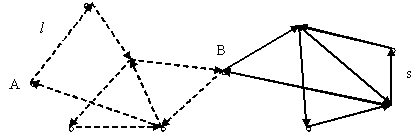
Доказательство. Если начать путь из произвольной вершины графа, то найдется цикл, содержащий все ребра графа. Пусть А – произвольная вершина графа. Из А начнем путь l по одному из ребер и продолжим его, проходя каждый раз по новому ребру. Все вершины графа имеют четные степени, поэтому, если есть «выход» из А, то должен быть и «вход» в А, также как и для любой другой вершины. И если есть «вход», в вершину, то должен быть и «выход». Так как число ребер конечно, то этот путь должен окончиться, причем в вершине А. Разберем на рисунке – путь l и направление его обхода видим штриховыми стрелками.
Если путь l, замкнувшийся в А, проходит через все ребра графа, то мы получим искомый эйлеровый цикл. Если остались не пройденные ребра, то должна существовать вершина В, принадлежащая l и ребру не вошедшему в l. Так как В – четная, то число ребер, которым принадлежит В и которые не вошли в путь l, тоже четно. Начнем новый путь s из В и используем только ребра, не принадлежащие l. Этот путь кончится в В. На предыдущем рисунке путь s обозначен сплошными стрелками. Объединим теперь оба цикла: из А пройдем по пути l к В, затем по циклу s и, вернувшись в В, пройдем по оставшейся части пути l обратно в А. если снова найдутся ребра, которые не вошли в путь, то найдем новые циклы. Число ребер и вершин конечно, процесс закончится. Итак, приведен алгоритм, позволяющий отыскать эйлеров цикл и показано, что он применим во всех случаях, допускаемых условиями теоремы. Таким образом, замкнутую фигуру в которой все вершины четные, можно начертить одним росчерком без повторений, начиная обводить ее с любой точки. Если граф не обладает эйлеровым циклом, то можно поставить задачу об отыскании одного эйлерового пути или нескольких эйлеровых путей, содержащих все ребра графа.
Теорема 3: Если граф обладает эйлеровым путем с концами А и В (А не совпадает с В), то граф связный, и А и В – единственные нечетные его вершины.
Доказательство. Связность графа следует из определения эйлерового пути. Если путь начинается в А, а заканчивается в другой вершине В, то и А и В- нечетные, даже если путь неоднократно проходил через А и В. В любую другую вершину графа путь должен был привести и вывести из нее, то есть все остальные вершины должны быть четными. верно и обратное. «Если граф связный и А и В единственные нечетные вершины его, то граф обладает эйлеровым путем с концами А и В». Таким образом, всякую замкнутую фигуру, имеющую в точности две нечетные вершины, можно начертить одним росчерком без повторений, начав в одной из нечетных вершин, а кончив в другой Эйлеровым графом может быть план выставки; это позволяет так расставить указатели маршрута, чтобы посетитель смог пройти по каждому залу в точности по одному разу
III. Решение задач
1).Нарисуйте граф с восемью вершинами, который: а) имеет эйлеров цикл;
б) имеет эйлеров путь;
в) не имеет ни эйлерова цикла, ни эйлерова пути;
г) имеет простой путь, содержащий все ребра графа.
2) На рисунке изображена схема зоопарка. (Вершины графа – вход, выход, перекрестки, повороты, тупики, ребра – дорожки, вдоль которых расположены клетки). Найдите маршрут, по которому экскурсовод мог бы провести посетителей, показав им всех зверей и не проходя более одного раза ни одного участка пути.
3).Сможет ли экскурсовод провести посетителей по выставке так, чтобы они побывали в каждом зале ровно один раз? Соответствующий граф приведен на рисунке; вершины графа – это вход, выход, двери, соединяющие залы, перекрестки, а ребра – залы и коридоры.
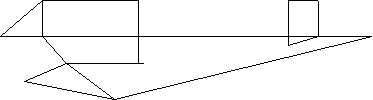
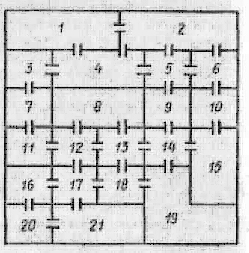
IV.Домашнее задание. На рисунке изображен план подземелья, в одной из комнат которого скрыты богатства рыцаря. После смерти рыцаря его наследники нашли завещание, в котором было сказано, что для отыскания сокровищ достаточно войти в одну из крайних комнат подземелья, пройти через все двери, причем в точности по одному разу через каждую; сокровища скрыты за той дверью, которая будет пройдена последней. В какой комнате были скрыты сокровища?