Семинар ДООМ Решение вероятностных задач с помощью построения «древа» исходов.

--Москевич Лариса Вячеславовна 16:44, 26 ноября 2007 (UZT)

Команда 061

В течение последних десятилетий элементы теории вероятностей то вводились разделом в курс математики общеобразовательной школы, то исключались вообще. Между тем, во всем мире большое внимание уделяется развитию вероятностного мышления школьника. Заслуживает внимания методика обучения учащихся теории вероятностей, которая основывается на построении «древа» исходов, она позволяет решать вероятностные задачи уже в 5-6 классах. Школьник, решающий вероятностные задачи в 5-6 классах, легче перенесет абстрактную, далекую от реальной действительности “математизацию” в старших классах. Точно также ему пойдет на пользу изучение теории вероятностей в старших классах, если уже в 5-6-х были введены некоторые элементы предмета на описательном уровне, усвоено решение задач с помощью «древа» вероятностей.

Примеры решения вероятностных задач с помощью построения «древа» исходов события.

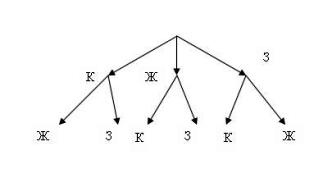
Задача №1 Из урны, где лежат красный, желтый и зеленый шары, без возвращения достают два шара наугад. Подсчитайте вероятность, что достанут желтый и зеленый шары в любой последовательности.

Решение. В каждой из двух попыток достать шар из урны возможны три исхода: е11-К, е21-Ж, е31-З; е12 – К, е22 -Ж, е32- З. Исходы второй попытки зависят от исходов первой попытки. Построим «древо» исходов урновых испытаний.

Обозначим появление желтого и зеленого шаров - событие А. Двигаясь из вершины «дерева» исходов вниз по направлениям стрелок, выберем «маршруты» (исходы совместных испытаний), в которых попадаются только условные обозначения Ж и З: е4 – (Ж,З ) и е6 – (З, Ж). Они благоприятствуют событию А. Перемножив попадающиеся на этих «маршрутах» вероятности и сложив полученные произведения, найдем, что вероятность события А равна Р(А) = ½*1/3+½*1/3 = 1/3

Ответ: 1/3.

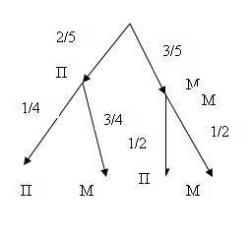
Задача №2 В игре «Морской бой» у противника осталось пять необстрелянных клеток, которые никак не соприкасаются друг с другом. На этих клетках расположены два одноклеточных корабля. Какова вероятность, что двумя выстрелами удастся «потопить» хотя бы один из них?

Решение. Проведем аналогию с урновыми испытаниями. Представим себе пустые клетки черными шарами, клетки с кораблями – белыми шарами, а квадрат, на котором они нарисованы, - урной. Выстрел – это попытка достать шар из урны. Всего в урне пять шаров – три черных и два белых. И нам фактически надо подсчитать вероятность, что из двух вынутых шаров хотя бы один окажется белым. Нам фактически надо подсчитать вероятность, что из двух вынутых шаров хотя бы один окажется белым. Эти исходы являются аналогами исходов «выстрела» - попадания (П) и промаха (М). Извлечению первым белого шара благоприятствует два исхода базового множества из пяти, а извлечению черного шара – три исхода. Поэтому вероятность попадания в первом выстреле (исход е11) равна р11 = 2/5, а вероятность промаха(исход е21- М) - р21=3/5. Исходы второго выстрела е12- П и е22- М зависят от исхода первого выстрела. В случае извлечения первым белого шара (попадания) в урне останется три черных шара и один белый шар. Поэтому условные вероятности исходов второго выстрела равны р12(е11)=1/4 и р22(е11)=3/4. Если же первым первым достанут черный шар (промах), то в урне окажутся два черных и два белых шара. Условные вероятности исходов второго выстрела в этом случае равны р12(е21) = р22(е21)=2/4=1/2. Нарисуем «древо» исходов для двух выстрелов:

Обозначим уничтожение хотя бы одного из кораблей событием А. Ему благоприятствуют три из четырех возможных «маршрутов» «дерева» исходов: е1 – (П,П), е2 – (П,М) и е3 – (М,П). Поэтому вероятность события А равна: Р(А)= 2/5*1/4+2/5*3/4+3/5*1/2 = 7/10.

Ответ: 7/10.

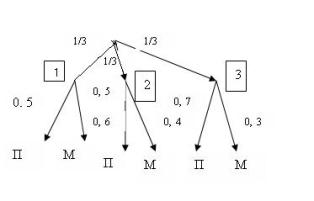
Задача №3 Трое охотников сидят в разных местах в засаде, поджидая кабана. Первый охотник может подстрелить кабана с вероятностью 0,5, второй – с вероятностью 0,6, а третий – с вероятностью 0,7. Кабан не может обежать охотников и с равными шансами может выскочить на любого из них. Подсчитайте вероятность, что охотники подстрелят кабана.

Решение. Если кабан выскакивает на одного из охотников, то охотник либо попадает в него, либо нет. Присвоим охотникам номера №1, №2, №3 и построим «Древо» исходов испытаний.

Пусть событие А означает, что охотники подстрелят кабана. Событию А благоприятствуют три «маршрута» «древа» исходов: е – (1,П), е3 – (2,П), е5 – (3,П). Поэтому кабана подстрелят с вероятностью Р(А) = 1/3*0,5+1/3*0,6+1/3*0,7=0,6.

Ответ: 0,6.

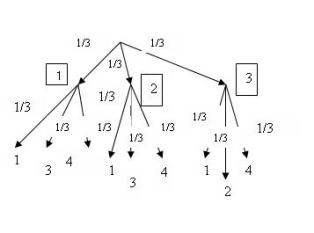
Задача №4 В урне лежат три шара с номерами один, два и три. Сначала наугад вынимают один шар и вместо него кладут в урну шар с номером четыре. Шары перемешивают и наугад достают второй шар. Подсчитайте вероятность, что сумма номеров извлеченных шаров больше четырех.

Решение. «Древо» исходов этих испытаний:

Событие А: сумма извлеченных шаров больше четырех. Событию А благоприятствует пять маршрутов древа исходов: (1,4), (2, 3), (2,4), (3,2) и (3,4). Вероятность осуществления каждого из «маршрутов» (исходов совместных испытаний) равна 1/9. Поэтому Р(А)=5*1/9=5/9.

Ответ: 5/9.

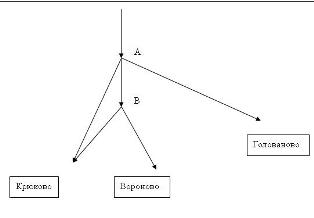
Задача №5 Турист движется по лесным тропинкам, выбирая дорогу наугад. Схема тропинок.

Подсчитайте вероятность, что он придет в село Крюково.

Решение: В сети тропинок имеются две развилки. Обозначим их буквами А и В. На развилке А турист с одинаковой вероятностью может выбрать одну из трех тропинок. Одна из них ведет прямо в Крюково. Вероятность выбора этого маршрута равна 1/3. В Крюково можно попасть также, если будет выбрана тропинка, приводящая к развилке В. На развилке В одна тропинка поворачивает в Крюково, а другая – в Вороново. Условные вероятности выбора этих тропинок равны ½. В Крюково ведут два маршрута. Вероятность попадания туриста в Крюково Р(Крюково)=1/3+1/3*1/2=1/2.

Ответ: ½.

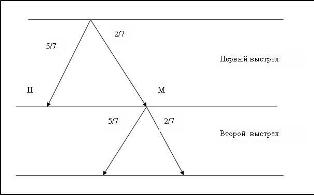
Задача №6. Вероятность стрелку одним выстрелом поразить мишень равна 5/7. Какова вероятность, что он поразит ее не более чем за два выстрела?

Решение. Событие А – попадание в мишень. «Древо» исходов двух выстрелов:

Если стрелок первым выстрелом попадает в мишень, то испытания прекращаются. Вероятность этого исхода равна 5/7. Если он промахнулся (вероятность промаха 2/7), тогда производится второй выстрел. Поражению мишени благоприятствуют маршруты «древа» исходов, приводящие к букве П. Складывая их вероятности, получим Р(А)=5/7+2/7*5/7= 45/49.

Ответ: 45/49.

Литература.

Федосеев В.Н. Решение вероятностных задач. –М.:ВШМФ «Авангард». 1999.