Семинар ДООМ Тесты по теме: "Решение задач с помощью графов"

Автор: Невзорова Марина Евгеньевна

ID команды: 002

Тесты по теме: «Решение задач с использованием графов»

Я предлагаю два варианта тестов для 5-6 классов общеобразовательных школ, лицеев. Тесты могут быть использованы учителем как контрольные или проверочные работы на внеклассных мероприятиях, на математических кружках, в играх. Тесты могут выполняться индивидуально каждым учеником, как дома, так и в классе. Тесты дают возможность учителю оперативно проверить качество усвоения как практического, так и теоретического материала с учетом индивидуальных возможностей школьников и исходя из среднего уровня подготовки класса.

Вариант1.

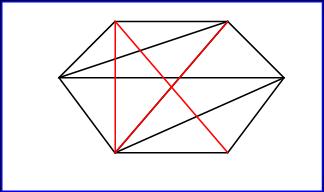
1.Встретились шестеро друзей. Каждый, здороваясь, пожал каждому руку. Сколько рукопожатий было сделано?

А) 6; Б) 12; В) 15.

2.Можно ли буквы А, Д,Е, Ж, Н русского алфавита нарисовать одним росчерком?

А) да; Б) нет; В) не знаю.

3.Сосчитай, сколько слов содержится в заклинании волшебника, если слова начинаются с букв ш или ц, второй буквой могут быть о,и,е, а оканчиваться слова могут буквами р,к,х.

А) 9; Б) 15; В) 18.

4.В первенстве класса по настольному теннису 6 участников: Андрей, Борис, Виктор, Галина, Дмитрий, Елена. Первенство проводят по круговой системе- каждый из участников играет с каждым из остальных один раз. К настоящему моменту некоторые игры уже проведены: Андрей сыграл с Борисом, Галиной, Еленой; Борис – с Андреем, Галиной; Виктор – с Галиной, Дмитрием, Еленой; Галина- с Андреем, Виктором, Борисом. Сколько игр проведено к настоящему моменту и сколько еще осталось?

А) 7; 8; Б) 6; 9; В)11; 15.

5.Докажите, что среди любых шести человек найдутся либо трое, друг с другом знакомые, либо трое, друг с другом незнакомые. Постройте граф.

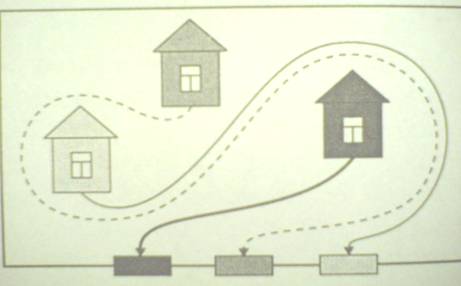
6.Во дворе, который окружен высоким забором, находятся три домика: красный, желтый и синий. В заборе есть три калитки: красная, желтая и синяя. От красного домика проведите дорожку к красной калитке, от желтого домика - к желтой калитке, от синего – к синей так, чтобы эти дорожки не пересекались. Выполните рисунок.

Вариант 2.

1.В вазе лежали конфеты четырех сортов. Каждый ребенок взял по две конфеты. И у всех оказались отличающиеся наборы конфет. Сколько могло быть детей?

А) 6; Б) 8; В) 10.

2. 2.Можно ли буквы Б, З, Р,Ф, Я русского алфавита нарисовать одним росчерком?

А) да; Б) нет; В) не знаю. 3.Шерлоку Холмсу нужно открыть сейф, для этого он должен отгадать код. Он знает, что код- это трехзначное число, составленное из цифр 7, 5,9,0, в котором нет одинаковых цифр, и меньшее числа 900. Сколько таких чисел-кодов?

А) 12; Б) 18; В) 20.

4.В пяти корзинах лежали яблоки пяти разных сортов. Яблоки первого сорта лежат в корзинах Г и Д; яблоки второго сорта – в корзинах А,Б,Г; в корзинах А,Б,В имеются яблоки пятого сорта, в корзине В имеются к тому же яблоки четвертого сорта, а в корзине Д- третьего. Пронумеруйте каждую корзину так, чтобы в корзине №1 были яблоки первого сорта; в корзине №2- второго и т.д.

А)№1 - А; №2 – Б; №3 - В; №4 - Г; №5 –Д.

Б) №1 - Д; №2 - Б; №3 - А; №4 - В; №5 - Г.

В)№1 - Г; №2 - А; №3 - Д; №4 - В; №5 – Б.

5.В компании из N человек у каждого ровно трое друзей. Доказать, что N-четное число. Постройте граф.

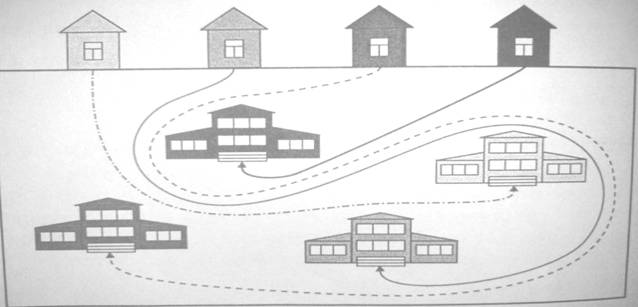
6.Четыре школьника, которые живут в желтом, зеленом, синем и красном домах, ходят в разные школы желтого, зеленого, синего и красного цвета. Однажды, на свежем снегу особенно хорошо было видно, что следы четырех мальчиков нигде не пересекают друг друга и не выходят за пределы квадрата. Возьмите карандаши и продолжите их пути так, чтобы каждый мальчик из своего дома попал в школу такого же цвета, что и его дом. Выполните рисунок.

Ответы на тест 1.

1.В. 2.нет. 3.В. 4.А 5.граф на рис.

6.рисунок

Ответы на тест 2.

1.В. 2.да. 3.А.4.В.5.Подсчитаем число пар друзей. Поскольку каждый имеет 3 друзей, т.е. входит в три такие пары, то общее число пар 3 N/2. Отсюда N – четное число. 6.рисунок