Семинар ДООМ Фрагмент урока «Применение дополнительных построений при решении задач и доказательстве теорем»

Фрагмент урока геометрии в 8-ом классе «Применение дополнительных построений при решении задач и доказательстве теорем»

Автор --Ткачук Галина Николаевна 12:33, 22 декабря 2009 (SAMT)
По мере изучения геометрии учащиеся вместе с учителем создают «шпаргалку», в которую записывают формулы, а также дополнительные построения ДП, используемые при решении задач.
ДП1. Если задана медиана в треугольнике, попробуй достроить его до параллелограмма с центром в основании медианы.

Задача. Доказать, что в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине ее длины. (достроить до прямоугольника, использовать свойства диагоналей прямоугольника).

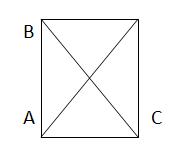
ДП2.Построение дополнительных параллельных прямых или отрезков.
Задача. Доказать, что в равнобедренной трапеции углы при основании равны.
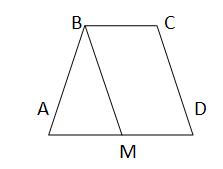ДП: ВМ||СД, ВСДМ - параллелограмм.
Задача. Доказать, что если диагонали трапеции равны, то она является равнобедренной.
Дано: АВСД- трапеция, ВС||АД, ВД=АС.
Доказать: АВ=СД.
Доказательство.
ДП: Проведем СК ||ВД до пересечения с продолжением основания АД.
ВСКД - параллелограмм. ВД=СК =АС, значит ∆АСК - равнобедренный.
Угол САК=СКА, а угол СКА= ВДА (как соответственные углы при СК||ВД и секущей АК). Значит, угол САК= углу ВДА.
Треугольник ∆АВД= ∆ДСА (по 1-ому признаку ).
Из равенства треугольников следует АВ=СД, а значит трапеция АВСД - равнобедренная.