Семинар ДООнк Урок по математике: "Первичное знакомство со скоростью сближения", 4 класс

Учитель: Мухина Наталья Викторовна.

Данный урок является уроком первичного знакомства учащихся со скоростью сближения. На представленном уроке четко и последовательно отображаются все этапы данного урока, реализуются цели и задачи. У учащихся формируется умение применять полученные знания для решения простейших задач жизненной практики. Обучение на данном уроке направлено на развитие словесно-логического мышления, абстрактного мышления, памяти, внимания, воображения, речи учащихся. Для этого были использованы таблички с числами, плакат с морскими обитателями. Дети учатся на протяжении всего урока не только самостоятельно и коллективно работать с учебником, но и анализу, и самоанализу, контролю и самоконтролю.

Тема: «Первичное знакомство со скоростью сближения»

Цели:

• Познакомить учащихся с понятием «скорость сближения» через текст задачи.

Задачи:

1.Развивать умение анализировать, сравнивать и делать выводы.

2.Развивать активность, самостоятельность.

3.Формировать умение применять полученные знания для решения простейших задач жизненной практики.

Оборудование: таблички с числами, плакат с морскими обитателями, учебник «Математика, 4 класс» И.И. Аргинской, Е.И. Ивановой.

Ход урока

I. Орг.момент

Записали число, классная работа.

II. Устный счет

1) Работа с числами.

- Какие трехзначные числа можно записать при помощи цифр 3, 2, 8, если в них не должно быть повторяющихся цифр?

На доске:

3, 2, 8

- Сколько таких чисел у вас получилось?

Дети отвечают, учитель записывает полученные числа на доске.

(328, 382, 832, 823, 283, 238).

- Сколько получится трехзначных чисел, если цифры в них могут повторяться?

(333, 323, 383, 332, 338, 233, 833, 882, 828, 883, 838, 288, 388, 222, 228, 282, 223, 232, 822, 322).

- На какие две группы можно разделить все данные числа?

(Четные и нечетные).

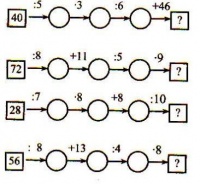
2) Работа с числовыми цепочками.

На доске:

- Какое число надо вписать в последнюю клетку цепочки?

(50, 36, 4, 40)

3) Сравнение объектов.

На доске плакат:

- Найдите длину каждого животного на плакате, если одно деление шкалы – 1 метр.

(Кит – 33 метра, акула – 15 метров, анаконда – 9 метров, крокодил – 8 метров).

- На сколько метров кит длиннее акулы? (на 18 м)

- На сколько метров крокодил короче анаконды? (на 1 метр)

4) Работа над составлением задач.

- Составьте задачи с величинами «скорость», «время», «путь» по выражениям:

а) 150 : 5;

б) 65 * 4;

в) 900 : 150;

г) 36 : 12;

Выражения записаны на доске.

- По тем же выражениям составьте задачу с величинами «стоимость товара», «цена», «количество товара».

Дети составляют задачи.

III. Постановка проблемы.

На доске записана задача:

"Длина Краснохолмского моста в москве 720 метров. Навстречу друг другу по этому мосту идут два пешехода. Скорость первого - 2 м/с, а скорость второго - 3 м/с. Какова скорость сближения?"

- Прочитайте задачу.

- Как вы думаете, что называют "скоростью сближения?"

- Зачем необходимо знать скорость сближения?

- При каком движении можно говорить о скорости сближения?

- Кто догадался, какова тема нашего урока?

IV. Новый материал.

1) Основой последующей работы является задание № 9 стр.5 учебника.

• 
• 
• 

- Прочитайте задачу. Докажите. Что это задача.

- Выполните чертеж к данной задаче.

- На сколько километров автомобили сблизятся за 1 ч пути? За 2 ч?

Расстояние, на которое сближаются движущиеся предметы в единицу времени, называют скоростью сближения.

- Какой из ответов, полученных при решении задачи, можно назвать скоростью сближения? (60 + 65 = 125 км/ч)

- На какие вопросы можно ответить, зная скорость сближения?

- Используя понятие «скорость сближения», составьте обратные задачи.

а) Навстречу друг другу выехали два автомобиля. Один ехал со скоростью 60 км/ч. С какой скоростью ехал второй автомобиль, если за 1 ч пути они сблизятся на 125 км?

б) Навстречу друг другу выехали два автомобиля. Скорость сближения равна 125 км/ч Какова скорость второго автомобиля, если первый ехал со скоростью 65 км/ч?

2) Задание 10.

- Запишите все натуральные числа, начиная с числа 7576 и кончая числом 7587.

- Разделите данные числа на две группы. Какой признак вы выделили?

- Рассмотрите, как разделили на две группы данные числа в учебнике. Какие признаки были использованы? (Юля разделила числа по количеству единиц в разряде десятков. Коля разделил на четные и нечетные).

- Допишите числа к группам, которые выделила Юля. Допишите числа к группам, которые выделил Коля.

- По каким признакам вы узнаете четные и нечетные числа?

V. Физминутка.

В ногу весело шагает

Дружный наш отряд!

На привале все устали

И присели в ряд.

К солнцу потянулись

И к земле нагнулись.

Вправо, влево наклонились

И в дальнейший путь пустились!

VI.Повторение пройденного.

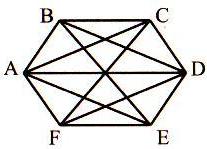
1) Задание № 11.

- Какая фигура изображена в учебнике? (Выпуклый пятиугольник).

- Какой многоугольник называется выпуклым? (Многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону.)

- Как называются отрезки АС и АD? (Диагонали).

- Какой отрезок называется диагональю?

- Сколько еще диагоналей можно провести в нем? Запишите имена. (ВЕ, ВD, СЕ)

- Сколько всего диагоналей можно провести в пятиугольнике? (Пять).

- Начертите выпуклый шестиугольник и проведите в нем все возможные диагонали. Сколько их получилось? (Девять).

- Сколько диагоналей можно провести из одной вершины пятиугольника? (Две.)

- Сколько диагоналей можно провести из одной вершины шестиугольника? (Три).

- Из одной вершины четырехугольника? (Одну.)

- Из одной вершины восьмиугольника? (Пять.)

- Из одной вершины треугольника? (Ни одной.)

Вывод. В выпуклом многоугольнике из одной вершины можно провести диагоналей на три меньше, чем вершин в данном многоугольнике.

- Объясните, почему на три меньше. (Не можем провести диагональ к данной вершине и к двум соседним вершинам.)

2) Задание 12 (1 – 3).

- Рассмотрите равенства:

ххх * 3 = ххх7

ххх * 7 = ххх3

- Какой цифрой оканчивается первый множитель в каждом равенстве? (В обоих равенствах последняя цифра первого множителя).

- У какого из этих равенств можно найти больше решений? Почему? (Больше решений будет у второго равенства, так как в нем второй множитель больше, значит, в качестве первого множителя возможно использовать меньшие числа для получения четырехзначного результата).

- Запишите несколько верных равенств, которые можно получить из данных, заменив звездочки цифрами. Запись:

339 * 3 = 1017

439 * 3 = 1317

539 * 3 = 1617

219 * 7 = 1533

319 * 7 = 2233

419 * 7 = 2933

VII. Итог урока.

- Что нового узнали на уроке?

- Что называют диагональю многоугольника?

- Что обозначает «скорость сближения»?

- Какие числа называют четными? Нечетными?

VIII. Домашнее задание.

Задание № 12 (4 – 6) по учебнику.