Системы счисления

Автор-составитель: Лысков Алексей Владимирович

Троичная система счисления.

Материал взят из Википедии — свободной энциклопедии.

Троичная система счисления — позиционная система счисления с целочисленным основанием равным 3.

Существует в двух вариантах: несимметричная и симметричная.

Троичные цифры можно обозначать любыми тремя знаками {A,B,C}, {X,Y,Z}, {!,?,%} и др., но в несимметричной троичной системе счисления чаще применяются цифры {0,1,2}, а в троичной симметричной системе счисления знаки {−,0,+}, {−1,0,+1}, {1,0,1}, {1,0,1}[1], {i,0,1}, {N,O,P}, {N,Z,P} и цифры {2,0,1}.

В цифровой электронике, независимо от варианта троичной системы счисления, одному троичному разряду (тр.р.) в троичной системе счисления соответствует один троичный триггер как минимум на трёх инверторах с логикой на входе или два двоичных триггера как минимум на четырёх инверторах с логикой на входе.

Представление чисел в троичных системах счисления

Сдвоенные комбинированные системы счисления

В сдвоенных (спаренных, комбинированных) показательных позиционных троичных системах счисления используются две системы счисления:

1. внутриразрядная система счисления с основанием a, числа которой используются для записи цифр и 2. приписная межразрядная система счисления с основанием b.

Целое число в сдвоенной показательной позиционной системе счисления представляется в виде суммы произведений значений в разрядах (цифр) — \ a_k на k-тые степени числа b: , где

   * k — число от 0 до n-1, номер числового разряда,
   * n — число разрядов,
   * a — число, основание основной внутриразрядной системы счисления,
   * ak — целые числа из множества a, называемые цифрами,
   * b — число, основание межразрядной показательной весовой функции,
   * bk — числа межразрядной функции, весовые коэффициенты разрядов.

Каждое произведение в такой записи называется (a, b)-ичным разрядом

При b=a образуются (a, a)-ичные системы счисления с произведением — akak и суммой 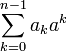, которые при a=3 превращаются в обычную (3,3)-ичную (троичную) систему счисления. При записи первый индекс часто опускается, иногда, когда есть упоминание в тексте, опускается и второй индекс.

Весовой коэффициент разряда — bk — приписной и, в общем случае, может быть необязательно показательной функцией от номера разряда — k, и необязательно степенью числа 3. Множество значений ak более ограниченно и более связано с аппаратной частью — числом устойчивых состояний триггеров или числом состояний группы триггеров в одном разряде регистра. В общем случае, ak могут быть тоже необязательно из троичного множества a={0,1,2}, но, чтобы спаренной системе быть троичной и называться троичной, как минимум, одна из двух систем должна быть троичной. Так как ak-тые ближе к аппаратной части и по ak- тым из множества a={0,1,2} или из множества a={-1,0,+1}, а не по bk мы определяем и относим число x(a, b) к троичным системам кодирования, то есть большие основания считать a основным основанием системы счисления, b в таком случае называется основанием вспомогательной системы счисления. Но и это весьма относительно, так как запись числа может быть в одной системе кодирования, а само число может быть в другой системе счисления. Пример: двоично-десятичное кодирование (BCD), в котором числа записываются в двоичном коде, а система счисления — десятичная.

Сдвоенные комбинированные троичные системы счисления

Целое число x в сдвоенной (спаренной) позиционной троичной системе записывают в виде последовательности его цифр (строки цифр), перечисляемых слева направо по убыванию старшинства разрядов:

В показательных системах счисления значениям разрядов приписываются весовые коэффициенты bk, в записи они опускаются, но подразумевается, что k-тый разряд справа налево имеет весовой коэффициент равный bk.

Из комбинаторики известно, что число записываемых кодов не зависит от основания показательной функции — b, которое определяет диапазон представляемых числами x3,b величин, и равно числу размещений с повторениями:, где:

a=3 — 3-х элементное множество a={0,1,2} из которого берутся цифры ak, n — число элементов (цифр) в числе x3,b.

Дробное число записывается и представляется в виде: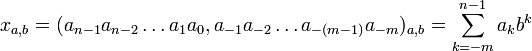 , где m — число разрядов дробной части сдвоенного (спаренного) позиционного числа справа от запятой,

при m=0 дробная часть отсутствует, число — целое,

при ak из троичного множества a={0,1,2} и b=1 образуется непозиционная троичная система счисления с одинаковыми весовыми коэффициентами всех разрядов равными 1k=1,

при ak из двоичного множества a={0,1} и b=3 в сумме будут только целые степени — 3k,

при ak из троичного множества a={0,1,2} и b=3 в сумме будут целые и удвоенные степени 3, система счисления становится обычной несимметричной троичной системой счисления, ak удовлетворяют неравенству 0<=ak<=(b-1)<b, т.е. 0<=ak<=2<3,

при ak из десятичного множества a={0,1,2,3,4,5,6,7,8,9} и b=3 в сумме будут целые степени 3 умноженные на 1, 2, 3, 4, 5, 6, 7, 8 и 9. В некоторых случаях этого может оказаться недостаточно, в таких случаях можно применить стро́енные (комтринированные), счетверённые и другие системы счисления.

Строенные комбинированные троичные системы счисления

В строенных (комтринированных) показательных позиционных троичных системах счисления используются три системы счисления. В вес разряда вводится дополнительный член в третьей системе счисления. Например, сомножитель (b/с):

В общем случае c≠3. При ak из a={0,1,2}, b=3 и c=3 образуется обычная несимметричная троичная система счисления. При a=2, b=3 и c=2 образуется (2,3,2)-ичная система счисления с дополнительным нецелочисленным весовым коэффициентом в произведении равным (3/c)=(3/2)=1,5. При других значениях a, b и c образуются другие строенные показательные позиционные системы счисления с дополнительным сомножителем (b/c), число которых бесконечно. Возможны бесконечные множества и других составных систем счисления.

Кодирование троичных цифр

Одна троичная цифра может кодироваться разными способами.

1. Трёхуровневое однопроводное кодирование:

2 — (+1) ;

1 — (0) ;

0 — (-1) .

2. Двухуровневое двухразрядное двухпроводное кодирование

1 (Binary Coded Ternary, BCT representation):

2 — (1,0);

1 — (0,1);

0 — (0,0). 3. Двухуровневое двухразрядное двухпроводное кодирование 2

(Binary Coded Ternary, BCT representation):

2 — (1,1);

1 — (0,1);

0 — (0,0).

3. Трёхразрядное одноединичное трёхпроводное кодирование 1:

2 — (1,0,0);

1 — (0,1,0);

0 — (0,0,1).

4. Трёхразрядное однонулевое трёхпроводное кодирование 2:

2 — (0,1,1);

1 — (1,0,1);

0 — (1,1,0).

5. Трёхразрядное единичное (унарное) трёхпроводное кодирование 3:

2 — (1,1,1);

1 — (0,1,1);

0 — (0,0,1).

6. Двухуровневое нулевое трёхпроводное кодирование 4:

2 — (0,0,0);

1 — (1,0,0);

0 — (1,1,0).

и др.

Сравнение с двоичной системой счисления

При поразрядном сравнении троичная система счисления оказывается более ёмкой, чем двоичная система счисления. При девяти разрядах двоичный код имеет ёмкость 29 = 512 чисел, а троичный код имеет ёмкость 39 = 19683 числа, то есть в 39 / 29 = 38,4 раза больше. При двадцати семи разрядах двоичный код имеет ёмкость 227 = 134217728 чисел, а троичный код имеет ёмкость 327 = 7625597484987 чисел, то есть в 327 / 227 = 56815,13 раз больше. При восьмидесяти одном разряде двоичный код имеет ёмкость 281 = 2417851693229258349412352 числа, а троичный код имеет ёмкость 381 = 4,434e + 38 чисел, то есть в 381 / 281 = 183396897083556,95 раз больше.

Свойства

Троичная позиционная показательная несимметричная система счисления по затратам числа знаков (в трёхразрядном десятичном числе 3*10=30 знаков) наиболее экономична из позиционных показательных несимметричных систем счисления. А. Кушнеров приписывает эту теорему Джону фон Нейману.

Перевод целых чисел из десятичной системы счисления в троичную

Для перевода целое десятичное число делят нацело с остатком (целочисленное деление) на 3 до тех пор, пока частное больше нуля. Остатки, записанные слева направо от последнего к первому являются целым несимметричным троичным эквивалентом целого десятичного числа. Пример: десятичное целое число 4810,10 переведём в несимметричное троичное целое число: число = 4810,10 делим на 3, частное = 16, остаток a0 = 0 частное = 1610,10 делим на 3, частное = 5, остаток a1 = 1 частное = 510,10 делим на 3, частное = 1, остаток a2 = 2 частное = 110,10 делим на 3, частное = 0, остаток a3 = 1 Частное не больше нуля, деление закончено. Теперь, записав все остатки от последнего к первому слева направо, получим результат 4810,10 = (a3a2a1a0)3,3 = 12103,3.

Симметричная троичная система счисления

Позиционная целочисленная симметричная троичная система счисления была предложена итальянским математиком Фибоначчи (Леонардо Пизанский) (1170—1250) для решения «задачи о гирях». Задачу о наилучшей системе гирь рассматривал Лука Пачоли (XV в.). Частный случай этой задачи был опубликован в книге французского математика Клода Баше де Мезириака «Сборник занимательных задач» в XVII веке в 1612 г. Русский перевод книги К. Г. Баше «Игры и задачи, основанные на математике» вышел в Петербурге в 1877 г. Позже этой задачей занимался петербургский академик Леонард Эйлер, интересовался Д. И. Менделеев.

Симметричность при взвешивании на рычажных весах использовали с древнейших времён, добавляя гирю на чашу с товаром. Элементы троичной системы счисления были в системе счисления древних шумеров, в системах мер, весов и денег, в которых были единицы равные 3. Но только в симметричной троичной системе счисления Фибоначчи объединены оба этих свойства.

Симметричная система позволяет изображать отрицательные числа, не используя отдельный знак минуса. Число 2 изображается цифрой 1 в разряде троек и цифрой 1 (минус единица) в разряде единиц. Число −2 изображается цифрой 1 (минус единица) в разряде троек и цифрой 1 в разряде единиц. Возможны шесть соответствий цифр (знаков) троичной симметричной системы счисления и цифр (знаков) троичной несимметричной системы счисления.

Свойства

Благодаря тому что основание 3 нечётно, в троичной системе возможно симметричное относительно нуля расположение цифр: −1, 0, 1, с которым связано пять ценных свойств:

• Естественность представления отрицательных чисел;
• Отсутствие проблемы округления.
• Таблица умножения в этой системе, как отметил О. Л. Коши, примерно в четыре раза короче.(стр.34).
• Для изменения знака у представляемого числа нужно изменять знаки у всех его цифр. Это свойство увеличивает число операций при перемене знака (в несимметричных системах изменяется только один знаковый разряд), но повышает надёжность при сбоях в одном или более разрядах.
• При суммировании большого количества чисел значение для переноса в следующий разряд растёт с увеличением количества слагаемых не линейно, а пропорционально квадратному корню числа слагаемых.
• По затратам числа знаков на представление чисел она равна троичной несимметричной системе.

Представление отрицательных чисел

Наличие положительной и отрицательной цифр позволяет непосредственно представлять как положительные, так и отрицательные числа. При этом нет необходимости в специальном разряде знака и не надо вводить дополнительный (или обратный) код для выполнения арифметических операций с отрицательными числами. Все действия над числами, представленными в троичной системе счисления с цифрами 0, 1, −1, выполняются естественно с учётом знаков чисел. Знак числа определяется знаком старшей значащей цифры числа: если она положительна, то и число положительно, если отрицательна, то и число отрицательно. Для изменения знака числа надо изменить знаки всех его цифр (то есть инвертировать его код инверсией Лукасевича). Например:

Округление

Другим полезным следствием симметричного расположения значений цифр является отсутствие проблемы округления чисел: абсолютная величина части числа, представленной отбрасываемыми младшими цифрами, никогда не превосходит половины абсолютной величины части числа, соответствующей младшей значащей цифре младшего из сохраняемых разрядов. Следовательно, в результате отбрасывания младших цифр числа получается наилучшее при данном количестве оставшихся цифр приближение этого числа, и округление не требуется.

Перевод чисел из десятичной системы в троичную

Перевод чисел из десятичной системы в троичную и соответствующий ему вопрос о гирях подробно изложены в книгах [16][17]. Там же рассказано о применении троичной системы гирь в русской практике.

Перевод в другие системы счисления

Всякое число, записанное в троичной системе счисления с цифрами 0, 1, −1, можно представить в виде суммы целых степеней числа 3, причём если в данном разряде троичного изображения числа стоит цифра 1, то соответствующая этому разряду степень числа 3 входит в сумму со знаком «+», если же цифра −1, то со знаком «-», а если цифра 0, то вовсе не входит. Это можно представить формулой

, где

- целая часть числа,

— дробная часть числа,

причём коэффициенты K могут принимать значения { 1, 0, −1 }.

Для того чтобы число, представленное в троичной системе, перевести в десятичную систему, надо цифру каждого разряда данного числа умножить на соответствующую этому разряду степень числа 3 (в десятичном представлении) и полученные произведения сложить.

Практические применения

• Работая в палате мер и весов, Д. И. Менделеев, с учётом симметричной троичной системы счисления, разработал цифровой ряд значений весов разновеса для взвешивания на лабораторных весах, который используется по сей день.
• Симметричная троичная система использовалась в советской ЭВМ Сетунь.

Интернет-ресурсы:

Википедия

traditio

Virtual Laboratory Wiki