Участник:Л.Ф. Молоткова
(→Теоретические сведения) |
|||
| Строка 1: | Строка 1: | ||
| − | Неравенства | + | Тема: Система познавательных заданий для работы с одаренными детьми, как ресурс повышения учебной мотивации в процессе изучения математики |
| + | |||
| + | Автор: [[Участник:Л.Ф. Молоткова|Л.Ф. Молоткова]] | ||
| + | |||
| + | |||
| + | <p align=right>Если человек в школе не научится творить, то и в жизни он будет только подражать и копировать | ||
| + | Л.Н. Толстой</p> | ||
| + | |||
| + | [[Изображение:mach11.jpg]] | ||
| + | |||
| + | Цели: | ||
| + | 1) расширить багаж математических знаний, получаемых на уроках; | ||
| + | 2) развивать умения и навыки учащихся ясно, связно и последовательно излагать свои мысли по теоретическим вопросам и по практическим задачам; | ||
| + | 3) развитие интереса учащихся к математике. | ||
| + | <br> | ||
| + | В работе используются пособия, разработанные и опубликованные автором ранее: | ||
| + | # [[Уравнения и неравенства с параметрами]] | ||
| + | # [[Неравенства]] | ||
| + | <br> | ||
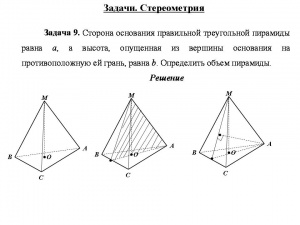
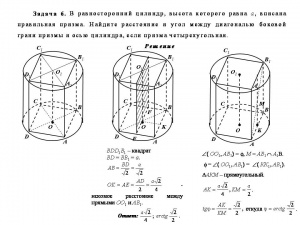
| + | В этом обзоре автор публикует задачи и решения из методического пособия для кадет "Сборник задач по геометрии | ||
| + | с решениями для подготовки кадет к математической олимпиаде среди обучающихся суворовских военных, Нахимовского военно-морского училищ и кадетских корпусов Министерства обороны Российской Федерации" | ||
| + | <br> | ||
| + | <gallery perrow=2 widths="300px" heights="300px"> | ||
| + | Изображение:mach21.jpg | ||
| + | Изображение:mach22.jpg | ||
| + | Изображение:mach23.jpg | ||
| + | Изображение:mach24.jpg | ||
| + | Изображение:mach25.jpg | ||
| + | Изображение:mach26.jpg | ||
| + | Изображение:mach27.jpg | ||
| + | Изображение:mach28.jpg | ||
| + | Изображение:mach29.jpg | ||
| + | Изображение:mach30.jpg | ||
| + | </gallery> | ||
| + | |||
<br>''учебное пособие по алгебре и началам анализа для кадет I курса (подготовка к ГИА)'' | <br>''учебное пособие по алгебре и началам анализа для кадет I курса (подготовка к ГИА)'' | ||
<br> | <br> | ||
Версия 15:45, 31 марта 2010
Тема: Система познавательных заданий для работы с одаренными детьми, как ресурс повышения учебной мотивации в процессе изучения математики
Автор: Л.Ф. Молоткова
Если человек в школе не научится творить, то и в жизни он будет только подражать и копировать Л.Н. Толстой
Цели:
1) расширить багаж математических знаний, получаемых на уроках;
2) развивать умения и навыки учащихся ясно, связно и последовательно излагать свои мысли по теоретическим вопросам и по практическим задачам;
3) развитие интереса учащихся к математике.
В работе используются пособия, разработанные и опубликованные автором ранее:
В этом обзоре автор публикует задачи и решения из методического пособия для кадет "Сборник задач по геометрии
с решениями для подготовки кадет к математической олимпиаде среди обучающихся суворовских военных, Нахимовского военно-морского училищ и кадетских корпусов Министерства обороны Российской Федерации"
учебное пособие по алгебре и началам анализа для кадет I курса (подготовка к ГИА)
- Дисциплина:
- «Математика, основы информатики и вычислительной техники»
- «Математика, основы информатики и вычислительной техники»
- Дисциплина:
по алгебре и началам анализа для кадет I курса
Тема: Неравеннства
Преподаватель: Молоткова Л. Ф.
Тема: Неравенства (подготовка к ГИА).
Учебные цели: Повторить и закрепить основные УЭ по теме.
Учебные вопросы:
- Использование свойств числовых неравенств.
- Линейные неравенства.
- Квадратные неравенства.
- Область определения выражения.
- Метод интервалов.
- Неравенства с параметром.
Решение большинства неравенств сводится к решению соответствующих уравнений. Рассмотрим решение линейных и квадратных неравенств, а также специальный метод решения неравенств – метод интервалов.
Теоретические сведения
Определение. Всякое значение неизвестного, при котором данное неравенство с неизвестным обращается в верное числовое неравенство, называется решением неравенства. Решить неравенство – значит найти все его решения или доказать, что их нет.
Определение. Неравенства вида ![]()
![]() , где a и b – некоторые действительные числа, неравные нулю, называются неравенствами первой степени, или линейными неравенствами.
, где a и b – некоторые действительные числа, неравные нулю, называются неравенствами первой степени, или линейными неравенствами.
Определение. Неравенства вида ![]()
![]() , где
, где ![]() , называют неравенствами второй степени с одним неизвестным, или квадратными неравенствами.
, называют неравенствами второй степени с одним неизвестным, или квадратными неравенствами.
(a, b, c – действительные числа)
Если a>b и b>c, то a>c. (1)
Если a>b, то и a+ c > b+ c. (2)
Если a>b и c – положительное число (c > 0), то aс>bc (3)
Если a>b и c – отрицательное число (c < 0), то aс<bc (4)
Читать полную версию