Семинар ДООМ. Решение комбинаторных задач
| (не показана 1 промежуточная версия 1 участника) | |||
| Строка 2: | Строка 2: | ||
''Автор: '''Хазова Людмила Модестовна'''''<br /> | ''Автор: '''Хазова Людмила Модестовна'''''<br /> | ||
| − | ''Команда: '''[[Участник:Многогранник 041|Многогранник]]''''' | + | ''Команда: '''[[Участник:Многогранник 041|Многогранник]]'''''<br /> |
''Другие семинары: '''[[Семинар ДООМ. Использование графов при решении задач]], [[Семинар ДООМ. Графы при решении задач]]''''' | ''Другие семинары: '''[[Семинар ДООМ. Использование графов при решении задач]], [[Семинар ДООМ. Графы при решении задач]]''''' | ||
| Строка 53: | Строка 53: | ||
==== III. '''Итог урока''' ==== | ==== III. '''Итог урока''' ==== | ||
| − | [[Категория:Проект ДООМ]] | + | [[Категория:Проект ДООМ 2007-2008 (1 цикл)]] |
Текущая версия на 15:05, 10 января 2008
Конспект урока алгебры в 8 классе.
Автор: Хазова Людмила Модестовна
Команда: Многогранник
Другие семинары: Семинар ДООМ. Использование графов при решении задач, Семинар ДООМ. Графы при решении задач
Тема: Решение комбинаторных задач
Цель: Научиться решать комбинаторные задачи с помощью графов
Содержание |
Ход урока
I. Повторение:
- Методы комбинаторики в математике, физике, химии, биологии.
- Перебор возможных вариантов.
- Дерево возможных вариантов, использование графов при решении задач.
- Комбинаторное правило умножения.
II. Решение задач:
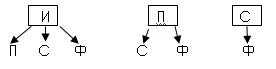
1. Из группы: Иванов, Петров, Сидоров, Федоров тренер выделил 2 человека для участия в соревнованиях. Сколько существует вариантов выбора?
3 + 2 + 1 = 6
Ответ: 6 вариантов.
2. В шахматном турнире участвуют 9 человек. Каждый из них сыграл с каждым по 1 партии. Сколько всего было сыграно партий?
8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 36
Ответ: 36 партий.
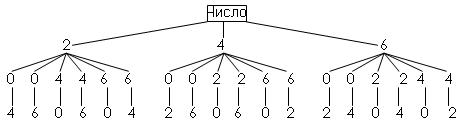
3. Из цифр 0, 2, 4, 6 составьте все возможные 3-х значные числа, в которых цифры не повторяются.
6 * 3 = 18 Ответ: 18 чисел.
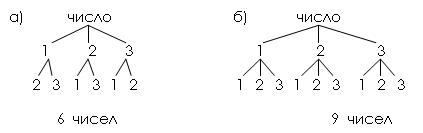
4. Из цифр 1, 2, 3 составьте все возможные 2-х заначные числа при условии, что: а) цифры в числе не повторяются; б) допускается повторение цифр в числе.
2 * 3 * 2 = 12
Ответ: 12 способов