Семинар ДООМ Волшебный квадрат
| (не показаны 11 промежуточных версий 1 участника) | |||
| Строка 1: | Строка 1: | ||
| − | <gallery caption='Из семи частей квадрата №1 составить'> | + | '''Участник:''' Молдагалиева Дамира Ароновна,IDm063 |
| − | Изображение:Кв№1.JPG| | + | |
| + | '''Тема:''' Волшебный квадрат. | ||
| + | |||
| + | '''Класс:'''5.6 | ||
| + | |||
| + | Приступая к изучению математики, наши ученики сталкиваются с огромными трудностями: им приходится решать задачи на распознавание и на построение фигур, на разбиение фигур на части и их преобразование. И все это при отсутствии геометрического опыта. Где взять этот опыт, как выработать эти навыки? И тут нам поможет дидактическая игра "Геометрический конструктор из квадрата".В основе этой работы лежат принцип игры "Танграм". | ||
| + | |||
| + | ''' Принцип игры:''' '''1.''' При складывании фигурок использовать все части-таны. '''2.'''Таны нельзя накладывать друг на друга (они могут только касаться друг друга). Фигурки, которые нужно сложить, эмоционально привлекательны для 5-6 классов. Но , чтобы сложить фигурку, нужно проявить внимание и настойчивость, аккуратность и терпение. А если фигура получилась на похожей на оригинал? Это можно поправить, переложив несколько танов. Так, играя, ученик постоянно сравнивает построенную фигуру с заданной, сравнивает углы и соотношения длин отрезков, передвигает и поворачивает фигуры. | ||
| + | |||
| + | В умелых руках любознательного ученика самый обыкновенный, хорошо всем знакомый квадрат становится волшебной фигурой. Он может, например, весь без остатка превратиться в другую фигуру или в несколько других фигур правильной или неправильной формы. Но для каждого превращения квадрат предварительно должен быть разрезан на определенные части. | ||
| + | |||
| + | |||
| + | '''Когда и как организовать эту работу в классе?''' | ||
| + | |||
| + | 1. Занятия с танграмом полезно проводить в 5-6 классах примерно 1 раз в неделю, уделяя этой работе минут 15-20 урока. | ||
| + | |||
| + | 2. Для занятий нужно сделать танграм для каждого ученика. Вырезать его можно из картона, линолеума. Хранить можно в конверте, спичечной коробке, но лучше сделать плоскую коробку-укладку в которой из танов сложен квадрат. | ||
| + | |||
| + | |||
| + | <gallery caption='Из семи частей квадрата №1 составить три квадрата, прямоугольник, параллелограмм(широкий и узкий)трапецию'> | ||
| + | Изображение:Кв№1.JPG|<center>'''Квадрат №1''' | ||
Изображение:Кв1.1.JPG| | Изображение:Кв1.1.JPG| | ||
Изображение:Кв1.2.JPG| | Изображение:Кв1.2.JPG| | ||
</gallery> | </gallery> | ||
| − | <gallery caption='Из семи частей квадрата №2 составить'> | + | <gallery caption='Из семи частей квадрата №2 составить параллелограмм, три квадрата, три параллелограмма, прямоугольник, квадрат.'> |
| − | Изображение:Кв2.JPG| | + | Изображение:Кв2.JPG|<center>'''Квадрат №2''' |
Изображение:Кв2.1.JPG| | Изображение:Кв2.1.JPG| | ||
</gallery> | </gallery> | ||
| − | <gallery caption='Из | + | <gallery caption='Из 4 частей квадрата №3 составить равнобедренный треугольник'> |
| − | Изображение:Кв3.JPG| | + | Изображение:Кв3.JPG|<center>'''Квадрат №3''' |
Изображение:Кв3.1.JPG| | Изображение:Кв3.1.JPG| | ||
| − | |||
</gallery> | </gallery> | ||
| − | <gallery caption='Из | + | <gallery caption='Из 4 частей квадрата №4 составить прямоугольный треугольник.'> |
| − | Изображение:Кв4.JPG| | + | Изображение:Кв4.JPG|<center>'''Квадрат№4''' |
Изображение:Кв4.1.JPG| | Изображение:Кв4.1.JPG| | ||
</gallery> | </gallery> | ||
| − | <gallery caption='Из | + | <gallery caption='Из 5 частей квадрата №5 составить шестиугольник'> |
| − | Изображение:Кв5.JPG| | + | Изображение:Кв5.JPG|<center>'''Квадрат№5''' |
Изображение:Кв5.1.JPG| | Изображение:Кв5.1.JPG| | ||
</gallery> | </gallery> | ||
| − | <gallery caption='Из семи частей квадрата №6 составить'> | + | <gallery caption='Из семи частей квадрата №6 составить правильный пятиугольник.'> |
| − | Изображение:Кв6.JPG| | + | Изображение:Кв6.JPG|<center>'''Квадрат №6''' |
Изображение:Кв6.1.JPG| | Изображение:Кв6.1.JPG| | ||
</gallery> | </gallery> | ||
| − | <gallery caption='Из | + | <gallery caption='Из 11 квадратов требуется составить один квадрат. '> |
| − | + | ||
Изображение:Кв7.3.JPG| | Изображение:Кв7.3.JPG| | ||
| + | Изображение:Послед.JPG|<center>'''Квадрат №7''' | ||
</gallery> | </gallery> | ||
| − | <gallery caption='Из семи частей квадрата №8 составить'> | + | <gallery caption='Из семи частей квадрата №8 составить прямоугольник, параллелограмм, трапецию, ромб,квадрат.'> |
| − | Изображение:Кв8.JPG| | + | Изображение:Кв8.JPG|<center>'''Квадрат №8''' |
Изображение:Кв8.1.JPG| | Изображение:Кв8.1.JPG| | ||
</gallery> | </gallery> | ||
| − | <gallery caption='Из семи частей квадрата №9 составить'> | + | <gallery caption='Из семи частей квадрата №9 составить прямоугольник, равносторонний треугольник.'> |
| − | Изображение:Кв9.JPG| | + | Изображение:Кв9.JPG|<center>'''Квадрат№9''' |
Изображение:Кв9.1.JPG| | Изображение:Кв9.1.JPG| | ||
</gallery> | </gallery> | ||
| − | <gallery caption='Из семи частей квадрата №10 составить'> | + | <gallery caption='Из семи частей квадрата №10 составить два равносторонних треугольника.'> |
| − | Изображение:Кв10.JPG| | + | Изображение:Кв10.JPG|<center>'''Квадрат №10''' |
Изображение:Кв10.1.JPG| | Изображение:Кв10.1.JPG| | ||
</gallery> | </gallery> | ||
| − | <gallery caption='Из семи частей квадрата №11 составить'> | + | <gallery caption='Из семи частей квадрата №11 составить три равных равносторонних треугольника.'> |
| − | Изображение:Кв11.JPG| | + | Изображение:Кв11.JPG|<center>'''Квадрат №11''' |
Изображение:Кв11.1.JPG| | Изображение:Кв11.1.JPG| | ||
| + | |||
| + | </gallery><gallery caption='Из частей главных квадратов придумать фигуры'> | ||
| + | Изображение:Гот1.JPG|<center>'''Елочка и снегурочка'''</center> | ||
| + | Изображение:Гот3.JPG|<center>'''Кораблик'''</center> | ||
| + | Изображение:Гот4.JPG|<center>'''Собачка'''</center> | ||
| + | Изображение:Гот5.JPG|<center>'''Кошка'''</center> | ||
</gallery> | </gallery> | ||
| + | |||
| + | [[Категория:Проект ДООМ 2009-2010]] | ||
Текущая версия на 06:28, 9 декабря 2009
Участник: Молдагалиева Дамира Ароновна,IDm063
Тема: Волшебный квадрат.
Класс:5.6
Приступая к изучению математики, наши ученики сталкиваются с огромными трудностями: им приходится решать задачи на распознавание и на построение фигур, на разбиение фигур на части и их преобразование. И все это при отсутствии геометрического опыта. Где взять этот опыт, как выработать эти навыки? И тут нам поможет дидактическая игра "Геометрический конструктор из квадрата".В основе этой работы лежат принцип игры "Танграм".
Принцип игры: 1. При складывании фигурок использовать все части-таны. 2.Таны нельзя накладывать друг на друга (они могут только касаться друг друга). Фигурки, которые нужно сложить, эмоционально привлекательны для 5-6 классов. Но , чтобы сложить фигурку, нужно проявить внимание и настойчивость, аккуратность и терпение. А если фигура получилась на похожей на оригинал? Это можно поправить, переложив несколько танов. Так, играя, ученик постоянно сравнивает построенную фигуру с заданной, сравнивает углы и соотношения длин отрезков, передвигает и поворачивает фигуры.
В умелых руках любознательного ученика самый обыкновенный, хорошо всем знакомый квадрат становится волшебной фигурой. Он может, например, весь без остатка превратиться в другую фигуру или в несколько других фигур правильной или неправильной формы. Но для каждого превращения квадрат предварительно должен быть разрезан на определенные части.
Когда и как организовать эту работу в классе?
1. Занятия с танграмом полезно проводить в 5-6 классах примерно 1 раз в неделю, уделяя этой работе минут 15-20 урока.
2. Для занятий нужно сделать танграм для каждого ученика. Вырезать его можно из картона, линолеума. Хранить можно в конверте, спичечной коробке, но лучше сделать плоскую коробку-укладку в которой из танов сложен квадрат.
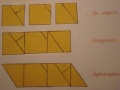
- Из семи частей квадрата №1 составить три квадрата, прямоугольник, параллелограмм(широкий и узкий)трапецию
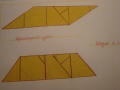
- Из семи частей квадрата №2 составить параллелограмм, три квадрата, три параллелограмма, прямоугольник, квадрат.
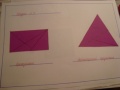
- Из 4 частей квадрата №3 составить равнобедренный треугольник
- Из 4 частей квадрата №4 составить прямоугольный треугольник.
- Из 5 частей квадрата №5 составить шестиугольник
- Из семи частей квадрата №6 составить правильный пятиугольник.
- Из 11 квадратов требуется составить один квадрат.
- Из семи частей квадрата №8 составить прямоугольник, параллелограмм, трапецию, ромб,квадрат.
- Из семи частей квадрата №9 составить прямоугольник, равносторонний треугольник.
- Из семи частей квадрата №10 составить два равносторонних треугольника.
- Из семи частей квадрата №11 составить три равных равносторонних треугольника.
- Из частей главных квадратов придумать фигуры