Копилка знаменитых задач продолжение
| Строка 37: | Строка 37: | ||
Ответ: 8 футов или ~ 244 см. | Ответ: 8 футов или ~ 244 см. | ||
| − | [[Изображение:Индийская_задача.JPG]] | + | [[Изображение:Индийская_задача.JPG|400x200px]] |
'''''2.Решение древнекитайской задачи''''' | '''''2.Решение древнекитайской задачи''''' | ||
| Строка 73: | Строка 73: | ||
х + у = 35 | х + у = 35 | ||
| − | + | ||
| − | + | ||
2х + 4у = 94. | 2х + 4у = 94. | ||
Умножим все члены уравнения на 2 и вычтем первое уравнение из второго. | Умножим все члены уравнения на 2 и вычтем первое уравнение из второго. | ||
| Строка 103: | Строка 102: | ||
Сделаем рисунок: | Сделаем рисунок: | ||
| − | [[Изображение:Пифагор.JPG]] | + | [[Изображение:Пифагор.JPG|400x200px]] |
Расстояние от основания более высокой пальмы до места появления рыбы, обозначим основания х. тогда расстояние до более низкой пальмы (50-х) локтей, т.к. известно расстояние между ними – 50 локтей. | Расстояние от основания более высокой пальмы до места появления рыбы, обозначим основания х. тогда расстояние до более низкой пальмы (50-х) локтей, т.к. известно расстояние между ними – 50 локтей. | ||
| Строка 161: | Строка 160: | ||
Зная, что ещё цветков получил уважаемый учитель, составим уравнение: | Зная, что ещё цветков получил уважаемый учитель, составим уравнение: | ||
| − | [[Изображение:Дроби.JPG]] | + | [[Изображение:Дроби.JPG|400x200px]] |
Ответ: 120 цветков. | Ответ: 120 цветков. | ||
| Строка 213: | Строка 212: | ||
Служившему воину дано вознаграждение за первую рану 1 копейка, за другую -2 копейки, за третью – 4 копейки и т.д. По исчислению нашлось , что воин получил всего вознаграждения 655 руб. 35 коп. Спрашивается число его ран. | Служившему воину дано вознаграждение за первую рану 1 копейка, за другую -2 копейки, за третью – 4 копейки и т.д. По исчислению нашлось , что воин получил всего вознаграждения 655 руб. 35 коп. Спрашивается число его ран. | ||
| − | [[Изображение:Задача_воин.JPG]] | + | [[Изображение:Задача_воин.JPG|400x200px]] |
| − | [[Изображение:Индусская_задача.JPG]] | + | [[Изображение:Индусская_задача.JPG|400x200px]] |
'''''9. Задача Эйлера''''' | '''''9. Задача Эйлера''''' | ||
| Строка 227: | Строка 226: | ||
Пусть у первой крестьянки x яиц, тогда у второй 100 – x. Если бы первая имела 100 – x яиц, она выручила бы, мы знаем 15 крейцеров. Значит, первая крестьянка продала яйца по цене | Пусть у первой крестьянки x яиц, тогда у второй 100 – x. Если бы первая имела 100 – x яиц, она выручила бы, мы знаем 15 крейцеров. Значит, первая крестьянка продала яйца по цене | ||
| − | [[Изображение:Задача_Эйлера.JPG]] | + | [[Изображение:Задача_Эйлера.JPG|400x200px]] |
Отрицательный корень в данном случае не имеет смысла; у задачи – только одно решение: первая крестьянка принесла 40 яиц и , значит, вторая 60. | Отрицательный корень в данном случае не имеет смысла; у задачи – только одно решение: первая крестьянка принесла 40 яиц и , значит, вторая 60. | ||
| Строка 233: | Строка 232: | ||
Предположим, что вторая крестьянка имела в k раз больше яиц, чем первая. Выручили они одинаковые суммы; это значит, что первая крестьянка продавала свои яйца в k раз дороже , чем вторая. Если бы перед торговлей они поменялись яйцами , то первая крестьянка имела бы в k раз больше яиц , чем вторая , и продавала бы их в k раз дороже. Это значит ,что она выручила бы в k больше денег, чем вторая. Следовательно, имеем: | Предположим, что вторая крестьянка имела в k раз больше яиц, чем первая. Выручили они одинаковые суммы; это значит, что первая крестьянка продавала свои яйца в k раз дороже , чем вторая. Если бы перед торговлей они поменялись яйцами , то первая крестьянка имела бы в k раз больше яиц , чем вторая , и продавала бы их в k раз дороже. Это значит ,что она выручила бы в k больше денег, чем вторая. Следовательно, имеем: | ||
| − | [[Изображение:Задача_Эйлера_1.JPG]] | + | [[Изображение:Задача_Эйлера_1.JPG|400x200px]] |
'''''10. Покупка лошади''''' | '''''10. Покупка лошади''''' | ||
| Строка 248: | Строка 247: | ||
Решение | Решение | ||
| − | [[Изображение:Покупка_лошади.JPG]] | + | [[Изображение:Покупка_лошади.JPG|400x200px]] |
Версия 16:54, 24 октября 2008
Посмотреть страницу Копилка знаменитых задач. Если вы увидите сообщение что количество опубликованных знаков превышает длину страницы, то вы можете разместить свои задачи на странице Копилка знаменитых задач продолжение 3
Задачи участников ДООМ
ЛАДА-ВЕКТОР
1. Задача индийского математика XII в. Бхаскары.
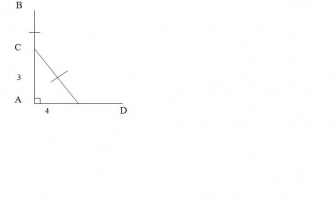
На берегу реки рос тополь одинокий. Вдруг порыв ветра его ствол надломил. Бедный тополь упал. И угол прямой с теченьем реки его ствол составлял. Запомни теперь, что в том месте река в четыре лишь фута была широка. Верхушка склонилась у края реки. Осталось три фута всего от ствола. Прошу тебя, скоро теперь мне скажи: У тополя как велика высота?
Решение:
Дано:
треугольник ACD – прямоугольный,
АС = 3 фута,
AD = 4 фута.
Найти: АВ.
Решение:
АВ = АС + СD; ВС = СD;
CD 2 = AC x2 + AD x2 (по теореме Пифагора),
CD x2 = 3 x2 + 4 x2, CD x2 = 25, CD = 5 (Ф);
АВ = 3+5 = 8 (Ф).
1 фут (1 Ф) ~ 30,5 см.
Ответ: 8 футов или ~ 244 см.
2.Решение древнекитайской задачи
В клетке находятся фазаны и кролики. Известно, что у них 35 голов и 94 ноги. Узнайте число фазанов и число кроликов.
Решение:
I способ Так решали в древнем Китае.
Представим, что наверх клетки, в которой сидят фазаны и кролики, мы положим морковь. Все кролики встанут на задние лапки, чтобы дотянуться до моркови!
1) Сколько ног в этот момент будет стоять на земле?
35 2=70 (ног).
2) Но в условии даны 94 ноги, где же остальные? Это передние лапы кроликов:
94 – 70= 24.
3) Сколько же кроликов?
24: 2 = 12.
4) Сколько фазанов?
35 – 12 = 23.
Ответ: 12 кроликов и 23 фазана.
II способ решения:
Пусть х – число фазанов, у – число кроликов. Всего у них 35 голов и 94 ноги. Значит,
х + у = 35
2х + 4у = 94. Умножим все члены уравнения на 2 и вычтем первое уравнение из второго.
2х + 2у = 70
2х + 4у = 94
2у = 24
у = 12
В клетке было 12 кроликов.
х = 35 – у
х = 23
Было 23 фазана.
Ответ: 23 фазана и 12 кроликов.
3. Задача на применение теоремы Пифагора (Арабский математик XI век)
На обоих берегах реки растет по пальме, одна против другой. Высота одной-30 локтей, другой -20 локтей; расстояние между их основаниями- 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, всплывшую к поверхности воды между пальмами; обе кинулись к ней разом и достигли её одновременно. На каком расстоянии от основания более высокой пальмы появилась рыба?
Решение:
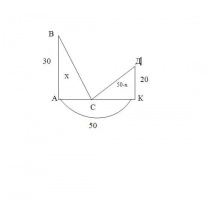
Расстояние от основания более высокой пальмы до места появления рыбы, обозначим основания х. тогда расстояние до более низкой пальмы (50-х) локтей, т.к. известно расстояние между ними – 50 локтей.
Рассмотрим прямоугольные треугольники: ABC и KDC.
АВ= 30 локтей, КД= 20 локтей, АС= х локтей, КС=(50-х) локтей, ВС=ДС, т.к. птицы достигли рыбы одновременно.
Применяя теорему Пифагора.
АВ x2 +АС x2 = ВС x2 и КД x2 +КС x2 =ДС x2, т.к. ВС=ДС, то ВС x2 =КД x2 +КС; x2 30 x2 +х =20 x2 +(50-х) x2; 900+х x2 =400+2500-100х+х x2; х=20 Ответ: 20 локтей.
4.Задача на числа (Диофант, III в.)
Найдите 2 числа, зная, что их сумма равна 20, а произведение 96.
1 способ решения:
Первое число обозначим х, второе у и составим систему уравнений; т.к. сумма чисел равна 20, то: х + у = 20; произведение 96, то х у = 96, т.е
Используя т.Виета:
х = 12; у = 8 или х =18; у = 12.
Ответ: 8 и 12.
2 способ решения:
Первое число обозначим х, второе (20-х), т.к. сумма чисел равна 20. Зная их произведение, составим уравнение:
х (20-х) = 96; х -20х+ 96 = 0
Используя т.Виета:
х=8
х=12.
Ответ: 8 и 12.
5.Задача на дроби (Бхаскары; Индия,XII в.)
Из множества чистых цветков лотоса были принесены в жертвы: Шиве- 3 доля этого множества; Вишну-пятая и Солнца- шестая; четвертую долю получил Бхавани, а остальные шесть цветков получил уважаемый учитель. Сколько было цветков?
Решение:
Пусть всего цветов было х.
Шива получил третью долю из всего множества, т. е. 1х/4.
Зная, что ещё цветков получил уважаемый учитель, составим уравнение:
Ответ: 120 цветков.
6.Задача на составление системы уравнений (Старинная задача).
Лошадь вместе с седлом стоит 235 рублей; лошадь же вместе со с рубей стоит 250 рублей; сбруя же с седлом стоит 135 рублей. Что стоит лошадь, что седло, что сбруя?
Решение:
Решим задачу с помощью системы уравнений. Пусть х
Возьмём за х рублей стоимость лошади, у рублей – сёдла, я рублей – сбруи. По условию:
x+y=235;
x+y=250;
y+z=135;
Вычитаем из первого уравнения второе:
x+y-x-z=235-250;
y=z-15;
Подставим полученное выражение в третье уравнение:
z-15+z=135;
z=75;
Найдём у:
у = z- 15=75-15=60;
Найдём х:
х + 60=235;
х=175.
Ответ: 175 рублей, 60 рублей, 75 рублей.
7.Вознаграждение воина.
Задача из «Полного курс чистой математики , сочиненный Артиллерии Штык-Юнкером и Математики партикулярным Учителем Ефимом Войтяховским в пользу и употребление юношества и упражняющихся в Математике» (1795г)
Служившему воину дано вознаграждение за первую рану 1 копейка, за другую -2 копейки, за третью – 4 копейки и т.д. По исчислению нашлось , что воин получил всего вознаграждения 655 руб. 35 коп. Спрашивается число его ран.
9. Задача Эйлера
Две крестьянки принесли на рынок вместе 100 яиц, одна больше, нежели другая; обе выручили одинаковые суммы. Первая сказала тогда второй: «Будь у меня твои яйца, я выручила бы 15 крейцеров». Вторая ответила: «А будь твой яйца у меня, я выручила бы за них крейцера». Сколько яиц у каждой?
РЕШЕНИЕ
I способ:
Пусть у первой крестьянки x яиц, тогда у второй 100 – x. Если бы первая имела 100 – x яиц, она выручила бы, мы знаем 15 крейцеров. Значит, первая крестьянка продала яйца по цене
Отрицательный корень в данном случае не имеет смысла; у задачи – только одно решение: первая крестьянка принесла 40 яиц и , значит, вторая 60. II способ: Предположим, что вторая крестьянка имела в k раз больше яиц, чем первая. Выручили они одинаковые суммы; это значит, что первая крестьянка продавала свои яйца в k раз дороже , чем вторая. Если бы перед торговлей они поменялись яйцами , то первая крестьянка имела бы в k раз больше яиц , чем вторая , и продавала бы их в k раз дороже. Это значит ,что она выручила бы в k больше денег, чем вторая. Следовательно, имеем:
10. Покупка лошади
Задача из «Арифметики» Магницкого.
Некто продал лошадь за 156 руб. Но покупатель, приобретая лошадь, раздумал её покупать и возвратил продавцу, говоря - Нет мне расчёта покупать за эту цену лошадь, которая таких денег не стоит тогда продавец предложил другие условия. Если, по-твоему цена лошади высока, то купи только её подковные гвозди, лошадь же получишь тогда в придачу бесплатно. Гвоздей в каждой подкове 6. За первый гвоздь дай мне всего ¼ коп., за второй – ½ коп., за третий – 1 коп. и т.д. Покупатель соблазнённый низкой ценой и желая даром получить лошадь, принял условия продавца, рассчитывая, что за гвозди придётся уплатить не более 10 рублей. На сколько покупатель проторговался?
Решение
--Лада-Вектор ID 279 15:40, 24 октября 2008 (SAMST)
--Сталкера задач ID 219 16:11, 24 октября 2008 (SAMST)
Задача 1. Вопросил некто некоего учителя: "Сколько имеешь учеников у себя,так как хочу отдать сына к тебе в училище". Учитель ответил: "Если ко мне придет учеников еще столько же, сколько имею, и полстолько, и четвертая часть, и твой сын, тогда будет у меня учеников 100." Сколько было у учителя учеников?
Решение:
2х+1/2*х+1/4*х+1=100, х=36
Ответ: 36 учеников.
ЗВЕЗДА ID 248
ЗАДАЧИ РАЗНЫХ СТРАН
Задача №1 РОССИЯ
На вопрос о том, сколько времени, был дан такой ответ: «Две пятых времени, прошедшего от полуночи до этого момента, равно двум третьим времени, которое осталось до полудня». Сколько сейчас времени?
Решение
От полуночи до полудня 12 часов, если t ч. — время, прошед¬шее от полуночи до настоящего времени, то:
2 / 3t = 2 / 3(12 − t)
Следовательно, в данный момент t = 7,5 ч., т.е. часы показы¬вают 7 ч. 30 мин. Ответ: 7 ч. 30 мин.
Задача №2 ФРАНЦИЯ
Чему равно наименьшее число, которое при делении на 2, 3, 4, 5, 6 дает в остатке 1, 2, 3, 4, 5 соответственно.
Решение:
Пусть п - неизвестное число. Так как при делении п на 2 в остатке 1, значит, (п + 1) делится на 2 без остатка. Если п при делении на 3 дает в остатке 2, то число (п + 1) делится на 3 без остатка и т.д. Наименьшее кратное 2, 3, 4, 5, 6 равно 60. Сле¬довательно, п = 60 -1 = 59.
Ответ: 59.
Задача №3
Когда у старушки Леони спрашивают, сколько у нее кошек, она меланхолично отвечает: «Четыре пятых моих кошек плюс четыре пятых кошки». Сколько же у Леони кошек?
Решение:
Пусть п - число кошек у Леони. Со слов старушки можем записать уравнение:
4 4 — n + - = n 5 5
n = 4
Ответ: 4 кошки.
Задача №4 БОЛГАРИЯ
Отец, по имени Николай, с сыном и отец, по имени Петр, с сы¬ном отправились удить рыбу. Число рыб, пойманных Николаем, оканчивается на 2, а число рыб, пойманных его сыном - на 3; число рыб, пойманных Петром, также оканчивается на 3, а число рыб, пойманных его сыном - на 4. Число рыб, пойманных на¬шими рыболовами вместе, совпадает с квадратом некоторого натурального числа. Как зовут сына Николая?
Решение:
Так как сумма последних цифр 2 + 3 + 3 + 4 = 12 оканчива¬ется на 2, и не существует квадрата натурального числа, который оканчивается на 2, то речь идет не о четырех, а лишь о трех ры¬баках, т.е. сын одного из любителей рыбной ловли одновременно является отцом другого (2 + 3 + 4 = 9). Николай не может быть сыном Петра, т.к. улов Николая оканчивается на 2, а не на 4, как того требует условие задачи. Следовательно, Петр - сын Николая.
Ответ: Петр.
Задача №5 ДАНИЯ
Рыбаки Адам, Бауэр, Кристиансен и Дазе (сокращенно: А, Б, К, Д), взвесив свой улов, установили следующее:
1) Д поймал больше, чем К; 2) А и Б вместе поймали столько же, сколько К и Д вместе; 3) А и Д вместе поймали меньше, чем Б а К вместе. Расположите результаты взвешиваний уловов а, б, к, д рыба¬ков А, Б, К, Д по величине.
Решение:
Результаты взвешивания улов а, б, к, д удовлетворяют соот¬ношениям: к<д (1)
а + б = к + д (2)
а + д < б + к (3)
Из (2) и (3) при сложении получим неравенство:
2а + б + д < б + 2к + д
2а < 2к
а < к (4)
Из (1) и (4) следует, что а < к < д.
Из (2) и (4) получим д < б. Значит, выполняется цепочка не¬равенств: а < к < д < б. Значит, самый большой улов у Бауэра, за ним у Дазе, Кристиансена и Адама.
Задача №6 АВСТРАЛИЯ
Скотовод завещал трем своим сыновьям Альфреду, Джону и Чарльзу разделить стадо овец следующим образом: Альфред получит на 20% больше Джона и на 25% больше Чарльза. Часть Джона - 3600 овец. Сколько овец получит Чарльз?
Решение:
Альфред получит 3600 + 0,2 • 3600 = 4320 овец. Это число на 25% больше z - числа овец Чарльза, т.е.
4320 = z - 0,25z
z = 3456
Ответ: 3456 овец получит Чарльз.
Задача №7 ЧЕХИЯ
По преданию, основательница чешского государства принцес¬са Либуша обещала отдать свою руку тому из трех женихов, кто сумеет решить задачу: «Если бы я дала первому жениху половину слив из этой корзины и еще одну сливу, второму жениху - поло¬вину оставшихся слив и еще одну сливу, а оставшиеся сливы поделила пополам и половину их и еще три сливы дала бы треть¬ему жениху, то корзина бы опустела». Сколько слив в корзине?
Ответ: 22 сливы.
--ЗВЕЗДА ID 248--ЗВЕЗДА ID 248 16:55, 24 октября 2008 (SAMST)